曲线拟合
No.1
什么是曲线拟合
所谓的曲线拟合,就是使用某一个模型(或者称为方程式),将一系列的数据拟成平滑的曲线,以便观察两组数据之间的内在联系,了解数据之间的变化趋势。
No.2
曲线拟合的应用
在数据分析时,我们有时需要通过已有数据来预测未来数据。在一些复杂的数据模型中,数据维度很多,数据之间的关系很复杂,我们可能会用到深度学习的算法。但是在一些简单的数据模型中,数据之间有很明显的相关性,那我们就可以使用简单的曲线拟合来预测未来的数据。
No.3
模型的优化
根据模型的建立与求解的过程中, 发现拟合的函数表达式有很多, 即使根据可决系数, 显着性检验和系数值稳定等条件, 依然会出现多个表达式。那么这种情况是要选择优化数据和处理, 根据实际情况而处理。函数表达式的系数也决定了函数的灵敏度, 选择原则在不同的问题中根据数据最终结果来处理。
No.4
曲线拟合的方法
Excel曲线工具
假设我们有一组用户生命周期价值(LTV)和天数的对应数据
DayLTV1$0.202$0.353$0.454$0.525$0.576$0.607$0.628$0.63
将数据放进Excel中,插入折线图
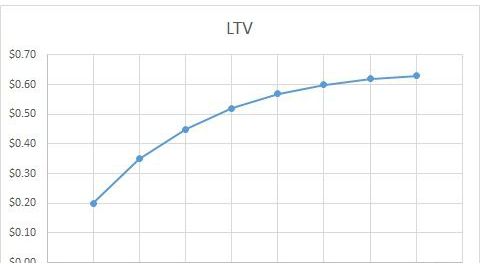
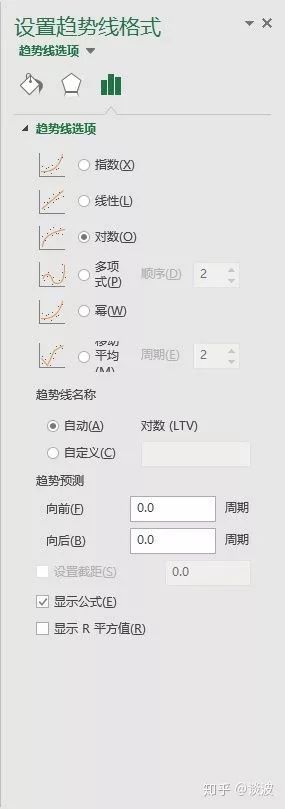
右击蓝色曲线,选择“添加趋势线”,并选择趋势线为“对数”,并勾选“显示公式”
可以看到,曲线图中出现了一条虚线的曲线,并显示了对应的公式为
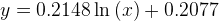
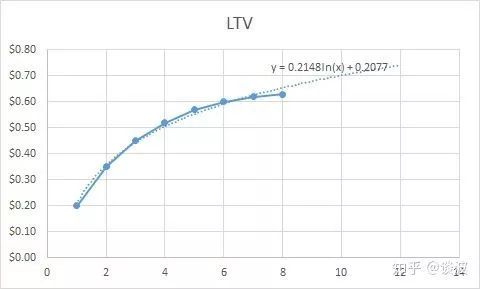
Excel的趋势线工具提供了几个常用的函数,包括指数函数、对数函数等,可以满足一般需求。但是如果数据曲线相对复杂的话,就需要用到下面的工具了。
介绍一个非常好用的在线曲线拟合工具:
http://www.qinms.com/webapp/curvefit/cf.aspx
No.5
Python matplotlib库
Python的matplotlib库有一个自定义公式来拟合曲线的功能。下面代码演示了通过它来拟合上述例子的过程
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import scipy.optimize as optimization
data_day = [1,2,3,4,5,6,7,8] #x坐标值|x coord
data_ltv = [0.2,0.35,0.45,0.52,0.57,0.6,0.62,0.63] #y坐标值|y coord
xdata = np.array(data_day)
ydata = np.array(data_ltv)
#定义使用的公式|customize equation
def lnFunction(x, A, B):
return A*np.log(x)+B
guess = [1, 1] #定义初始A、B|initialize a and b
try:
params, params_covariance = optimization.curve_fit(lnFunction, xdata, ydata, guess) #拟合,A、B结果存入params|curve fitting and store a, b values to params
print params
result = '' #输出结果|to store result
for i in range(1, 15):
result += str(round(lnFunction(i, params[0], params[1]), 2)) #将i带入公式中的x,使用拟合出的A、B值计算y值,并保留两位小数|calculate result for each i as x using the a, b values, and round the result to 2 points
if i != 14:
result += ',' #每个结果用逗号隔开,并省略最后一个逗号|separate each result with comma, and omit the last comma
print result
except:
print ''
输出结果为:
[0.21482987 0.20772681]
0.21,0.36,0.44,0.51,0.55,0.59,0.63,0.65,0.68,0.7,0.72,0.74,0.76,0.77
No.6
曲线拟合公式
在前面的例子中,我们使用了对数函数来进行拟合。在上文提到的在线曲线拟合工具网站中,也列出了一些常见的拟合方程,包括直线、多项式、对数、指数等。其中有一个方程对于拟合自然曲线非常好用,就是四参数方程。
四参数方程的格式为:
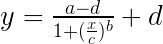
最后
统计学作为一门新兴的学科, 在未来的社会发展中有着举足轻重的意义。拟合方法是一种可以很好的查看出数据趋势的一种方法,同样也可以用在数据近似,差值等方法中。使得数学建模的操作增添新的工具, 极大地提高了数据分析的科学性。


文案:竞赛部 董聿铭
排版:张添娇 高歆然
审核:由 月 李天娇





服务控制及优化启动过程)













