一、数
1.1 整数类型( 十、二、八、十六进制 )
python中整数类型与数学中的整数概念一致，有正有负，取值任意。
整数的表示形式：
整数类型表示形式举例十进制34,163,210
二进制0b1101 或 0B1101
八进制0o357 或 0O357
十六进制0x45ac 或 0X45ac
1.2 浮点数类型( round()、科学计数法表示 )
python中浮点数即指带有小数点和小数的数字，浮点数取值范围(-10308至10308)和小数精度(10-16)都存在限制(这些限制对于常规运算可以忽略)。
浮点数间运算存在不确定尾数，这不是bug。
原因在于计算机中是以有限位数的二进制表示小数的，二者可以无限接近但不完全相同，这就使得计算机以二进制形式计算小数运算时存在了误差，在输出时计算机再截取一定的小数位数输出，就可能产生尾数。python中不确定尾数一般发生在10-16左右。
例如：
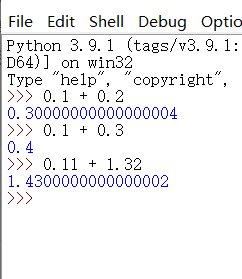
图1-1 浮点数间运算的不确定尾数
图1-1中，(0.1 + 0.2) 和 (0.11 + 1.32) 的结果不等于正确结果的情况即为出现不确定尾数。
rang()函数辅助解决不确定尾数问题 round(x, d)对x四舍五入，d是小数截取位数
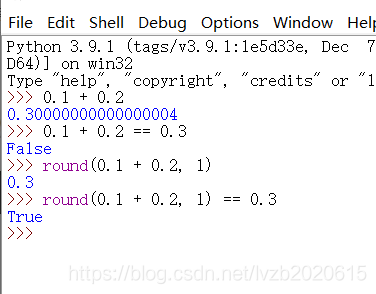
图1-2 round()函数四舍五入
浮点数的科学计数法表示形式
科学计数法表示使用字母e或E作为幂的符号，以10为基数，格式如下：
浮点数科学计数法表示形式0.6356.35e-1
51.064155.106415E1
-0.413-4.13E-1
-165.333-1.65333e2
1.3 复数类型( 多用于空间变换或复变函数相关，虚实部的获取 )
在数学中，a + bj被称为复数，其中a是实部，b是虚部，j是复数单位。
在python中，复数与数学中的复数相同。
.real获得复数的实部
.imag获得复数的虚部
例如：
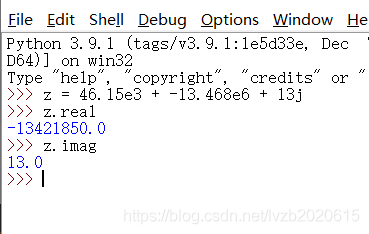
图1-3 python中的复数即获取虚实部
二、数值运算操作符( 加、减、乘、除、模、幂、整数除、取相反数 )
2.1 常用操作符
操作符及使用说明x + y加，求x与y的和
x - y减，求x与y的差
x * y乘，求x与y的积
x / y除，求x与y的商(浮点数结果)。10 / 3 结果为3.3333333333333335
x // y整数除，求x与y的商(整数结果)。10 // 3 结果为3
+ x表示x本身
- x取x的相反数
x % y模运算，求x除y的余数。10 % 3 结果为1
x ** y幂运算，求 xy。9 ** 0.5 结果为3.0
2.2 增强赋值操作符
增强赋值操作符及使用说明x += y与 x = x + y 等价
x -= y与 x = x - y 等价
x *= y与 x = x * y 等价
x /=y与 x = x / y 等价
x //= y与 x = x // y 等价
x %= y与 x = x % y 等价
x **= y与 x = x ** y 等价
三、数值运算函数( abs()、divmod()、pow()、round()、max()、min()、int()、float()、complex() )
数值运算函数及使用说明abs(x)绝对值函数，求x的绝对值
divmod(x, y)商余函数，同时求 x // y 和 x % y 。divmod(10, 3) 结果为(3, 1)
pow(x, y[, z])幂余函数，求 (x ** y)%z 。z省略则代表求 xy
round(x[, d])四舍五入函数，对 x 四舍五入，d 是保留的小数位数。d 省略则代表对 x 四舍五入取整
max(x1, x2, x3, …, xn)最大值函数，求 x1, x2, x3, …, xn 中的最大值，n 不限
min(x1, x2, x3, …, xn)最小值函数，求 x1, x2, x3, …, xn 中的最小值，n 不限
int(x)取整函数，直接舍弃x的小数部分。int(123.123) 结果为123，int(“123”) 结果为123
float(x)取浮点函数，为x添加小数部分。float(123) 结果为123.0，float(“1.23”) 结果为1.23
complex(x)取复数函数，为x添加虚数部分。complex(123) 结果为 123 + 0j
四、天天向上实例
1.1 实例1
# 每天进步1%。
dayup = pow(1.001, 365)
# 每天退步1%。
daydown = pow(0.999, 365)
print("向上：{:.2f}，向下：{:.2f}".format(dayup, daydown))
1.1 实例2
dayfactor = 0.001# 定义每天进步的参数
# 每天进步1%。
dayup = pow(1 + dayfactor, 365)
# 每天退步1%。
daydown = pow(1 - dayfactor, 365)
print("向上：{:.2f}，向下：{:.2f}".format(dayup, daydown))
1.1 实例3
'''''''''''''''''''''''''''''''
一年365天中，工作日每天进步1%
周六日每天退步1%
'''''''''''''''''''''''''''''''
dayup = 1.0# 定义初始进步
dayfactor = 0.01# 定义每天进步的参数
# 进行365天循环，i = 0, 1, 2, ..., 364
for i in range(365):
if i % 7 in [6, 0]:# 周六日退步1%
dayup *= (1 - dayfactor)
else:# 工作日进步1%
dayup *= (1 + dayfactor)
print("工作日的力量：{:.2f}".format(dayup))
1.1 实例4
小明：一年365天，每天进步1%，不停歇
玲玲：一年365天，每周工作5天休息2天，休息日每日退步1%，那玲玲在工作日平均每天要进步多少，最后才能和小明的进步相当呢？
流程图如下：
Created with Raphaël 2.2.0
开始
计算小明365天进步结果M
假设玲玲工作日平均每天进步1%
计算玲玲365天进步结果N
N≥M吗？
输出x
结束
x增加千分之一
yes
no
# 计算小明365天的进步量
Ming_dayup = pow(1.01, 365)
''' @brief 用于计算玲玲365天的进步量
'' @param df: 玲玲工作日平均每天进步的参数
'' @retval 玲玲365天的进步量
'''
def Ling_dayup(df):
dayup = 1# 定义玲玲的初始进步
# 进行365天循环，i = 0, 1, 2, ..., 364
for i in range(365):
if i % 7 in [6, 0]:# 玲玲一周内2天退步1%
dayup *= (1 - 0.01)
else:# 玲玲一周内5天进步df
dayup *= (1 + df)
return dayup# 函数返回玲玲365天的进步量
'''''''''''' 主程序 ''''''''''''
Ling_dayfactor = 0.01# 假设玲玲工作日平均每天进步1%
while Ling_dayup(Ling_dayfactor) < Ming_dayup:# while循环判断，直到玲玲最后的进步量不小于小明的进步的时候，结束循环
Ling_dayfactor += 0.001
print("玲玲工作日每天应平均进步{:.3f}".format(Ling_dayfactor))
