之——从时序中获取信息
目录
之——从时序中获取信息
杂谈
正文
1.建模
2.方案A-马尔科夫假设
3.方案B-潜变量模型
4.简单实现
杂谈
很多连续的数据都是有前后的时间相关性的,并不是每一个单独的数据是随机出现的。在时序中会蕴含一些空间结构的变化信息、先验因素、趋势与常理。
而且序列数据在日常生活中是相当多的。
正文
1.建模
样本都是相互不独立的,存在一定的联合概率。

那么所有样本按照当前形式出现的概率就是如下:

也就是之前的会影响之后的。当然反过来写也是可以的,满足最上面的反序列。
而最后的核心就是我希望给定之前的能得到新的概率,也就是:

对此建模得到:
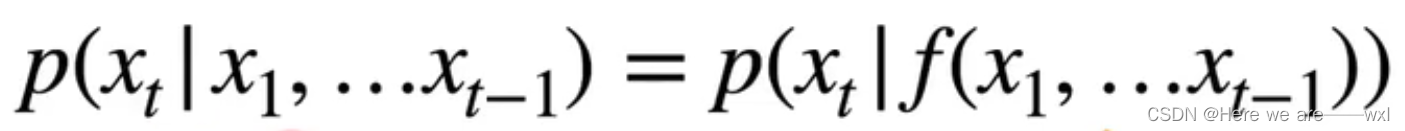
f就是要训练和学习的模型,被称为自回归模型,也即用模型预测下一个模型。
分解为两个任务,f的学习,p的产生。
2.方案A-马尔科夫假设
假设当前数据只跟τ个过去数据点相关。把往回看的视野规定一个长度,一个固定的视野长度。

这样子就是给一个定长向量要回归预测一个标量,那么就直接就是一个感知机的拟合就行。
3.方案B-潜变量模型
引入潜变量来表示过去信息。
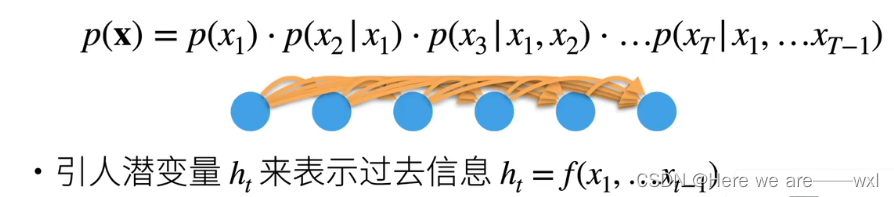
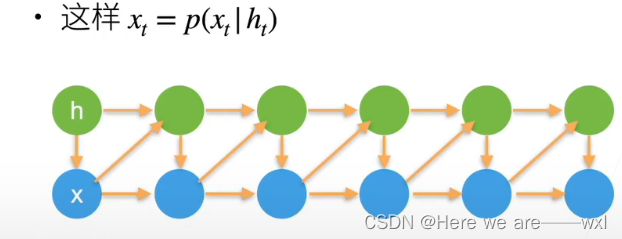
不断地更新潜在变量和新的变量。
4.简单实现
通过对一个加噪音的正弦函数进行一个数据配对来用马尔科夫进行拟合,实际上就是一个线性回归。
配对好然后进行训练:

细节见教材。这是一个极其简单的操作,真正比较有难度的是根据新生成的继续预测后面的数据,直接进行迭代是没戏的,每一次往后迭代的误差会不断累积,希望预测得越多,偏离会越离谱:




)

、getchar() 、putchar()、之间的关系)






)
使用方法介绍)





)