众所周知,逻辑回归常用于解决二分类任务,但是在工作/学习/项目中,我们也经常要解决多分类问题。本文总结了 3 种逻辑回归解决多分类的方法,并分析了他们的优缺点。
一、One-Vs-Rest
假设我们要解决一个分类问题,该分类问题有三个类别,分别用▲,■ 和 × 表示,每个实例(Entity)有两个属性(Attribute),如果把属性 1 作为 X 轴,属性 2 作为 Y 轴,训练集(Training Dataset)的分布可以表示为下图:
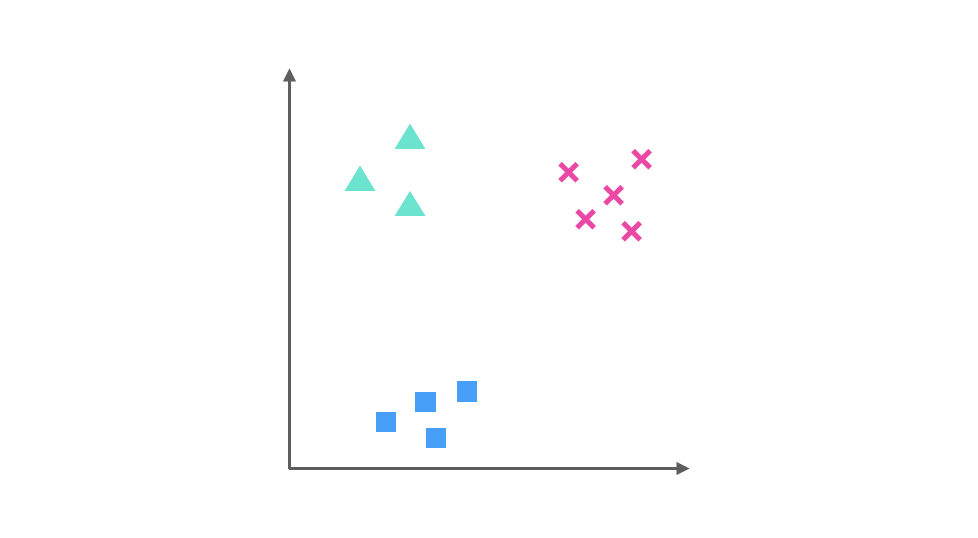
One-Vs-Rest 的思想是把一个多分类的问题变成多个二分类的问题。转变的思路是选择其中一个类别为正类(Positive),使其他所有类别为负类(Negative)。
比如第一步,我们将 ▲ 所代表的实例全部视为正类,其他实例全部视为负类,得到的分类器:
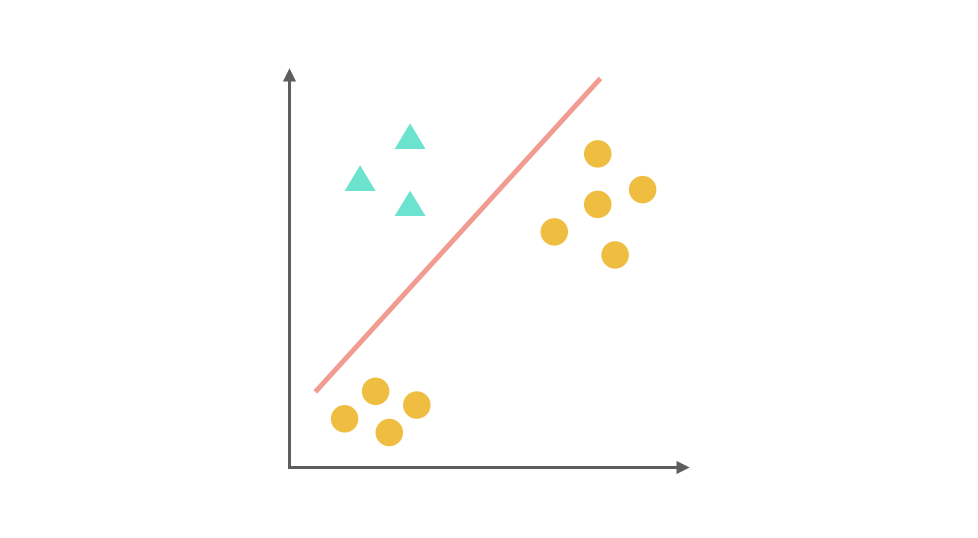
同理第二步,我们把 x 视为正类,其他视为负类,可以得到第二个分类器:
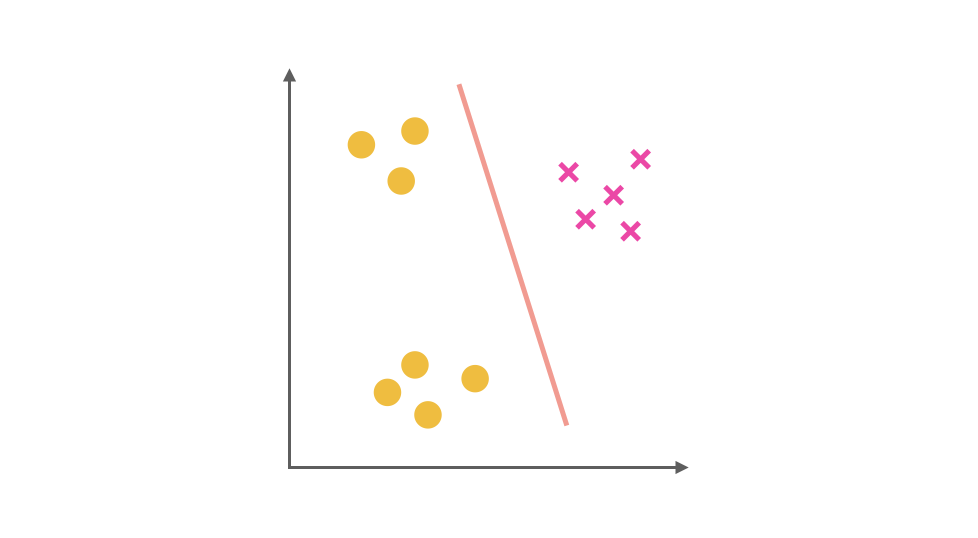
最后第三步,第三个分类器是把 ■ 视为正类,其余视为负类:
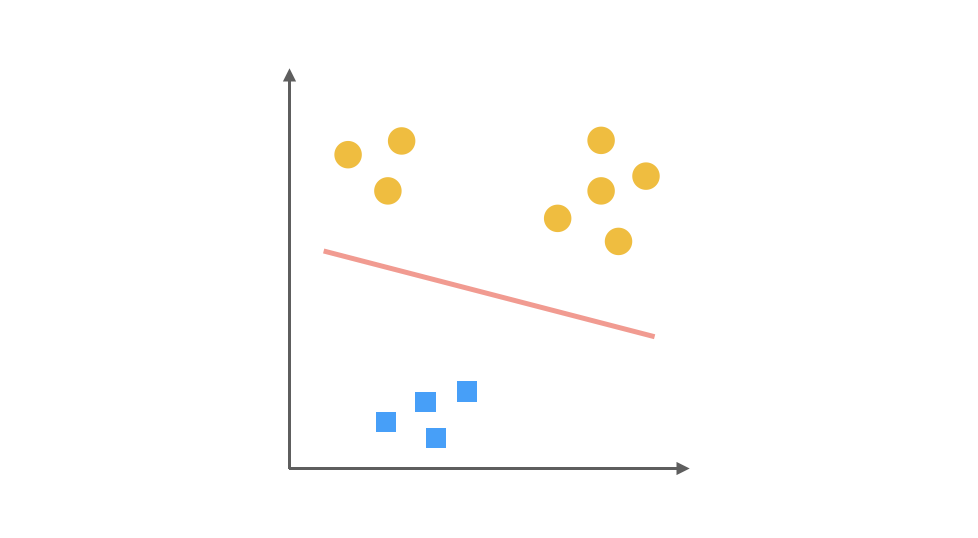
对于一个三分类问题,我们最终得到 3 个二元分类器。在预测阶段,每个分类器可以根据测试样本,得到当前正类的概率,即 P(y = i | x; θ),i = 1, 2, 3。选择计算概率结果最高的分类器,其正类就可以作为预测结果。
【优点】普适性比较广,可以应用于能输出值或者概率的分类器,同时效率相对较好,有多少个类别就训练多少个分类器。
【缺点】很容易造成训练集样本数量的不平衡(Unbalance),尤其在类别较多的情况下,经常容易出现正类样本的数量远远不及负类样本的数量,这样就会造成分类器的偏向性。
二、One-VS-One
相比于 One-Vs-Rest 由于样本数量可能的偏向性带来的不稳定性,One-Vs-One 是一种相对稳健的扩展方法。对于同样的三分类问题,我们让不同类别的数据两两组合训练分类器,可以得到 3 个二元分类器。
它们分别是 ▲ 与 x 训练得出的分类器:
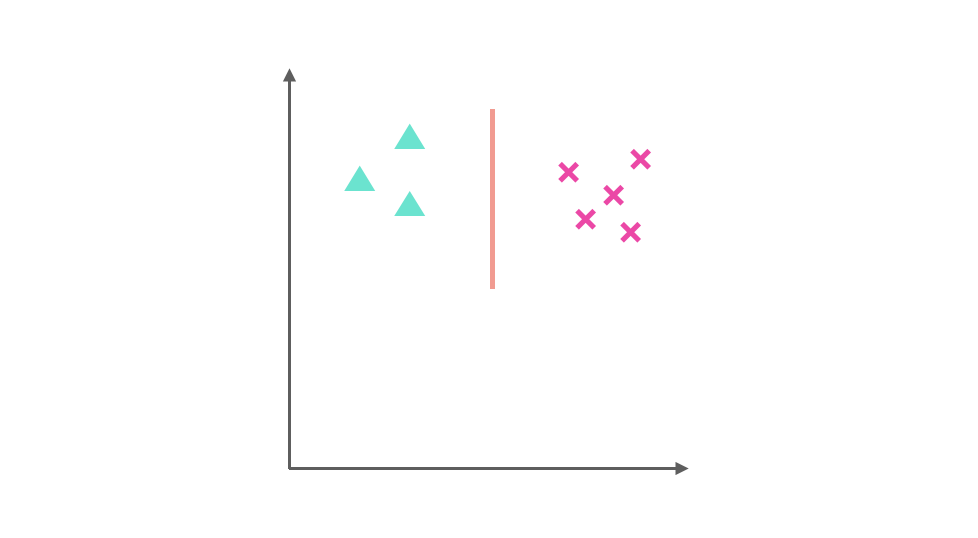
▲ 与 ■ 训练的出的分类器:
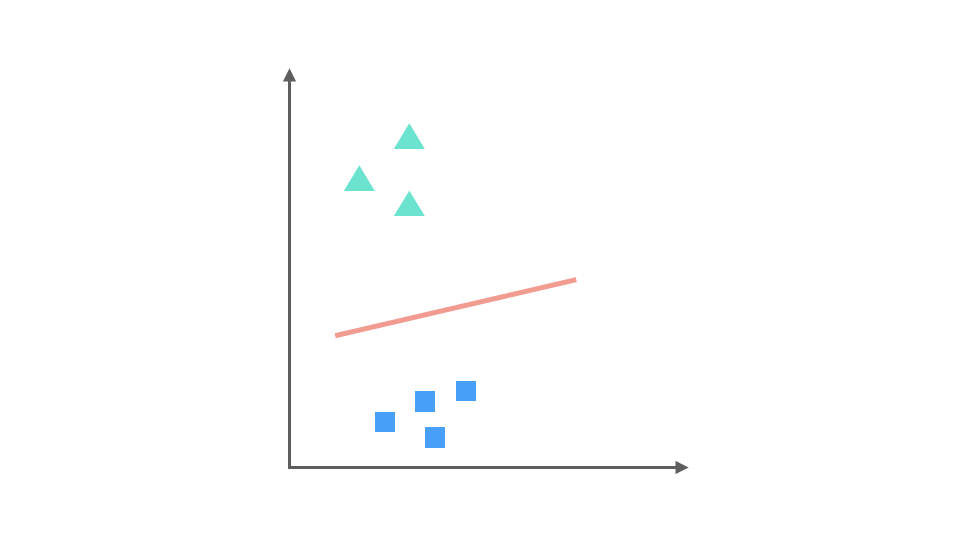
以及 ■ 与 x 训练得出的分类器:
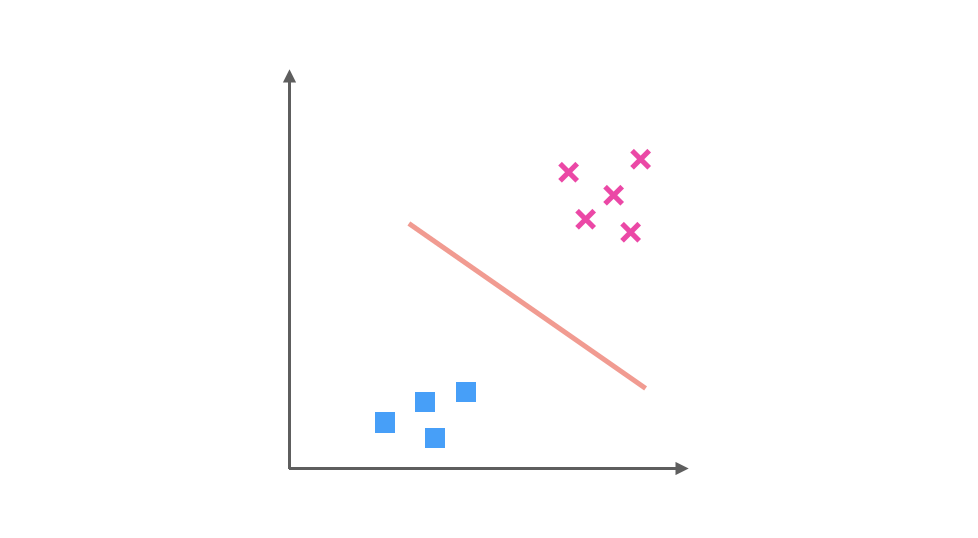
假如我们要预测的一个数据在图中红色圆圈的位置,那么第一个分类器会认为它是 x,第二个分类器会认为它偏向▲,第三个分类器会认为它是 x,经过三个分类器的投票之后,可以预测红色圆圈所代表的数据的类别为 x。
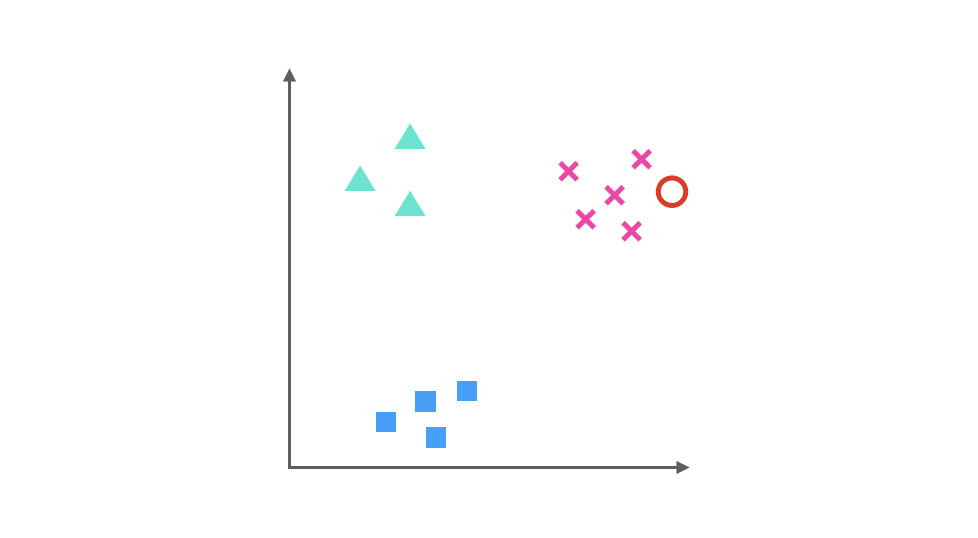
【优点】在一定程度上规避了数据集 unbalance 的情况,性能相对稳定,并且需要训练的模型数虽然增多,但是每次训练时训练集的数量都降低很多,其训练效率会提高。
【缺点】训练出更多的 Classifier,会影响预测时间。如果有 k 个不同的类别,对于 One-Vs-All 来说,一共只需要训练 k 个分类器,而 One-Vs-One 则需训练 C(k, 2) 个分类器,只是因为在本例种,k = 3 时恰好两个值相等,一旦 k 值增多,One-Vs-One 需要训练的分类器数量会大大增多。
三、Softmax 函数
该模型将逻辑回归推广到分类问题,其中类标签 y 可以采用两个以上的可能值。这对于诸如MNIST数字分类之类的问题将是有用的,其中目标是区分10个不同的数字。
在softmax回归中,我们对多类分类感兴趣(而不是仅对二元分类),所以y可以取k个不同的取值。因此,在我们的训练集
给定测试输入 x ,我们希望模型估计每个类别的概率。因此,模型将输出k维向量(其元素总和为1),给出 k 个类别的估计概率。具体地说,我们的假设
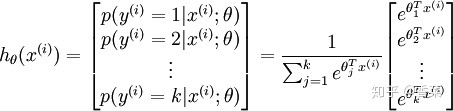
其中,
为方便起见,用向量法来表示模型的所有参数。当实现 softmax 回归时,将θ表示为通过堆叠
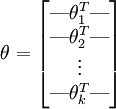
损失函数:
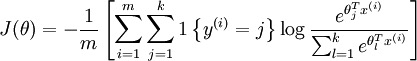
求导后,可得
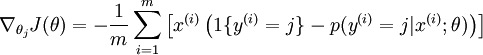
更新参数:
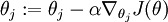
【注】 One-vs-Rest V.S. Softmax
假设正在处理音乐分类应用程序,并且正在尝试识别 k 种类型的音乐。您应该使用softmax分类器,还是使用逻辑回归构建k个单独的二元分类器呢?这取决于这四个类是否相互排斥。如果类别之间是互斥的,softmax 会比较合适,如果类别之间不是互斥的,用 OvR 比较合适。
例如,如果四个类是经典,乡村,摇滚和爵士乐,每个训练样例都标有这四个类别标签中的一个,那么您应该构建一个 k = 4 的 softmax 分类器,因为这些标签都是互斥的。但是,如果类别是舞蹈,配乐,流行音乐,那这些并不相互排斥,因为可以有一段来自音轨的流行音乐,另外还有人声。在这种情况下,构建 4 个二元逻辑回归分类器更合适。这样,对于每个新的音乐作品,算法可以单独决定它是否属于四个类别中的每一个。
总结,如果类别之间是互斥的,那么用 softmax 会比较合适,如果类别之间不是互斥的,用 OvR 比较合适。
参考:
[1]
力扣(LeetCode):3 种方法实现逻辑回归多分类zhuanlan.zhihu.com
[2]
飞鱼Talk:逻辑回归 - 4 逻辑回归与多分类zhuanlan.zhihu.com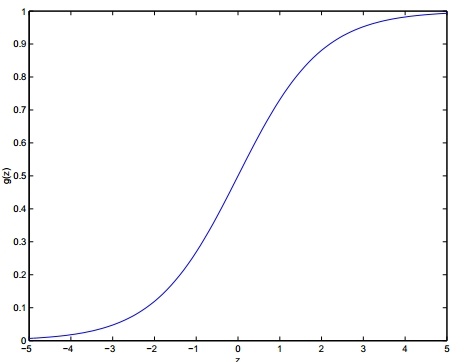







而官方提示必须是1.7.10及以后版本...)



)







