拒绝摆烂！C语言练习打卡第六天

🔥博客主页：小王又困了

📚系列专栏：每日一练

🌟人之为学，不日近则日退

❤️感谢大家点赞👍收藏⭐评论✍️

一、选择题

📝1.第一题

📝2.第二题

📝3.第三题

📝4.第四题

二、编程题

📝1.第一题

📝2.第二题

🗒️前言：

在前面我们学习完C语言的所以知识，当然练习巩固也不能落下。俗话说：“无财之谓贫，学而不能行之谓病。”可见实践对我们学习的重要。接下来就让小王带着大家进行练习，巩固我们C语言的学习。

一、选择题

📝1.第一题

若运行以下程序时，从键盘输入ADescriptor<回车> ，则下面程序的运行结果是（）

int main()
{char c;int v0 = 0, v1 = 0, v2 = 0;do{switch (c = getchar()){case'a':case'A':case'e':case'E':case'i':case'I':case'o':case'O':case'u':case'U':v1 += 1；default:v0 += 1; v2 += 1;}} while (c != '\n');printf("v0=%d,v1=%d,v2=%d\n", v0, v1, v2);return 0;
}

💡解题思路：

我们通过观察代码发现，这个程序读取字符，在switch语句中进行计算，当读到 ‘\0’ 时停止。判断是否是元音字母进行不同的计算，但是在本题switch语句中没有break，执行完case语句还会继续执行default语句。输入ADescriptor这串字符中有4个元音字母，所以case语句和default语句都执行，v0=v1=v2=4；其他7个字符只执行default语句，所以v1=4,v0=v2=11。但是这里要注意，本题使用的是do…while循环，先执行在判断，所以输入‘\0’也要执行语句，最后结果为v1=4,v0=v2=12。

📝2.第二题

下面代码 *pa 的值是（）

    float a[3] = { 1.5,2.5,3.5 };float* pa = a;*(pa++) *= 3;

💡解题思路：

a 是数组名，数组名是首元素地址，pa中存放的就是数组名是首元素地址。*(pa++) *= 3 这里是后置++，要先使用，再++。*pa 就是数组的首元素1.5，1.5*=3的结果为4.5，这时数组首元素的值被修改为4.5，这里我们不要忘记++，pa++就指向了2.5所在的位置，对pa解引用结果就是2.5。

📝3.第三题

若给定条件表达式 (M)?(a++):(a--) ，则下面表达式哪个 M 等价（）

A: 和(M==0)等价 B: 和(M==1)等价 C: 和(M!=0)等价 D: 和(M!=1)等价

💡解题思路：

我们观察题目，代码的意思是：M为真，执行a++；M为假，执行a--。当M非0时为真，M为0时为假。

选项A: M==0 的意思是，M为0时，表达式为真；M非0时，表达式为假，与题中M不等价。

选项B: M==1 的意思是，M为1时，表达式为真，但题意是M非0时为真，不等价。

选项C: M!=0 的意思是， M不等于0时为真，也就是非0；M为0，表达式为假，与M等价。

选项D: M!=1 的意思是， M不等于1时为真，但题意是M非0时为真，不等价。

📝4.第四题

test.c 文件中包括如下语句，文件中定义的四个变量中，是指针类型的变量为【多选】（）


define INT_PTR int*
typedef int* int_ptr;
INT_PTR a, b;
int_ptr c, d;

💡解题思路：

根据宏定义的理解，我们直接将INT_PTR给替换成int*,则为int*a，b;故可以判断出，a为指针变量，b不是，而typedef int* int_ptr相当于是给int*取了个叫int_ptr的类型，是一个将int和*联合在一起的整体，故c，d为指针变量

二、编程题

📝1.第一题

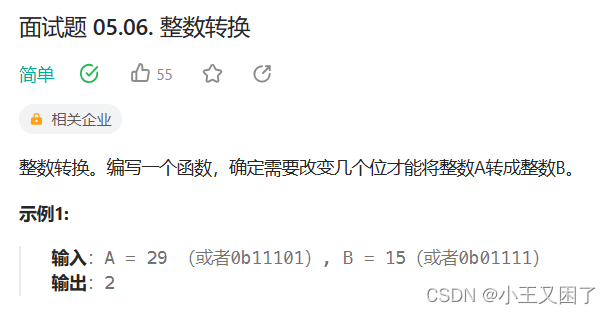
💡解题思路：

我们将A和B进行异或操作，异或的作用是对应的二进制位相同位0，相异为1。异或后我们只需要统计二进制中1个数，就可以知道A转成B要改变几位。

统计个数时，我们通过 num>>i&1==1 判断，条件成立计数器就加1。

& - 对应的二进制位有0，则为0；都为1，则为1
^ - 对应的二进制位相同位0，相异为1
int convertInteger(int A, int B)
{int num=A^B;int count=0;for(int i=0;i<32;i++){if(num>>i&1==1){count++;}}return count;
}

📝2.第二题

💡解题思路：

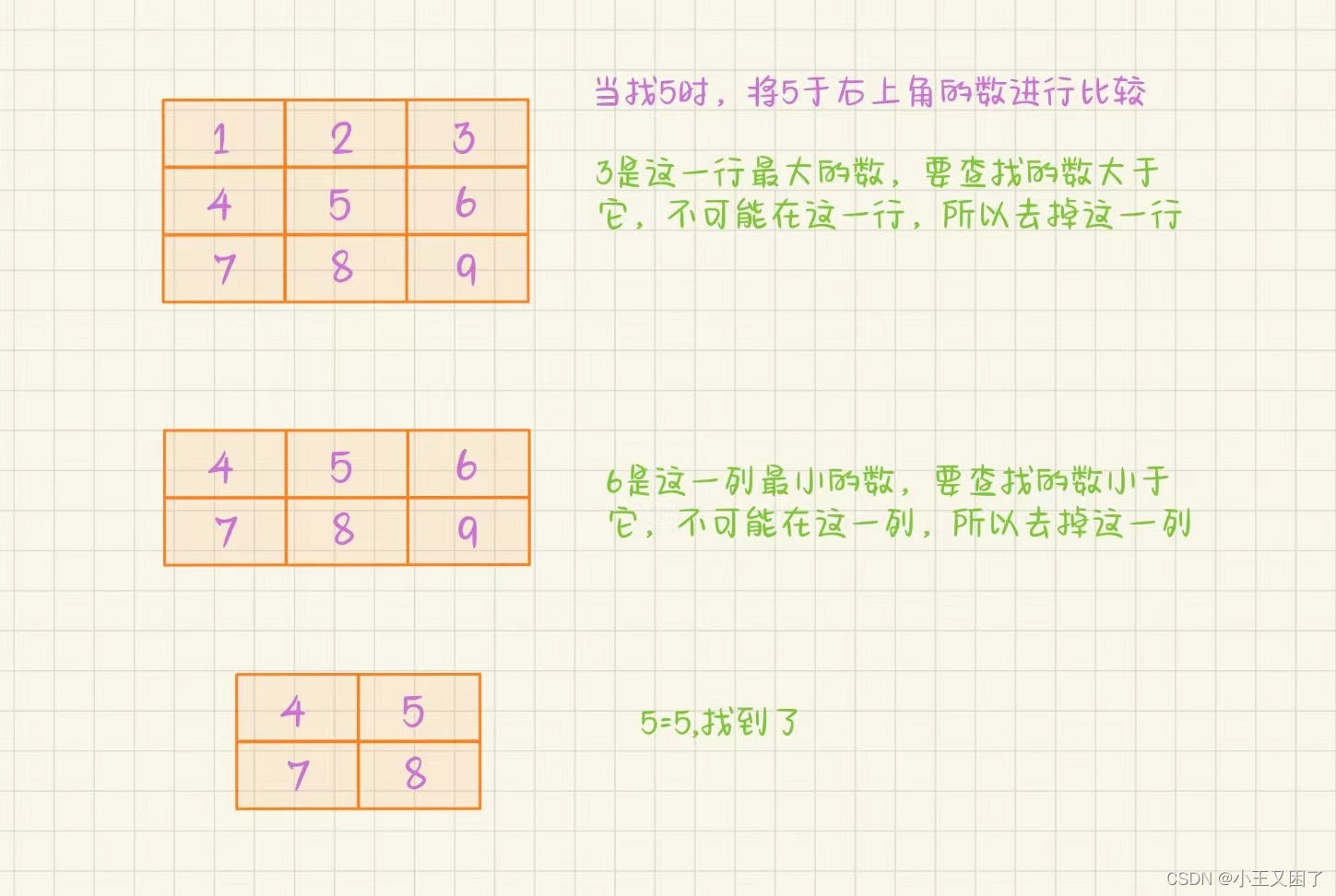
我们通过观察可以发现，杨氏矩阵的右上角的元素是有特点的，右上角的元素是一行中最大的，一列中最小的。我们从右上角开始查找，当右上角的元素比我们要查找的元素小，我们就可以去掉右上角元素所在的这一行；右上角的元素比我们要查找的元素大，我们就可以去掉右上角元素所在的这一列。然后继续找右上角的元素和要查找的值比较。这样每一次去掉一行或一列，小路远高于遍历数组元素。
int main()
{int k = 0;scanf("%d", &k);int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };int flag = 0;//右上角的元素int x = 0;int y = 2;while (x <= 2 && y >= 0){//去掉一行if (arr[x][y] < k){x++;}//去掉一列else if (arr[x][y] > k){y--;}else{printf("找到了,下标为%d %d\n", x, y);flag = 1;break;}}if (flag == 0){printf("找不到\n");}return 0;
}