k-近邻算法概述

k近邻（k-nearest neighbor, k-NN）算法由 Cover 和 Hart 于1968年提出，是一种简单的分类方法。通俗来说，就是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的 k 个实例，这 k 个实例的多数属于某个类，就把该输入实例分类到这个类中（类似于投票时少数服从多数的思想）。接下来读者来看下引自维基百科上的一幅图：

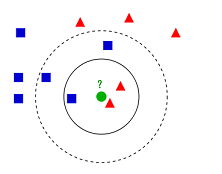
图1：数据

如上图 1 所示，有两类不同的样本数据，分别用蓝色的小正方形和红色的小三角形表示，而图正中间的那个绿色的圆所示的数据则是待分类的数据，那它的类别是什么？下面根据 k 近邻的思想来给绿色圆点进行分类。

如果 k=3，绿色圆点的最邻近的 3 个点是 2 个红色小三角形和 1 个蓝色小正方形，根据少数服从多数的思想，判定绿色的这个待分类点属于红色的三角形一类。如果 k=5，绿色圆点最邻近的 5 个邻居是 2 个红色三角形和 3 个蓝色的正方形，根据少数服从多数的思想，判定绿色的这个待分类点属于蓝色的正方形一类。

上面的例子形象展示了 k 近邻的算法思想，可以看出 k 近邻的算法思想非常简单。

k-近邻算法细节

k值的选取

假设有训练数据和待分类点如下图 2，图中有两类，一个是黑色的圆点，一个是蓝色的长方形，待分类点是红色的五边形。根据 k 近邻算法步骤来决定待分类点应该归为哪一类。读者能够看出来五边形离黑色的圆点最近，k 为1，因此最终判定待分类点是黑色的圆点。假设 k=1，那么测试样本的分类结果只受距离最近的一个样本影响，这种情况下模型很容易学习到噪声，出现过拟合。

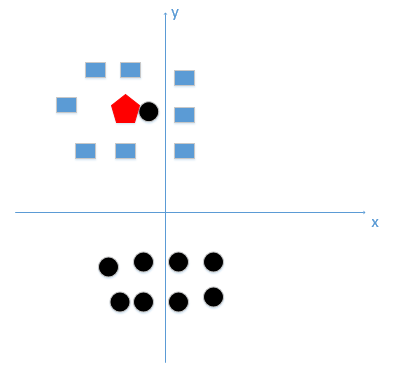
图2：训练数据

明显这样分类是错误的，此时距离五边形最近的黑色圆点是一个噪声，如果 k 太小，分类结果受距离最近的一些样本影响，这种情况下模型很容易学习到噪声，出现过拟合。

如果k大一点，k 等于8，把长方形都包括进来，很容易得到正确的分类应该是蓝色的长方形！如下图：

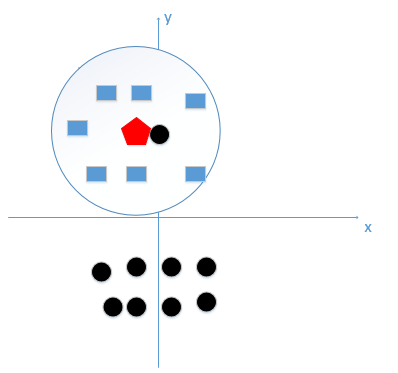
图3：k=8

如果K与训练样本的总数相等，那会出现什么样的分类结果呢？

如果 k=N（N为训练样本的个数），那么无论输入实例是什么，都将简单地预测它属于在训练实例中最多的类。这相当于没有训练模型！直接拿训练数据统计了一下各个数据的类别，找最大的而已！如下图所示：

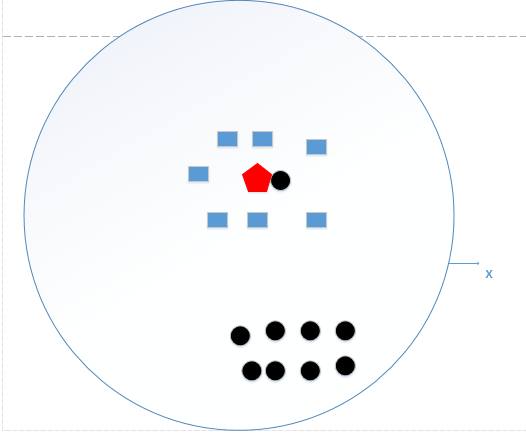
图3：k=N

为了避免出现以上两种极端情况，实践中我们会用到交叉验证，即从 k=1 开始，使用验证集去估计分类器的错误率，然后将 k 依次加1，每次计算分类器的整体错误率，不断重复这个过程，最后就能得到错误率最小的 k 值，这就是我们要找的合适的 k 值。需要注意的是，一般 k 的取值不超过20，并且要尽量取奇数，以避免在最终分类结果中出现样本数相同的两个类别。

分类器的决策

在上面几个例子中，判断待决策样本属于哪一类时，都是根据少数服从多数的思想。为什么根据这种思想做分类决策，背后的原理是什么呢？

假设分类的损失函数为0-1损失函数，分类函数为

k-means与k-NN的区别对比

k-means与k-NN是经常容易被混淆的两个算法，即使是做了多年机器学习的老江湖，也可能嘴瓢或者忘记两个算法的区分。

两种算法之间的根本区别是：

k-means是无监督学习，k-NN是监督学习；

k-means解决聚类问题，k-NN解决分类或回归问题。

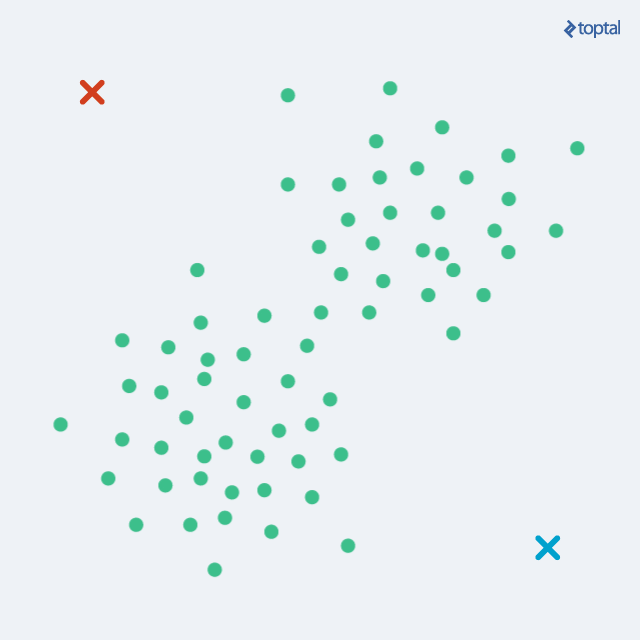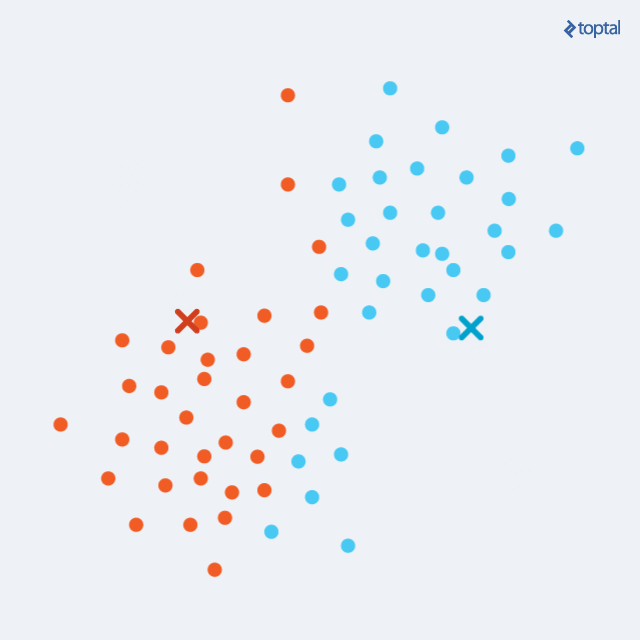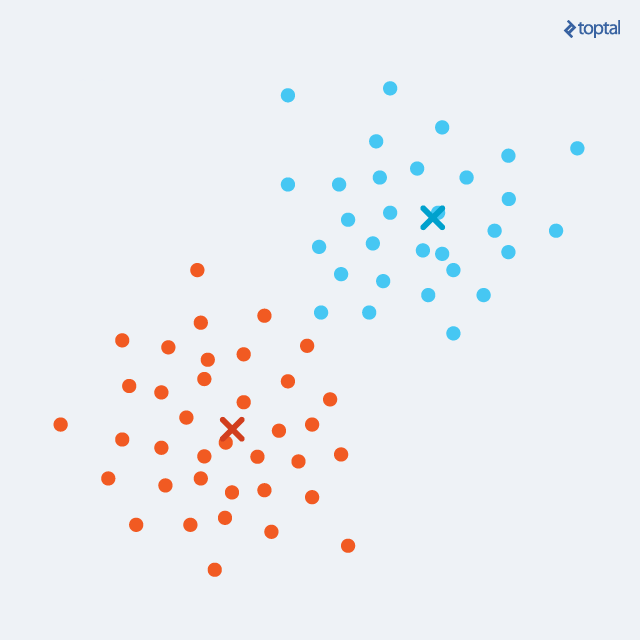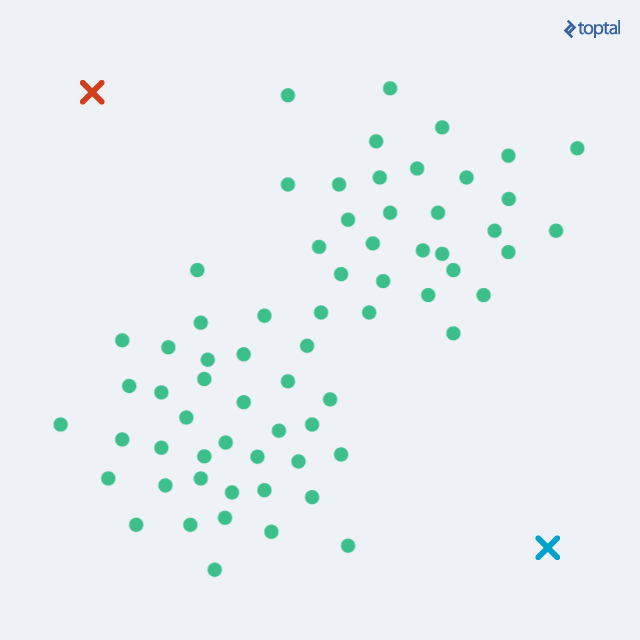
k-means算法把一个数据集分割成簇，使得形成的簇是同构的，每个簇里的点相互靠近

k-NN算法尝试基于其k个（可以是任何数目）周围邻居来对未标记的实例进行分类。

k-means算法的训练过程需要反复的迭代操作（寻找新的质心），但是k-NN不需要。

k-means中的k代表的是簇中心

k-NN的k代表的是选择与测试样本距离最近的前k个训练样本数。

	k-means	k-NN
学习范式	无监督学习算法	监督学习算法
提出时间	1967年	1968年
适用问题	解决聚类问题	解决分类或回归问题
核心思想	物以类聚，人以群分	近朱者赤，近墨者黑
算法原理	k-means是基于中心的聚类方法，通过迭代，将样本分到k个类中，使得每个样本与其所属类的中心或均值最近；得到k个类别，构成对空间的划分。	k-NN算法简单、直观，给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最近邻的k个实例，这k个实例的多数属于某个类，就把该输入实例分为这个类。
算法流程	k-means聚类的算法是一个迭代过程，每次迭代包括两个步骤。首先选择k个类的中心，将样本逐个指派到与其最近的中心的类中，得到一个聚类结果；然后更新每个类的样本的均值，作为类的新的中心；重复上述步骤，直到收敛为止。	(1)当有新的测试样本出现时，计算其到训练集中每个数据点的距离；（距离度量） (2)根据距离选择与测试样本距离最小的前k个训练样本；（k值选择） (3)基于这k个训练样本的类别来划分新样本的类别，通常选择这k个训练样本中出现次数最多的标签作为新样本的类别。（决策规则）
算法图示
k的意义	k是类的数目	k是用来计算的相邻数据数
k的选择	k是类的数目，是人为设定的数字。可以尝试不同的k值聚类，检验各自得到聚类结果的质量，推测最优的k值。聚类结果的质量可以用类的平均直径来衡量。一般地，类别数变小时，平均直径会增加；类别数变大超过某个值以后，平均直径会不变；而这个值正式最优的k值。实验时，可以采用二分查找，快速找到最优的k值。	k值的选择会对k-NN的结果产生重大影响。 ·如果选择较小的k值，就相当于用较小的邻域中的训练实例进行预测，“学习”的近似误差（approximation error）会减小，只有与输入实例较近的（相似的）训练实例才会对预测结果起作用。但缺点是“学习”的估计误差（estimation error）会增大，预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声，预测就会出错。换句话说，k值的减小就意味着整体模型变得复杂，容易发生过拟合。 ·如果选择较大的k值，就相当于用较大邻域中的训练实例进行预测。其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时与输入实例较远的（不相似的）训练实例也会对预测起作用，使预测发生错误。k值的增大就意味着整体的模型变得简单。 ·如果k=n，那么无论输入实例是什么，都将简单地预测它属于在训练实例中最多的类。这时，模型过于简单，完全忽略训练实例中的大量有用信息，是不可取的。 ·在应用中，k值一般取一个比较小的数值。通常采用交叉验证法来选取最优的k值。
k与结果	k值确定后每次结果可能不同，从 n 个数据对象任意选择 k 个对象作为初始聚类中心，随机性对结果影响较大。	k-NN算法中，当训练集、距离度量（如欧氏距离）、k值和决策规则（如多数表决）确定后，对于任何一个新输入的实例，它所属的类唯一确定。
复杂度	时间复杂度：O(nkt)，n为训练实例数，k为聚类数，t为迭代次数。	线性扫描时间复杂度：O(n) kd树方法时间复杂度：O(logn)
算法特点	是基于划分的聚类方法；类别数k事先指定；以欧氏距离平方表示样本之间的距离，以中心或样本的均值表示类别；以样本和其所属类的中心之间的距离的总和为最优化的目标函数；得到的类别是平坦的、非层次化的；算法是迭代算法，不能保证得到全局最优。	k-NN算法没有显式的学习过程；实现k-NN时，主要考虑问题是如何对训练数据进行快速k近邻搜索。
算法优点	1、解决聚类问题的经典算法，简单、快速； 2、当处理大数据集时，算法保持可伸缩性和高效率； 3、当簇近似为高斯分布时，效果较好； 4、时间复杂度近于线性，适合挖掘大规模数据集。	1、对输入数据无假定，如不会假设输入数据是服从正太分布； 2、k-NN可以处理分类问题，同时天然可以处理多分类问题，比如鸢尾花的分类； 3、简单，易懂，同时也很强大，对于手写数字的识别，鸢尾花这一类问题来说，准确率很高； 4、k-NN还可以处理回归问题，也就是预测； 5、对异常值不敏感； 6、可以用于数值型数据，也可以用于离散型数据。
算法缺点	1、类别数k需要事先指定； 2、对初值敏感，即对于不同的初值，可能会导致不同结果； 3、不适合非凸形状的簇或者大小差别很大的簇； 4、对噪声和孤立点敏感； 5、属于启发式算法，不能保证得到全局最优。	1、计算复杂度高，线性扫描方法需要计算输入实例与每一个训练实例的距离，当训练集很大时，计算非常耗时；可以通过kd树等方法改进； 2、严重依赖训练样本集，对训练数据的容错性差，如果训练数据集中，有一两个数据是错误的，刚刚好又在需要分类的数值的旁边，就会直接导致预测的数据的不准确； 3、距离度量方法以及k值的选取都有比较大的影响，k值选择不当则分类精度不能保证。
相似点	都包含这样的过程，给定一个点，在数据集中找离它最近的点，即二者都用到了NN（Nearest Neighbor）算法，一般用kd树来实现NN。