一. 前言

又GET了一项技能。在做聚类算法的时候，由于要评估所提出的聚类算法的好坏，于是需要与一些已知的算法对比，或者用一些人工标注的标签来比较，于是用到了聚类结果的评估指标。我了解了以下几项。

TP:是指被聚在一类的两个量被正确的分类了(即在标准标注里属于一类的两个对象被聚在一类)

TN:是指不应该被聚在一类的两个对象被正确地分开了(即在标准标注里不是一类的两个对象在待测结果也没聚在一类)

FP：指不应该放在一类的对象被错误的放在了一类。(即在标准标注里不是一类，但在待测结果里聚在一类)

FN：指不应该分开的对象被错误的分开了。(即在标准标注里是一类，但在待测结果里没聚在一类)

P = TP + FP

N = TN + FN

1.准确率、识别率：(rank Index)  RI

accuracy = (TP + TN)/(P + N)

2.错误率、误分类率

error rate = (FP + FN)/(P + N)

3.敏感度

sensitivity = TP / P

4.特效性

specificity = TN / N

5.精度

precision = TP  /   (TP + FP)

6.召回率

recall  =  TP  /   (TP  + FN)

7.RI  其实就是  1  的 accuracy

8.F度量

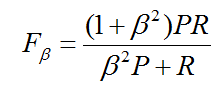
P为precision

R为recall

9.NMI(normalized mutual information)

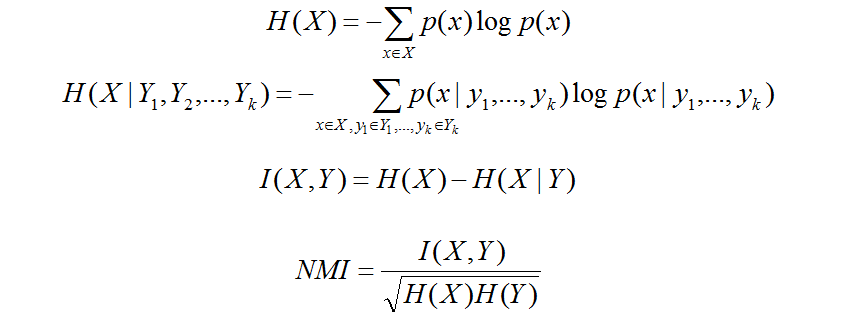
10 Jaccard

J = TP  / (TP + F)

二、JAVA实现(未优化)

其中很多重复代码，还没有优化。。。

package others;

import java.util.HashMap;

import java.util.HashSet;

import java.util.Iterator;

import java.util.Map;

import java.util.Map.Entry;

import java.util.Set;

import javax.rmi.CORBA.Util;

import org.graphstream.algorithm.measure.NormalizedMutualInformation;

/*function:常用的聚类评价指标有purity, precision, recall， RI 和 F-score,jaccard

* @param:

* @author:Wenbao Li

* @Data:2015-07-13

*/

public class ClusterEvaluation {

public static void main(String[] args){

int[] A = {1,3,3,3,3,3,3,2,1,0,2,0,2,0,2,1,1,0,1,1};

int[] B = {2,2,0,0,0,3,2,2,3,1,3,1,0,1,2,1,0,1,3,3};

double purity = Purity(A,B);

System.out.println("purity\t\t"+purity);

System.out.println("Pre\t\t"+Precision(A,B));

System.out.println("Recall\t\t"+Recall(A,B));

System.out.println("RI(Accuracy)\t\t"+RI(A,B));

System.out.println("Fvalue\t\t"+F_score(A,B));

System.out.println("NMI\t\t"+NMI(A,B));

}

/*

* 计算一个聚类结果的簇的个数，以及每一簇中的对象个数,

*/

public static Map> clusterDistri(int[] A){

Map> clusterD = new HashMap>();

int max = -1;

for(int i = 0;i< A.length;i++){

if(max < A[i]){

max = A[i];

}

}

for(int i = 0;i< A.length;i++){

int temp = A[i];

if(temp < max+1){

if(clusterD.containsKey(temp)){

Set set = clusterD.get(temp);

set.add(i+1);

clusterD.put(temp, set);

}else{

Set set = new HashSet();

set.add(i+1);

clusterD.put(temp, set);

}

}

}

return clusterD;

}

public static double ClusEvaluate(String method,int[] A,int[] B){

switch(method){

case "Purity":

return Purity(A,B);

case "Precision":

return Precision(A,B);

case "Recall":

return Recall(A,B);

case "RI":

return RI(A,B);

case "F_score":

return F_score(A,B);

case "NMI":

return NMI(A,B);

case "Jaccard":

return Jaccard(A,B);

default:

return -1.0;

}

}

public static int[] commNum(Map> A,Map> B){

int[] commonNo = new int[A.size()];

int com = 0;

Iterator>> itA = A.entrySet().iterator();

int i = 0;

while(itA.hasNext()){

Entry> entryA = itA.next();

Set setA = entryA.getValue();

Iterator>> itB = B.entrySet().iterator();

int maxComm = -1;

while(itB.hasNext()){

Entry> entryB = itB.next();

Set setB = entryB.getValue();

int lengthA = setA.size();

Set temp = new HashSet(setA);

temp.removeAll(setB);

int lengthCom = lengthA - temp.size();

if(maxComm < lengthCom){

maxComm = lengthCom;

}

}

commonNo[i] = maxComm;

com = com + maxComm;

i++;

}

return commonNo;

}

/*

* 所有簇分配正确的除以总的。其中B是对比的标准标签。

*/

public static double Purity(int[] A,int[] B){

double value;

Map> clusterA = clusterDistri(A);

Map> clusterB = clusterDistri(B);

int[] commonNo = commNum(clusterA,clusterB);

int com = 0;

for(int i = 0;i

com = com + commonNo[i];

}

value = com*1.0/A.length;

return value;

}

/*

* @param A,B

* @return 精度

*/

public static double Precision(int[] A,int[] B){

double value = 0.0;

Map> clusterA = clusterDistri(A);//得到聚类结果A的类分布

Map> clusterB = clusterDistri(B);//得到聚类B(标准)的类分布

int[] commonNo = commNum(clusterA,clusterB);//得到A中每个簇中聚类正确的数目。

int allP = 0;

int TP = 0;

int FP = 0;

int TN = 0;

int FN = 0;

Iterator>> itA = clusterA.entrySet().iterator();

int i = 0;

while(itA.hasNext()){

Entry> entryA = itA.next();

allP = allP + combination(entryA.getValue().size(),2);

TP = TP + combination(commonNo[i],2);

i++;

}

FP = allP - TP;

itA = clusterA.entrySet().iterator();

while(itA.hasNext()){

Entry> entryA = itA.next();

Iterator>> itA2 = clusterA.entrySet().iterator();

while(itA2.hasNext()){

Entry> entryA2 = itA2.next();

if(entryA != entryA2){

Set s1 = entryA.getValue();

Set s2 = entryA2.getValue();

for(Integer i1 :s1){

for(Integer i2:s2){

if(B[i1-1] != B[i2-1]){

TN++;

}else{

FN++;

}

}

}

}

}

}

double P = TP*1.0/(TP + FP);

return P;

}

/*

* @param A,B

* @return recal召回率

*/

public static double Recall(int[] A,int[] B){

double value = 0.0;

Map> clusterA = clusterDistri(A);//得到聚类结果A的类分布

Map> clusterB = clusterDistri(B);//得到聚类B(标准)的类分布

int[] commonNo = commNum(clusterA,clusterB);//得到A中每个簇中聚类正确的数目。

int allP = 0;

int TP = 0;

int FP = 0;

int TN = 0;

int FN = 0;

Iterator>> itA = clusterA.entrySet().iterator();

int i = 0;

while(itA.hasNext()){

Entry> entryA = itA.next();

allP = allP + combination(entryA.getValue().size(),2);

TP = TP + combination(commonNo[i],2);

i++;

}

FP = allP - TP;

itA = clusterA.entrySet().iterator();

while(itA.hasNext()){

Entry> entryA = itA.next();

Iterator>> itA2 = clusterA.entrySet().iterator();

while(itA2.hasNext()){

Entry> entryA2 = itA2.next();

if(entryA != entryA2){

Set s1 = entryA.getValue();

Set s2 = entryA2.getValue();

for(Integer i1 :s1){

for(Integer i2:s2){

if(B[i1-1] != B[i2-1]){

TN++;

}else{

FN++;

}

}

}

}

}

}

double R = TP * 1.0/(TP + FN);

return R;

}

/*

* @param A,B

* @return RankIndex

*/

public static double RI(int[] A,int[] B){

double value = 0.0;

Map> clusterA = clusterDistri(A);//得到聚类结果A的类分布

Map> clusterB = clusterDistri(B);//得到聚类B(标准)的类分布

int[] commonNo = commNum(clusterA,clusterB);//得到A中每个簇中聚类正确的数目。

int P = 0;

int TP = 0;

int FP = 0;

int TN = 0;

int FN = 0;

Iterator>> itA = clusterA.entrySet().iterator();

int i = 0;

while(itA.hasNext()){

Entry> entryA = itA.next();

P = P + combination(entryA.getValue().size(),2);

TP = TP + combination(commonNo[i],2);

i++;

}

FP = P - TP;

itA = clusterA.entrySet().iterator();

while(itA.hasNext()){

Entry> entryA = itA.next();

Iterator>> itA2 = clusterA.entrySet().iterator();

while(itA2.hasNext()){

Entry> entryA2 = itA2.next();

if(entryA != entryA2){

Set s1 = entryA.getValue();

Set s2 = entryA2.getValue();

for(Integer i1 :s1){

for(Integer i2:s2){

if(B[i1-1] != B[i2-1]){

TN++;

}else{

FN++;

}

}

}

}

}

}

value = (TP + TN)*1.0/(TP + FP + FN + TN);

return value;

}

/*

* F值，是对精度和召回率的平衡，

* @param A:评估对象。B：评估标准；beta：均衡参数

* @return F值

*/

public static double F_score(int[] A,int[] B){

double beta = 1.0;

double value = 0.0;

Map> clusterA = clusterDistri(A);//得到聚类结果A的类分布

Map> clusterB = clusterDistri(B);//得到聚类B(标准)的类分布

int[] commonNo = commNum(clusterA,clusterB);//得到A中每个簇中聚类正确的数目。

int allP = 0;

int TP = 0;

int FP = 0;

int TN = 0;

int FN = 0;

Iterator>> itA = clusterA.entrySet().iterator();

int i = 0;

while(itA.hasNext()){

Entry> entryA = itA.next();

allP = allP + combination(entryA.getValue().size(),2);

TP = TP + combination(commonNo[i],2);

i++;

}

FP = allP - TP;

itA = clusterA.entrySet().iterator();

while(itA.hasNext()){

Entry> entryA = itA.next();

Iterator>> itA2 = clusterA.entrySet().iterator();

while(itA2.hasNext()){

Entry> entryA2 = itA2.next();

if(entryA != entryA2){

Set s1 = entryA.getValue();

Set s2 = entryA2.getValue();

for(Integer i1 :s1){

for(Integer i2:s2){

if(B[i1-1] != B[i2-1]){

TN++;

}else{

FN++;

}

}

}

}

}

}

double P = TP*1.0/(TP + FP);

double R = TP * 1.0/(TP + FN);

value = (beta*beta + 1)*P * R/(beta*beta*P + R);

return value;

}

public static double Jaccard(int[] A,int[] B){

double value = 0.0;

Map> clusterA = clusterDistri(A);//得到聚类结果A的类分布

Map> clusterB = clusterDistri(B);//得到聚类B(标准)的类分布

int[] commonNo = commNum(clusterA,clusterB);//得到A中每个簇中聚类正确的数目。

int allP = 0;

int TP = 0;

int FP = 0;

int TN = 0;

int FN = 0;

Iterator>> itA = clusterA.entrySet().iterator();

int i = 0;

while(itA.hasNext()){

Entry> entryA = itA.next();

allP = allP + combination(entryA.getValue().size(),2);

TP = TP + combination(commonNo[i],2);

i++;

}

FP = allP - TP;

itA = clusterA.entrySet().iterator();

while(itA.hasNext()){

Entry> entryA = itA.next();

Iterator>> itA2 = clusterA.entrySet().iterator();

while(itA2.hasNext()){

Entry> entryA2 = itA2.next();

if(entryA != entryA2){

Set s1 = entryA.getValue();

Set s2 = entryA2.getValue();

for(Integer i1 :s1){

for(Integer i2:s2){

if(B[i1-1] != B[i2-1]){

TN++;

}else{

FN++;

}

}

}

}

}

}

value = TP * 1.0 / (TP + FP + FN);

return value;

}

public static double NMI(int[] A,int[] B){

Map> clusterA = clusterDistri(A);//得到聚类结果A的类分布

Map> clusterB = clusterDistri(B);//得到聚类B(标准)的类分布

Iterator>> itA = clusterA.entrySet().iterator();

Iterator>> itB = clusterB.entrySet().iterator();

Set> partitionF = new HashSet>();

Set> partitionR = new HashSet>();

int nodeCount = B.length;

while(itA.hasNext()){

Entry> entryA = itA.next();

Set setA = entryA.getValue();

partitionF.add(setA);

setA = null;

entryA = null;

}

while(itB.hasNext()){

Entry> entryB = itB.next();

Set setB = entryB.getValue();

partitionR.add(setB);

setB = null;

entryB = null;

}

return computeNMI(partitionF,partitionR,nodeCount);

}

public static double computeNMI(Set> partitionF,

Set> partitionR,int nodeCount) {

int[][] XY = new int[partitionR.size()][partitionF.size()];

int[] X = new int[partitionR.size()];

int[] Y = new int[partitionF.size()];

int i = 0;

int j = 0;

for (Set com1 : partitionR) {

j = 0;

for (Set com2 : partitionF) {

XY[i][j] = intersect(com1, com2);//待测结果第i个簇和标准结果第j个簇的共有元素个数

X[i] += XY[i][j];//待测结果第i个簇与所有标准结果簇的公共元素个数(感觉就是第i个簇的元素个数)

Y[j] += XY[i][j];//标准结果簇第j个簇的元素个数()

j++;

}

i++;

}

int N = nodeCount;

double Ixy = 0;

double Ixy2 = 0;

for (i = 0; i < partitionR.size(); i++) {

for (j = 0; j < partitionF.size(); j++) {

if (XY[i][j] > 0) {

Ixy += ((double) XY[i][j] / N)

* (Math.log((double) XY[i][j] * N / (X[i] * Y[j])) / Math

.log(2.0));

//Ixy2 = (float) (Ixy2 + -2.0D * XY[i][j]

//* Math.log(XY[i][j] * N / X[i] * Y[j]));

}

}

}

//System.out.println(Ixy2);

//double denom = 0.0F;

//for (int ii = 0; ii < X.length; ++ii)

//denom = (double) (denom + X[ii] * Math.log(X[ii] / N));

//for (int jj = 0; jj < Y.length; ++jj) {

//denom = (double) (denom + Y[jj] * Math.log(Y[jj] / N));

//}

//

//System.out.println(denom);

//double M = (Ixy / denom);

//

//return M;

double Hx = 0;

double Hy = 0;

for (i = 0; i < partitionR.size(); i++) {

if (X[i] > 0)

Hx += h((double) X[i] / N);

}

for (j = 0; j < partitionF.size(); j++) {

if (Y[j] > 0)

Hy += h((double) Y[j] / N);

}

double InormXY = Ixy / Math.sqrt(Hx * Hy);

return InormXY;

}

private static double h(double p) {

return -p * (Math.log(p) / Math.log(2.0));

}

/*

* 两个集合的公共元素个数

*/

private static int intersect(Set com1, Set com2) {

int num = 0;

for (Integer v1 : com1) {

if (com2.contains(v1))

num++;

}

return num;

}

/*

* C(m,n)=m取n

*/

public static int combination(int m,int n){

int result = 1;

if(m < n){

return -1;

}

result = factorial(m)/(factorial(n)*factorial(m-n));

return result;

}

public static int factorial(int m){

if((m == 1) || (m == 0)){

return 1;

}else if(m < 0){

return -1;

}else{

return m*factorial(m-1);

}

}

}