一、麦克斯韦基于四元数观点导出散度与旋度
已知的最早的关于散度和旋度的描述都来自麦克斯韦1873年的《A Treatise on Electricity and Magnetism》(电磁通论)一书。因此,为了探明散度和旋度的物理意义,有必要回到那本1873年的专著来看。
麦克斯韦的观点(四元数观点)
麦克斯韦很大程度上继承了哈密顿的四元数观点。四元数论认为,四维空间中的一点可以通过通过
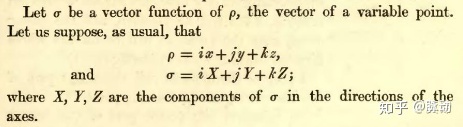
随后,麦克斯韦对
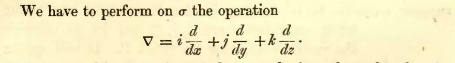
根据四元数的乘法规则,
可以得到所乘结果的标量部和向量部分别是
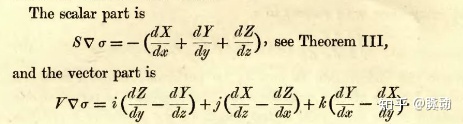
麦克斯韦发现,算子的标量部和向量部分别可以和两个定理对应起来。这两个定理就是位于其书中铺垫部分的第21节的定理三
通量指向一个闭合曲面内部的面积分,可以表示成在曲面内部所求散度的体积分
以及第24节的定理四
沿一条闭合曲线计算的一个线积分,可以用以该曲线为边的一个曲面上的面积分表示出来。
其实这两个定理就是高数中的高斯公式(将闭合曲面积分换成体积分)和斯托克斯公式(将环路线积分换成曲面积分)。
也就是说,麦克斯韦的思路是:通过数学计算证明高斯公式和斯托克斯公式 → 通过四元数计算得到
麦克斯韦认为,标量部的结果可以这么解释。假设
麦克斯韦建议把算子的标量部称为 convergence(散度)。早期教材也有称为敛度的。

至于算子的向量部,麦克斯韦认为,可以假设从该向量的方向来看。同样地,审视
麦克斯韦建议把算子的向量部称为 curl 或 version(旋度)。

参考:知乎解答 和 四元数的运算规则
二、现代电动力学里的物理意义
- 矢量场
的散度
设闭合曲面围着体积
,当
时,
对
通量与的
之比的极限称为
的散度,即
2. 矢量场
设闭合曲线围着面积
,当
时,
对
的环量与
之比的极限称为
的旋度沿着该面法线的分量,即
3. 标量场
设沿线元上,标量场
的数值改变
,
称为梯度沿着
方向上的分量,即
4. 由以上定义可得积分变换
于是在直角坐标系中利用微分算子
参考:《电动力学》
三、数学上的总结
矢量微分算子
在
- 梯度
函数
2. 散度
矢量
3. 旋度
矢量
4. 拉普拉斯算子
表示为
它作用于函数
它作用于矢量
5. 常用运算
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
参考:渔樵《数学物理方法》
四、 一些不同的解释
(1)通量是单位时间内通过的某个曲面的量;散度是通量强度。
环流量是单位时间内环绕的某个曲线的量;旋度是环流量强度。
(2)散度:单位体积的通量。旋度:单位面积的环量。梯度:单位长度的变量。
(3)散度是闭合曲面围成空间中的通量除以围成空间体积,然后令曲面无限小。
旋度是闭合曲线围成面积中的环流除以围成范围面积,然后令曲线无限小。(这个闭合曲线围成的面要选择环流最大的那个面,而旋度的方向就是这个最大面的法线方向)
(4)从物理的角度这样理解:
散度就是点电荷的电量密度,可以通过对电量密度的体积分求电通量,反之亦然;
旋度就是导线的电流密度,可以通过对电流密度面积分求围绕导线一圈的磁场强度的闭合环路积分,反之亦然。同时旋度方向可理解为导线的电流方向。
(5)看了回答,感觉都没有回答到物理问题的核心。
不管是经典力学还是量子力学梯度对应的是空间动量,旋度对应的是空间角动量。
所有矢量都可以化为梯度场和旋度场。此即霍姆赫兹定理。梯度场的旋度为零,对应动量守恒。旋度场的散度为零,对应角动量守恒。
(6)流体力学
Divergence(散度)和Curl(旋度)的主要作用目前看来好像就是方便积分,其中Divergence Theorem和Stokes Theorem可以转化散度和旋度的复杂的积分到简单一点的形式。(其实也不是每一个转了之后都变得更好的)
物理上的理解也许采用流体力学的版本较好,一个点的散度测量水流流进和流出这个点的速率,一个点的旋度测量这个点水流旋转的快慢。
参考:知乎解答
















 Python基础 (三))


)