我们比较熟悉的不等式可能就是下面的这个不等式链以及柯西不等式了：

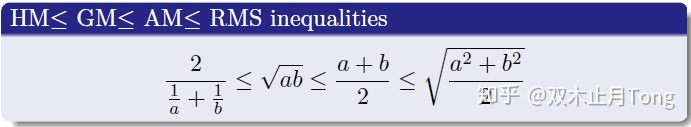
对于不等式链的证明我们可以看下面这张图，非常直观形象：

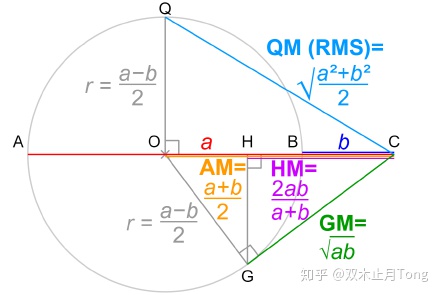
不太懂得也可以看这个视频讲解：

知乎视频​www.zhihu.com

对于柯西不等式的证明及讲解，我们之前也分享过：

https://zhuanlan.zhihu.com/p/107477843​zhuanlan.zhihu.com

今天我们主要是来分享一下三个不太用到的不等式：排序不等式、切比雪夫不等式以及伯努利不等式，接下去我们分别来介绍及证明一下。

一、排序不等式Rearrangement Inequality

之前上课有个学生看到

哈哈，是的，不过这里指的是一个置换，就是把下标（*）换成其它数字。

上面的形式概括一下就是：顺序和≥乱序和≥倒序和

接下去证明一下：

【证明】

先证明顺序和≥乱序和

假设

如果说

不然，至少存在一个

接着，我们可以分析出来必定存在一个

因为

于是，

也就是说，我们可以通过交换

与假设矛盾，

类似的方法我们也可以用来证明乱序和≥倒序和，大家可以试一下。

放个简单例题试试手：

Question:

二、切比雪夫不等式Chebyshev's Inequality

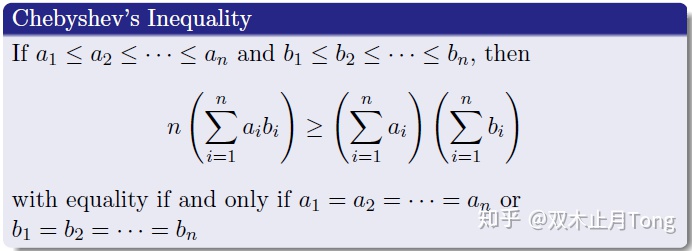
切比雪夫不等式可以通过排序不等式能够很快得到，不等式左边是n个顺序和，那么不等式的右边是什么，可能这样不太直观，我们把它写成矩阵形式来看看：

其实是1个顺序和+n-1个乱序和，简单的画两条线大家就看清楚了：

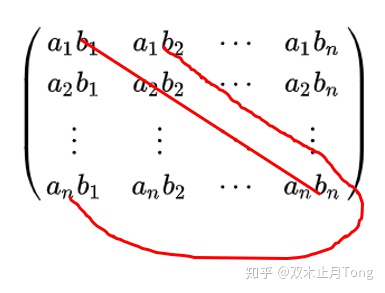
三、伯努利不等式Bernoulli's Inequality

可以借助数学归纳法来证明伯努利不等式，下面简单写一下：

【证明】

当

假设当

当

因为

下面也给一道关于伯努利不等式的简单习题，有兴趣可以做一下：

Question:

---

至此，我们就分享完了排序不等式，切比雪夫不等式及伯努利不等式及它们的证明，说实话在国际数学竞赛中，比如AMC10/12等，是不太用到的，最重要(最常考)的还是前面的基本不等式以及柯西不等式了。所以，后面的就了解一下，哪天见到了有点印象就可以啦:D

本文就介绍到这里了，欢迎交流指正，感觉还可以的不要忘记点个赞呀！

总感觉干货好像不太受欢迎?_?

想了解更多国际数学竞赛的知识，可参阅：

https://zhuanlan.zhihu.com/p/62918360​zhuanlan.zhihu.com