解题思路:

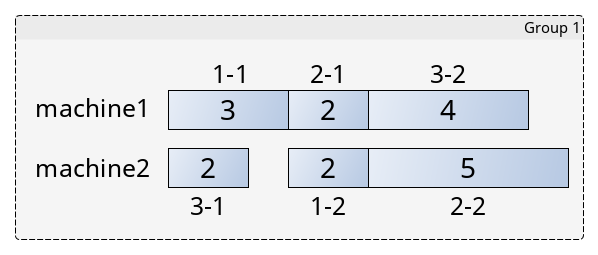
如图所示，对于第一组样例输入，按照总工序提供的顺序，对于每个工件的工序从小到大，每次寻找有空闲机器的“空档”插入，就能让总加工时间最短。

注意事项:

按照约定，最短方案有且只有一种。

参考代码:#include

int w[21];                                    //当前安排的工件处于几号工序

int u[501];                                   //安排几号工件进入总工序

int lt[21];                                   //当前安排的工件几时结束

int t[21][21];                                //每个工件的每个工序的加工时间

int d[21][21];                                //每个工件的每个工序所使用的机器号

int c[21][501];                               //每个机器在工件完成后某时间段内是否被占用

int main(){

int max(int,int);

int i,j,k,m,n,ans=0,s=0;

scanf("%d%d",&m,&n);

for(i=1;i<=m*n;i++) scanf("%d",&u[i]);    //输入总工序

for(i=1;i<=n;i++)

for(j=1;j<=m;j++)

scanf("%d",&d[i][j]);             //输入第1个工件第j个工序所使用的机器号

for(i=1;i<=n;i++)

for(j=1;j<=m;j++)

scanf("%d",&t[i][j]);             //输入第i个工件第j个工序的加工时间

for(i=1;i<=n*m;i++){

w[u[i]]++;                            //总工序中第i个工件处于几号工序

for(j=lt[u[i]]+1;;j++){               //总工序中工件u[i]当前工序若能完成的时间段

if(c[d[u[i]][w[u[i]]]][j]==0) s++;//工件u[i]在当前工序所使用的机器未被占用时长

else s=0;

if(s==t[u[i]][w[u[i]]]){          //工件u[i]在当前工序的加工时间

for(k=j-s+1;k<=j;k++)         //在j之前的这段时间s

c[d[u[i]][w[u[i]]]][k]=1; //安排工件u[i]在当前工序占用相应的机器

lt[u[i]]=j;                   //工件u[i]的完成时间

s=0;

break;

}

}

}

for(i=1;i<=n;i++)

ans=max(ans,lt[i]);                   //工序中最后一个工件的完成时间

printf("%d",ans);

return 0;

}

int max(int a,int b){

return a>b?a:b;

}