有十五个数按由大到小顺序存放在一个数组中_数据结构基础 (代码效率优化, 线性表, 栈, 队列, 数组，字符串，树和二叉树，哈希表)...

作者：张人大

代码效率优化

复杂度 -- 一个关于输入数据量n的函数

时间复杂度 -- 昂贵
- 与代码的结构设计有着紧密关系
- 一个顺序结构的代码，时间复杂度是O(1), 即任务与算例个数 n 无关
空间复杂度 -- 廉价
- 与数据结构设计有关

数据结构 -- 考虑如何去组织计算机中一定量的数据。

数据结构连接时空，用空间换取时间。

数据处理 -- 了解问题，明确数据操作方法，设计出更加高效的数据结构类型

找到需要处理的数据，计算结果，再把结果保存下来
- 把结果存到新的内存空间中
- 把结果存到已使用的内存空间中
基本操作只有三个：增，删，查
- 增和删可以细分为数据结构的中间以及最后的增和删
- 查找可以细分为按照位置条件查找和数据数值特征查找
- 所有数据处理都是这些基本操着的组合和叠加
只有字典类型数据结构能在 O(1) 的时间复杂度内完成查找动作
回归问题本源，明确数据被处理的动作，来解决数据结构的问题

想了解更多，欢迎关注我的微信公众号：Renda_Zhang

线性表

n 个具有相同特性的元素的有限序列，Linear List

数据元素之间的关系是一对一的关系

即除了头尾元素外，其它数据元素都是首尾相接的
- 这句话只适用大部分线性表，而不是全部
- 比如，循环链表尾的指针指向首位结点

实现方式

最常用的是链式表达，也叫线性链表或链表
- 每个结点包括具体的数据值和指向下一个结点的指针
- 单向链表，循环链表，双向链表，双向循环链表
- 新增和删除为 O(1) 时间复杂度，而查找为 O(n)
- 适合数据元素个数不确定，且经常进行新增和删除
- 链表的翻转，快慢指针的方法，是必须掌握的内容
使用数组实现，也叫顺序存储，顺序表

类别

一般线性表，可以自由的删除和添加结点
受限线性表，主要包含栈和队列

栈和队列是特殊的线性表，本质上他们都可以被看作是一类基本结构

线性表案例

链表的翻转
快慢指针
- 查找奇数个数的链表的中间位置结点的数值
- 判断链表是否有环

栈

后进先出的（限制后的）线性表，Last In First Out, Stack.

新增和删除操作只能在这个线性表的表尾进行，即在线性表基础上加了限制

新增: 压栈 push, which adds an element to the collection
删除: 出栈 pop, which removes the most recently added element

功能上，数组或者链表可以代替栈，但它们灵活性过高，数据量大时有风险

栈顶和栈底是用来表示这个栈的两个指针

栈顶 (top) 是表尾，用来输入数据
栈底 (bottom) 是表头

栈有顺序表示和链式表示，分别称作顺序栈和链栈

顺序栈
- 可以借助数组来实现
  - 数组的首元素存在栈底，尾元素放在栈顶
  - 定义指针 top 来指示栈顶元素在数组的位置
- 栈中只有一个元素，则 top = 0
- 以 top 是否为 -1 来判定是否为空栈
- 栈顶 top 需小于栈的最大容量
- 出栈操作，只需要 top - 1 即可
链式栈
- 用链表的方式实现
  - 通常把栈顶放在单链表的头部
  - top 指针替换了链表原来的尾指针，去掉了头指针
- 出栈操作，将 top 指针指向栈顶元素的 next 指针即可
对比栈和一般线性表
- 相同点：
  - 操作原理相似
  - 时间复杂度一样
  - 都依赖当前位置指针进行数据对象的操作
- 区别：栈只能新增和删除栈顶的数据结点

栈的案例

判断括号字符串是否合法
浏览器页面访问的后退和前进

队列

先进先出 (限制后的) 线性表, First In First Out, Queue

新增和删除操作只能分别在队尾和队头进行

先进 - 队列的数据新增操作只能在末端进行, add
- 不允许在队列的中间某个结点后新增数据
先出 - 队列的数据删除操作只能在始端进行, remove
- 不允许在队列的中间某个结点后删除数据

队列适合面对数据处理顺序非常敏感的问题

可以确定队列长度最大值, 建议使用循环队列
无法确定队列长度时, 应考虑使用链式队列

front 和 rear 两个指针

队头 (front), 用来删除数据
队尾 (rear), 用来增加数据

队列有两种存储方式, 即顺序队列和链式队列

顺序队列
- 依赖数组来实现
  - 数据在内存中也是顺序存储
- 进行新增插入操作时,
  - 尾指针会向后移动
  - 时间复杂度为 O(1)
- 如果只删除头的第一个元素时
  - 每次删除都需要把整个数组前移
  - 时间复杂度为 O(n)
- 使用循环队列
  - 必须有一个固定的长度
  - 实现删除的时间复杂度为 O(1)
  - 使用 flag 来判断队列空或满
链式队列
- 依赖链表来实现
  - 数据依赖每个结点的指针互联
  - 是离散存储线性结构
  - 实际上就是尾进头出的单链线性表
  - 在空间上更为灵活
- 通常会增加一个头结点
  - 让 front 指针指向头结点
  - 头结点不存储数据, 只是辅助标识
- 当进行数据删除时, 实际删除的是头结点的后继结点
- 队列为空时, 头尾指针都指向头结点
对比队列和一般线性表
- 队列继承了线性表的优点和不足
- 是加了限制的线性表

队列案例

约瑟夫环 - Josephus problem

数组

数组可以看成是线性表的一种推广，它属于另外一种基本的数据结构

数组是数据结构中的最基本结构

几乎所有的程序设计语言都把数组类型设定为固定的基础变量类型。
可以把数组理解为一种容器，它可以用来存放若干个相同类型的数据元素。
例如：
- 存放的数据是整数型的数组，称作整型数组；
- 存放的数据是字符型的数组，则称作字符数组；
- 另外还有一类数组比较特殊，它是数组的数组，也可以叫作二维数组。
可以把普通的数组看成是一个向量，那么二维数组就是一个矩阵。
数组在内存中是连续存放的，数组内的数据，可以通过索引值直接取出得到。

数组的索引就是对应数组空间

在进行新增、删除、查询操作的时候，完全可以根据代表数组空间位置的索引值进行。
只要记录该数组头部的第一个数据位置，然后累加空间位置即可。

数组的基本操作

具有增删困难、查找容易的特点，可以在任意位置增删数据，所以数组的增删操作会更为多样。

新增操作
- 若插入数据在最后，则时间复杂度为 O(1)
- 如果中间某处插入数据，则时间复杂度为 O(n)
删除操作
- 在数组的最后删除一个数据元素，则时间复杂度是 O(1)
- 在这个数组的中间某个位置删除一条数据, 时间复杂度为 O(n)
查找操作
- 如果只需根据索引值进行一次查找，时间复杂度是 O(1)
- 要在数组中查找一个数值满足指定条件的数据，则时间复杂度是 O(n)。

对比数组和链表

链表的长度是可变的，数组的长度是固定的，在申请数组的长度时就已经在内存中开辟了若干个空间。如果没有引用 ArrayList 时，数组申请的空间永远是我们在估计了数据的大小后才执行，所以在后期维护中也相当麻烦。
链表不会根据有序位置存储，进行插入数据元素时，可以用指针来充分利用内存空间。数组是有序存储的，如果想充分利用内存的空间就只能选择顺序存储，而且需要在不取数据、不删除数据的情况下才能实现。

数组的案例

基于数组，计算平均值

字符串

由 n 个字符组成的一个有序整体（ n >= 0 ）

对比字符串和线性表

字符串的逻辑结构和线性表极为相似，区别仅在于串的数据对象约束为字符集。
字符串的基本操作和线性表有很大差别：
- 在线性表的基本操作中，大多以“单个元素”作为操作对象；
- 在字符串的基本操作中，通常以“串的整体”作为操作对象；
- 字符串的增删操作和数组很像，复杂度也与之一样。但字符串的查找操作就复杂多了，它是参加面试、笔试常常被考察的内容。

特殊的字符串

空串，指含有零个字符的串。例如，s = ""，书面中也可以直接用 Ø 表示。
空格串，只包含空格的串。它和空串是不一样的，空格串中是有内容的，只不过包含的是空格，且空格串中可以包含多个空格。例如，s = " "，就是包含了 3 个空格的字符串。
子串，串中任意连续字符组成的字符串叫作该串的子串。
原串通常也称为主串。

字符串的存储结构与线性表相同，也有顺序存储和链式存储两种

字符串的顺序存储结构，是用一组地址连续的存储单元来存储串中的字符序列，一般是用定长数组来实现。有些语言会在串值后面加一个不计入串长度的结束标记符，比如 0 来表示串值的终结。
字符串的链式存储结构，与线性表是相似的，但由于串结构的特殊性（结构中的每个元素数据都是一个字符），如果也简单地将每个链结点存储为一个字符，就会造成很大的空间浪费。因此，一个结点可以考虑存放多个字符，如果最后一个结点未被占满时，可以使用 "#" 或其他非串值字符补全。
- 每个结点设置字符数量的多少，与串的长度、可以占用的存储空间以及程序实现的功能相关。
- 除了在连接串与串操作时有一定的方便之外，不如顺序存储灵活，在性能方面也不如顺序存储结构好。

字符串的基本操作

新增操作
- 和数组非常相似，都牵涉对插入字符串之后字符的挪移操作，所以时间复杂度是 O(n)。
- 对于特殊的插入操作时间复杂度也可以降低为 O(1)。例如，在 s1 的最后插入 s2，也叫作字符串的连接。
删除操作
- 和数组同样非常相似，也可能会牵涉删除字符串后字符的挪移操作，所以时间复杂度是 O(n)。
- 对于特殊的删除操作时间复杂度也可以降低为 O(1)。例如，在 s1 的最后删除若干个字符，不牵涉任何字符的挪移。
查找操作
- 子串查找（字符串匹配）
  - 在字符串 A 中查找字符串 B，则 A 就是主串，B 就是模式串。
  - 主串的长度记为 n，模式串长度记为 m，则n>m。
  - 字符串匹配算法的时间复杂度就是 n 和 m 的函数。

字符串匹配算法的案例

查找出两个字符串的最大公共字串

树和二叉树

树 -- Tree

树结构在存在“一对多”的数据关系中，可被高频使用，这也是它区别于链表系列数据结构的关键点。
树是由结点和边组成的，不存在环的一种数据结构。
树满足递归定义的特性。如果一个数据结构是树结构，那么剔除掉根结点后，得到的若干个子结构也是树，通常称作子树。
树的结点的层次从根结点算起，根为第一层，根的“孩子”为第二层，根的“孩子”的“孩子”为第三层，依此类推。
树中结点的最大层次数，就是这棵树的树深（称为深度，也称为高度）。

二叉树 -- Binary Tree

二叉树每个结点最多有两个子结点，分别称作左子结点和右子结点。

二叉树中两个特殊的类型

满二叉树，定义为除了叶子结点外，所有结点都有 2 个子结点。
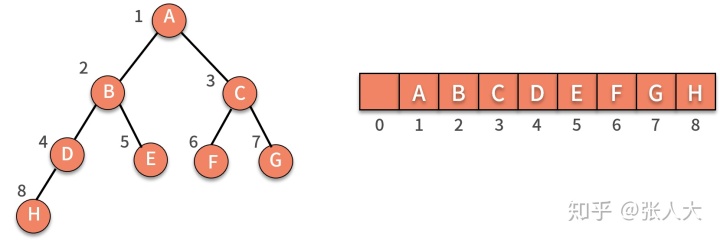
完全二叉树，定义为除了最后一层以外，其他层的结点个数都达到最大，并且最后一层的叶子结点都靠左排列。它方便了顺序存储法的存储方式。

存储二叉树的两种办法

链式存储法，也就是像链表一样，每个结点有三个字段，一个存储数据，另外两个分别存放指向左右子结点的指针。
顺序存储法，就是按照规律把结点存放在数组里。如图所示。

树的基本操作

遍历

前序遍历，对树中的任意结点来说，先打印这个结点，然后前序遍历它的左子树，最后前序遍历它的右子树。
public static void preOrderTraverse(Node node) {
if (node == null)
return;
System.out.print(node.data + " ");
preOrderTraverse(node.left);
preOrderTraverse(node.right);
}
中序遍历，对树中的任意结点来说，先中序遍历它的左子树，然后打印这个结点，最后中序遍历它的右子树。
public static void inOrderTraverse(Node node) {
if (node == null)
return;
inOrderTraverse(node.left);
System.out.print(node.data + " ");
inOrderTraverse(node.right);
}
后序遍历，对树中的任意结点来说，先后序遍历它的左子树，然后后序遍历它的右子树，最后打印它本身。
public static void postOrderTraverse(Node node) {
if (node == null)
return;
postOrderTraverse(node.left);
postOrderTraverse(node.right);
System.out.print(node.data + " ");
}

二叉树的增删查操作很普通，时间复杂度与链表并没有太多差别

二叉查找树 -- Binary Search Tree, BST

特性

在二叉查找树中的任意一个结点，其左子树中的每个结点的值，都要小于这个结点的值。
在二叉查找树中的任意一个结点，其右子树中每个结点的值，都要大于这个结点的值。
在二叉查找树中，会尽可能规避两个结点数值相等的情况。
对二叉查找树进行中序遍历，就可以输出一个从小到大的有序数据队列。

查找操作 -- 利用了“二分查找”，所消耗的时间复杂度为 `O(logn)`。

首先判断根结点是否等于要查找的数据，如果是就返回。
如果根结点大于要查找的数据，就在左子树中递归执行查找动作，直到叶子结点。
如果根结点小于要查找的数据，就在右子树中递归执行查找动作，直到叶子结点。

插入操作

插入操作很简单。从根结点开始，如果要插入的数据比根结点的数据大，且根结点的右子结点不为空，则在根结点的右子树中继续尝试执行插入操作。直到找到为空的子结点执行插入动作。
二叉查找树插入数据的时间复杂度是 O(logn)。这里的时间复杂度更多是消耗在了遍历数据去找到查找位置上，真正执行插入动作的时间复杂度仍然是 O(1)。

删除操作

情况一，如果要删除的结点是某个叶子结点，则直接删除，将其父结点指针指向 null 即可。
情况二，如果要删除的结点只有一个子结点，只需要将其父结点指向的子结点的指针换成其子结点的指针即可。
情况三，如果要删除的结点有两个子结点，则有两种可行的操作方式：
- 第一种，找到这个结点的左子树中最大的结点，替换要删除的结点。
- 第二种，找到这个结点的右子树中最小的结点，替换要删除的结点。

树的案例

字典树 -- Dictionary Tree

第一，根结点不包含字符；
第二，除根结点外每一个结点都只包含一个字符；
第三，从根结点到某一叶子结点，路径上经过的字符连接起来，即为集合中的某个字符串。

哈希表

哈希表 -- Hash Table, 也叫作散列表。

哈希表是一种特殊的数据结构，它与数组、链表以及树等我们之前学过的数据结构相比，有很明显的区别。

线性表中的栈和队列对增删有严格要求，它们会更关注数据的顺序。
数组和字符串需要保持数据类型的统一，并且在基于索引的查找上会更有优势。
树的优势则体现在数据的层次结构上。
哈希表优势体现在，无论有多少数据，查找、插入、删除只需要接近常量的时间，即 O(1）的时间级。

核心思想

实现 “地址 = f (关键字)” 的映射关系，快速完成基于数据的数值的查找。

哈希函数的设计

直接定制法

哈希函数为关键字到地址的线性函数。如，H (key) = a*key + b。这里，a 和 b 是设置好的常数。

数字分析法

假设关键字集合中的每个关键字 key 都是由 s 位数字组成（k1,k2,…,Ks），并从中提取分布均匀的若干位组成哈希地址。

平方取中法

如果关键字的每一位都有某些数字重复出现，并且频率很高，我们就可以先求关键字的平方值，通过平方扩大差异，然后取中间几位作为最终存储地址。

折叠法

如果关键字的位数很多，可以将关键字分割为几个等长的部分，取它们的叠加和的值（舍去进位）作为哈希地址。

除留余数法

预先设置一个数 p，然后对关键字进行取余运算。即地址为 key mod p。

解决哈希冲突

开放定址法

常用的探测方法是线性探测法。比如有一组关键字 {34，35，36，45}，采用的哈希函数为 key mod 11。当插入 34，35，36 时可以直接插入，地址分别为 1、2、3。而当插入 45 时，哈希地址为 45 mod 11 = 1。然而，地址 1 已经被占用，因此沿着地址 1 依次往下探测，直到探测到地址 4，发现为空，则将 45 插入其中。