什么是关键路径法CPM?
关键路径法用于在进度模型中估算项目最短工期,确定逻辑网络路径的进度灵活性大小。这种进度网络分析技术在不考虑任何资源限制的情况下,沿进度网络路径使用顺推与逆推法,计算出所有活动的最早开始ES、最早结束EF、最晚开始LS和最晚完成LF日期。
由此得到的最早和最晚的开始和结束日期并不一定就是项目进度计划,而只是把既定的参数(活动持续时间、逻辑关系、提前量、滞后量和其他已知的制约因素)输入进度模型后所得到的一种结果,表明活动可以在该时段内实施。
什么是关键路径?
- 关键路径是项目中时间最长的活动顺序,决定着可能的项目最短工期。
- 计算关键路径的长度时,需要将路径上的所有活动的持续时间、提前量(负的)和滞后量(正的)加总在一起。
- 最长路径的总浮动时间最少,通常为零;进度网络图可能有多条关键路径。
- 长度仅次于关键路径的路径称为次关键路径,次关键路径也可能有多条。
- 借助进度计划软件来规划时,为了达成相关方的限制要求,可以自行定义用于确定关键路径的参数。
关键路径法的作用
关键路径法用来计算进度模型中的关键路径、总浮动时间和自由浮动时间,或逻辑网络路径的进度灵活性大小。
最早时间和最晚时间
- 最早开始结束时间
ES:最早开始时间(Earliest Start),是指某项活动能够开始的最早时间,只决定于项目计划,只要计划的条件满足了就可以开始的时间。
EF:最早结束时间(Earliest Finish),是指某项活动能够完成的最早时间。
其中EF = ES+DU, DU为活动持续时间,顺推法先知道开始时间。
- 最晚结束和开始时间
LF:最迟结束时间(Latest Finish),是指为了使项目在要求完工时间内完成,某项活动必须完成的最迟时间。往往决定于相关方(客户或管理层)的限制。
LS:最迟开始时间(Latest Start),是指为了使项目在要求完工时间内完成,某项活动必须开始的最迟时间
其中LS = LF -DU,DU为持续时间,逆推法先知道结束时间。
- 图形表示
按照《PMBOK指南》的推荐,采用图6-24的方式来标注活动的ES、EF、DU、LF、LS以及活动名称(ID)
图6-24

@提示
在考试中未必需要把图6-24的格子画出来,只需要按照图中的方位进行标注就可以了,这样做的好处时在计算TF和FF时不容易出错。TF和FF的计算方法参见本节后续内容。
活动从第0天开始还是从第1天开始
采用顺推法和逆推法进行进度网络路径计算时,需要关注活动是从第0天开始还是从第1天开始,不同的假设计算的结果是不一样的。首先需要明确以下几个概念。
- 活动的持续时间DU是指活动的工作时间段,例如一个活动持续时间是24小时,是指3个工作日(每天8小时)。
- 活动的开始时间是指活动开工日的上班开始时间;活动结束是指开工日的下班时间。也就是说假设一个活动的持续时间是2天,是指从第1天上班时间,到第2天下班时间的所有工作时间段。
所谓活动从第0天还是第1天开始,意思是说要不要把活动开始的那一天计算在工作时间段内。因为现实中第0天是不存在的,所以活动开始的那一天就不需要计算在内;而活动从第1天开始,由于第1天是存在的,就需要计算在工作时间段内。这两种情况导致当前活动的EF或者LS,紧后活动的ES和LF在计算时要考虑是否减去或加上这1天的问题。
无论是从第0天开始,还是第1天开始,都不会影响关键路径的和浮动时间的计算方法,但是考试中如果弄错了则会影响计算结果,考试中为了简化计算通常采用第0天开始,现实中为了与实际日历日期相符合通常采用第1天开始。下面就这两种方式举例说明。

第一种情况:活动从第0天开始,如图6-25
图6-25
计算公式如下:
对于当前活动:顺推时 EF = ES + DU; 逆推时 LS= LF – DU
对于紧后活动:顺推时ESi= EFi-1, ;顺推时LFi-1 = LS i (例如逆推时活动C相当于活动D的紧后活动)
其中自左向右,“i”代表当前活动,则“i-1”代表“i”的紧前活动。
例如,
对于活动A、B的最早时间, EFA = ESA+DU = 0+5 = 5,ESB = EFA = 5;
对于活动D和C的最晚时间,LSD = LFD – DU = 30 -15 =15,LFC = LSD = 15;
第二种情况:活动从第1天开始,如图6-26
对于当前活动:顺推时 EF = (ES + DU)-1; 逆推时 LS =(LF – DU)+1
对于紧后活动:顺推时ESi= EFi-1 +1 ;逆推时LFi-1 = LS i -1
其中自左向右,“i”代表当前活动,则“i-1”代表“i”的紧前活动。
例如,
对于活动A、B的最早时间, EFA = ESA+DU-1 = 1+5-1 = 5,ESB = EFA +1= 5+1 = 6;

对于活动D和C的最晚时间,LSD = LFD – DU+1 = 30 -15 +1 =16,LFC = LSD -1 = 15;
图6-26
@提示
从上两种计算方法来看,活动从第0天开始显然对人工计算来说更加直观简便,这种方法的缺点是与日历日期的对应关系是不一致的。活动从第1天开始计算的结果与日历日期是一致的,但是计算过程是不直观的。好在考试中一般不会涉及具体的日历日期,所以推荐使用活动从第0天开始的计算方法。
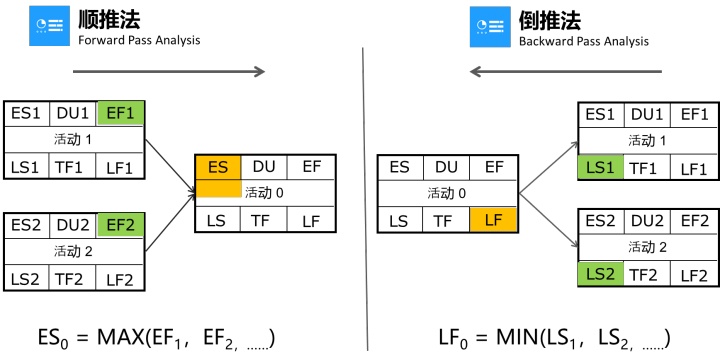
顺推法与逆推法
图6-27
自左向右计算最早时间称为顺推;自右向左计算最晚时间称为逆推。
在顺推时会出现如图6-27(左)的情况,即当前活动有两个和两个以上的紧前活动,那么当前活动的ES的取值应该遵循顺推取最大的原则,即ES0 = MAX(EF1,EF2,……)。
在逆推时也会出现如图6-27(右)的情况,即当前活动有两个和两个以上的紧后活动,那么当前活动的ES的取值应该遵循逆推取最小的原则,即ES0 = MIN(EF1,EF2,……)。
@提示
顺推法得到的最早工期代表项目期望的计划工期;逆推法时设定的最晚工期代表相关方的期望工期。
总浮动时间TF
- 定义:在任一网络路径上,进度活动可以从最早开始日期推迟或拖延的时间,而不至于延误项目完成日期或违反进度制约因素,就是总浮动时间或进度灵活性。
- 取值:在进行紧前关系绘图法排序的过程中,取决于所用的制约因素,关键路径的总浮动时间可能是正值、零或负值。
- 总浮动时间为正值,是由于逆推计算所使用的进度制约因素要晚于顺推计算所得出的最早完成日期,即给定的工期比计划的工期要长。
- 总浮动时间为负值,是由于持续时间和逻辑关系违反了对最晚日期的制约因素,即给定的工期要比计划的工期要短。

计算方法:TF = LS – ES = LF – EF,即按照图6-28箭头所示的方向求值。
图6-28
负值浮动时间分析
- 关键路径出现负的浮动时间意味着,如果不采取措施项目将延期。
- 负值浮动时间分析是一种有助于找到推动延迟的进度回到正轨的方法的技术,从而找到保证工期的途径。
- 为了使网络路径的总浮动时间为零或正值,可能需要调整活动持续时间(可增加资源或缩减范围时)、逻辑关系(针对选择性依赖关系时)、提前量和滞后量,或其他进度制约因素。
自由浮动时间FF
- 自由浮动时间就是指在不延误任何紧后活动最早开始日期或不违反进度制约因素的前提下,某进度活动可以推迟的时间量。
- 总浮动时间可能等于大于自由浮动时间,TF≥FF。

计算方法,如图6-29所示
图6-29
对于图6-29(左)的情况:活动0的FF0 = ES1 – EF0
对于图6-29(右)的情况:活动0的FF0 = MIN{ (ES1 – EF0), (ES2-EF0) ,……}
@提示
由于自由浮动时间的计算涉及前后活动之间的参数不容易记忆,只要记住图6-29所示的计算方式就不容易搞错了。
项目浮动
一个项目可以延误但不影响外界(如客户或发起人)限制的完工日期的时间。例如客户要求11.11号完工,项目团队的计划是在11.1完工,那么二者之间就有10天的浮动时间;如果按照客户要求日期完工,则项目浮动会反映在总浮动时间上。
关键路径常见考点小结,请参考表6-7。
表6-7

关键路径法完整的计算示例
请计算如表6-8所列活动的关键路径,并完成顺推计算最早时间和逆推计算最晚时间,计算所有活动的TF和活动C的自由浮动时间FF。

表6-8
第一步,画出网络图,如图6-30(1)
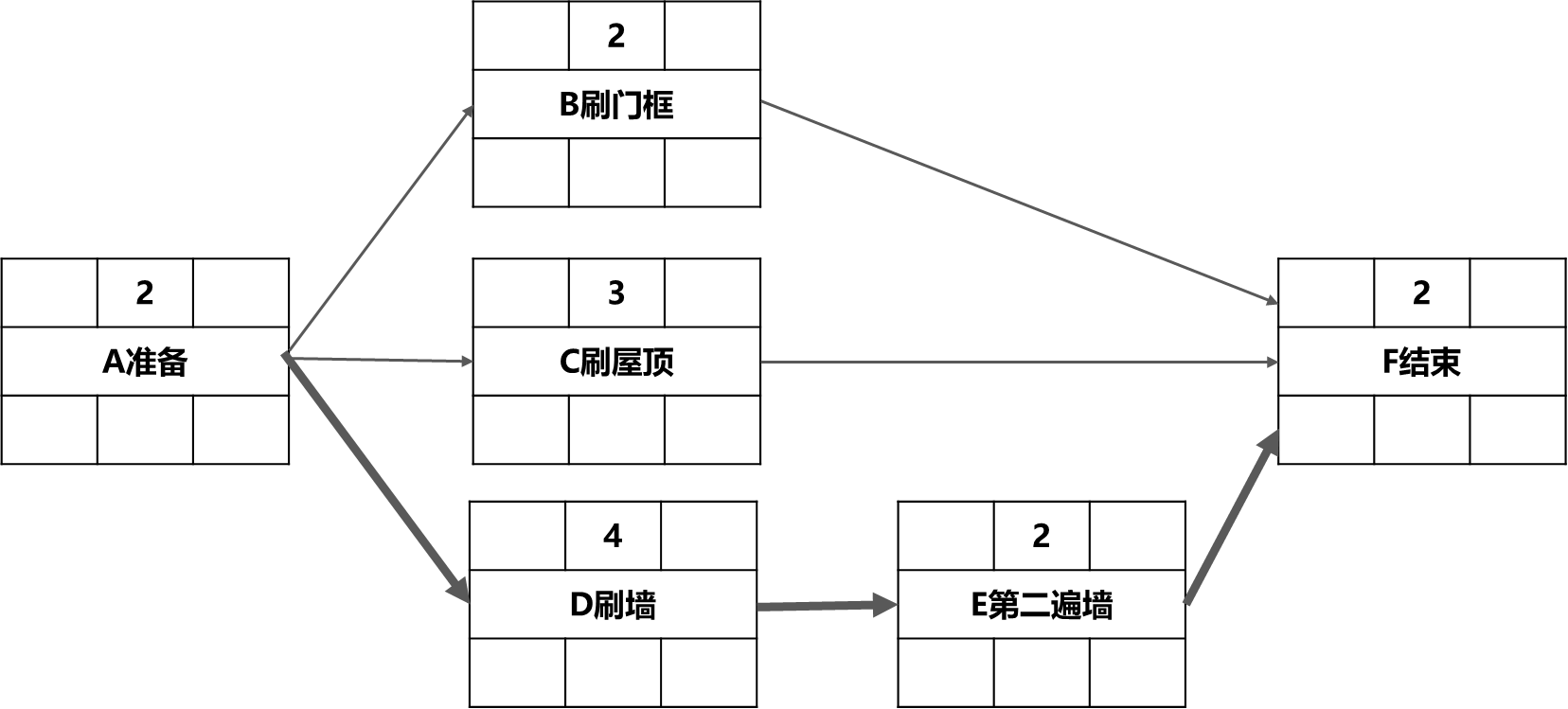
图6-30(1)
第二步:计算关键路径,列出所有可能的路径,比较其长度
- 路径A-B-F长度为2+2+2 = 6
- 路径A-C-F长度为2+3+2 = 7
- 路径A-D-E-F长度为2+4+2+2 = 10
故关键路径为A-D-E-F,长度为10
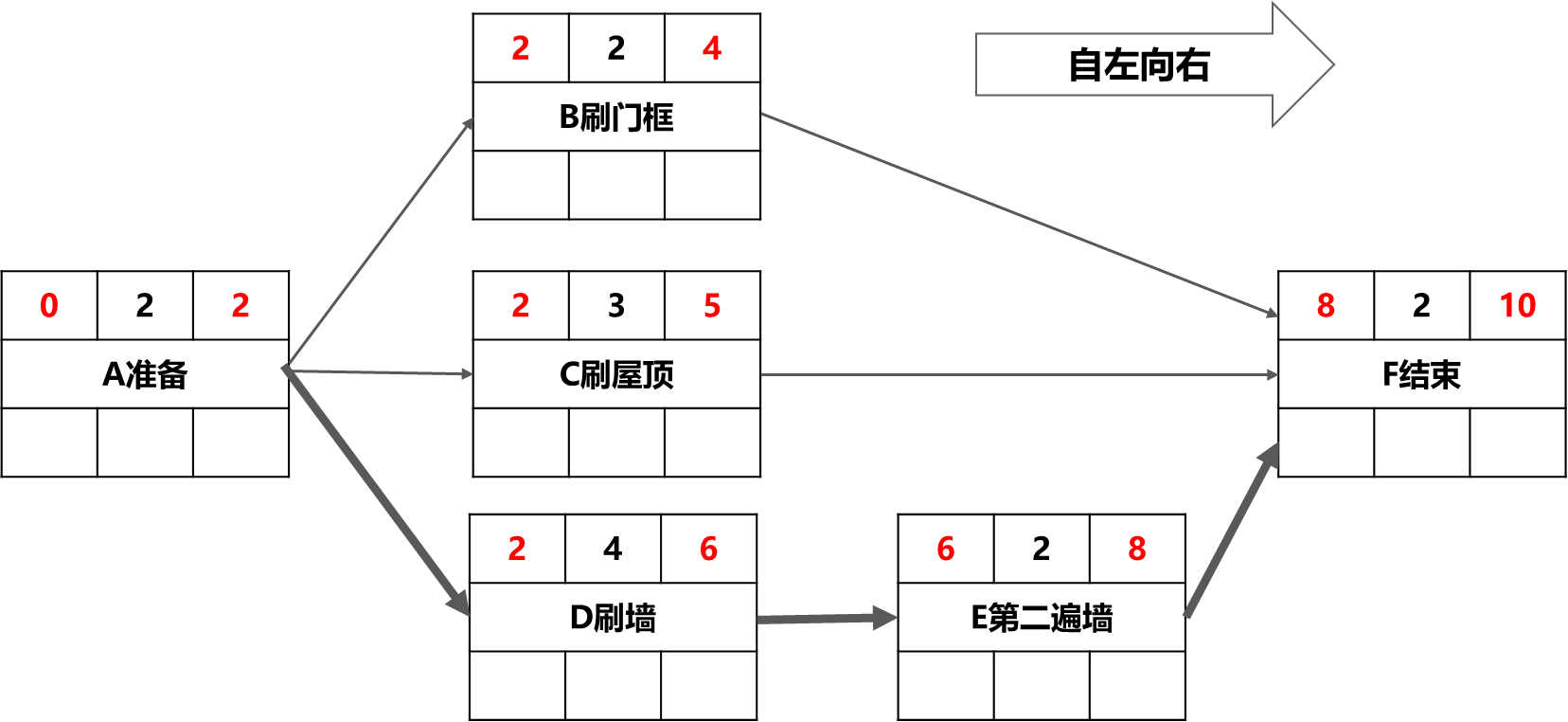
第三步:顺推计算最早时间,按照从第0天开始,如图6-30(2)
图6-30(2)
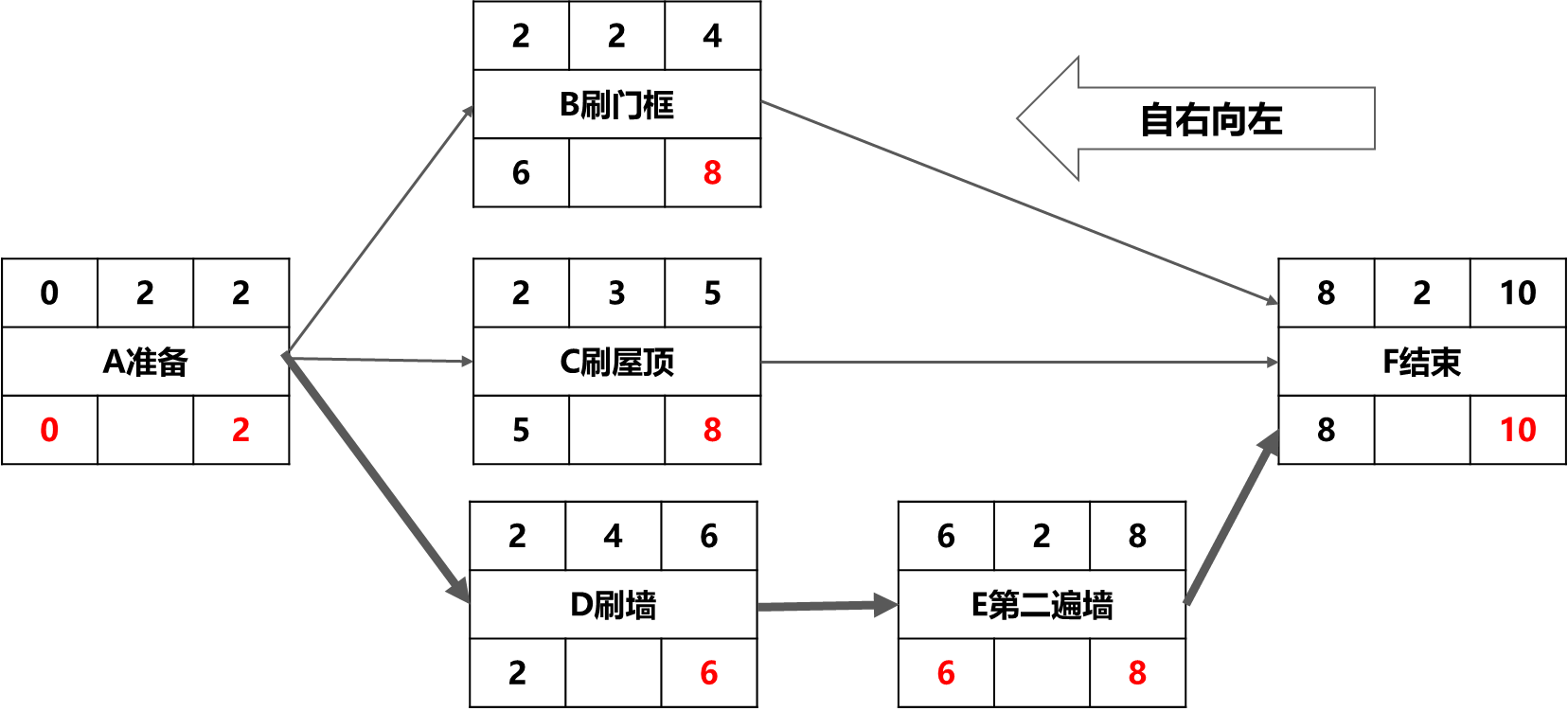
第四步:逆推计算最晚时间,如图6-30(3)
图6-30(3)
第五步,计算所有活动的TF和活动C的FF,如图6-30(4)所示。
活动C的FF为:FFc = ESF-EFc = 8 – 5 = 3

6-30(4)
原创:陈利海
原载:易解项目管理(EasyPMP)
)

)







,将数字转换成字符(itoa))
|实用技巧之Word篇)







