【力扣】77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按任何顺序返回答案。

示例 1：
输入：n = 4, k = 2
输出：

[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]

示例 2：
输入：n = 1, k = 1
输出：

[[1]]

提示：
1 <= n <= 20
1 <= k <= n

题解

暴力思考：k 等于多少就是多少层循环。

//示例中k为2
int n = 4;
for (int i = 1; i <= n; i++) {for (int j = i + 1; j <= n; j++) {	sout(i+" "+j);}
}//示例中k为3
int n = 100;
for (int i = 1; i <= n; i++) {for (int j = i + 1; j <= n; j++) {for (int u = j + 1; u <= n; n++) {sout(i+" "+j+" "+u);}}
}

回溯

回溯法解决的问题都可以抽象为树形结构（N叉树）。

n 相当于树的宽度，k 相当于树的深度。图中每次搜索到了叶子节点，就找到了一个结果。

回溯法三步

• 递归函数的返回值以及参数

• 回溯函数终止条件

• 单层搜索的过程

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}

import java.util.*;public class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {backtracking(n, k, 1);return result;}public void backtracking(int n, int k, int startIndex) {// 终止条件if (path.size() == k) {//存放结果result.add(new ArrayList<>(path));return;}//横向遍历for (int i = startIndex; i <= n; i++) {//处理节点path.add(i);//纵向搜索backtracking(n, k, i + 1);//回溯，撤销处理结果path.removeLast();}}
}

剪枝优化

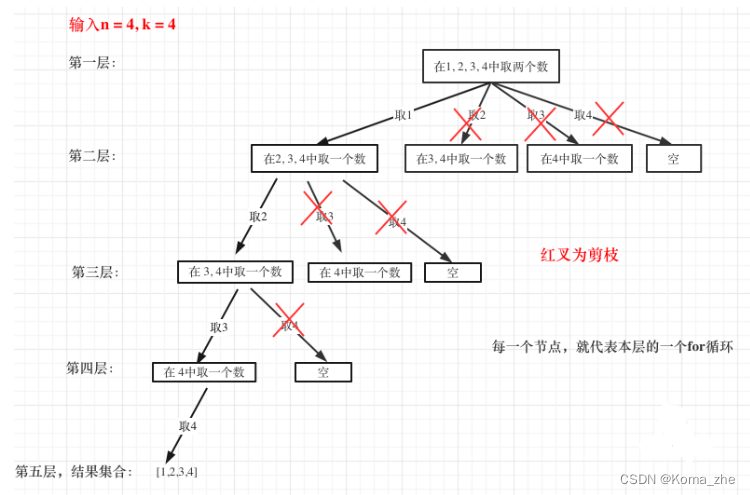
剪枝的地方就在递归中每一层的for循环所选择的起始位置。如果 for 循环选择的起始位置之后的元素个数已经不足需要的元素个数，那么就没有必要搜索了。

• 已经选择的元素个数：path.size();
• 还需要的元素个数为: k - path.size();
• 在集合 n 中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

import java.util.*;public class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {backtracking(n, k, 1);return result;}public void backtracking(int n  , int k, int startIndex) {// 终止条件if (path.size() == k) {//存放结果result.add(new ArrayList<>(path));return;}//横向遍历for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) {// i为本次搜索的起始位置//处理节点path.add(i);//纵向搜索backtracking(n, k, i + 1);//回溯，撤销处理结果path.removeLast();}}
}