系列简介：这个系列文章讲解线性代数的基础内容，注重学习方法的培养。线性代数课程的一个重要特点(也是难点)是概念众多，而且各概念间有着千丝万缕的联系，对于初学者不易理解的问题我们会不惜笔墨加以解释。在内容上，以国内的经典教材“同济版线性代数”为蓝本，并适当选取了一些补充材料以开阔读者的视野。本系列文章适合作为初学线性代数时的课堂同步辅导，也可作为考研复习的参考资料。文章中的例题大多为扎实基础的常规题目和帮助加深理解的概念辨析题，并有相当数量的历年考研试题。对于一些难度较大或对理解所学知识有帮助的“经典好题”，我们会详细讲解。“线性代数入门”系列文章，欢迎关注数学若只如初见！

上一节中我们介绍了一类重要行列式的计算方法，n阶行列式的计算是线性代数中难度较大的一类题目，技巧性较强，本节我们再介绍另外一类n阶行列式的计算方法——爪型行列式。(由于公式较多，故正文采用图片形式给出。)

一、爪形行列式简介。

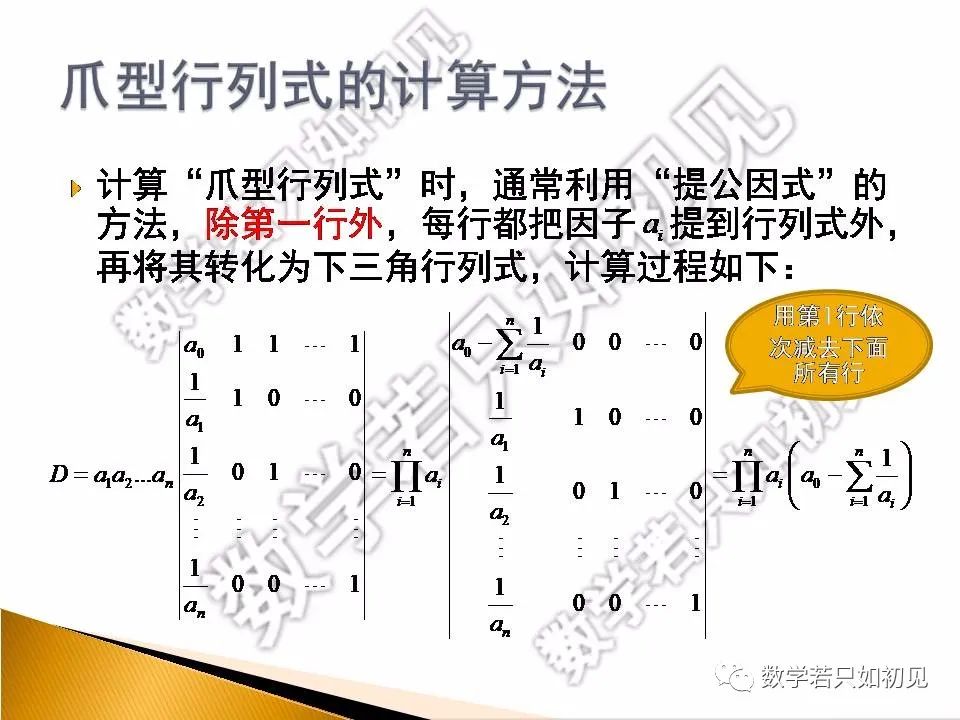
二、爪型行列式的计算方法。(根据行列式的特点，各行提公因子后再化成下三角行列式，另外注意这里计算的D是n+1阶行列式。)

三、转化为“爪型行列式”计算的典型例题。(本例中的行列式不是“爪型”的，但仔细分析元素分布的特点，可以发现各行减去第一行后，就可以化为“爪型”，这种转化的思路在计算行列式问题中是非常普遍的，即将不熟悉的行列式转化为熟悉的形式，例如最常见的化为上三角行列式就属于这种思路。)

四、例题的完整解答(注意计算中一些细节问题的处理)。

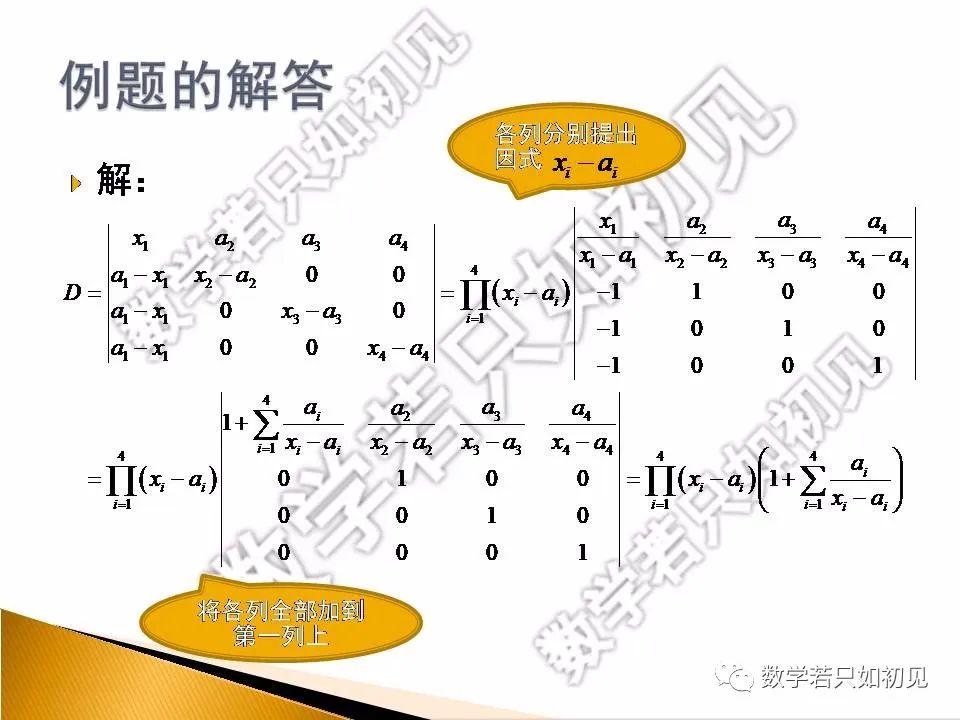
五、对上述解答的一些评注。(对于“爪型行列式”我们要记住的是计算方法而不是计算公式，这一点与以后要介绍的“范德蒙德行列式”不同。)

六、习题。(本题也可不转化为“标准”的爪型行列式，在各行提出公因子后直接采用计算“爪形行列式”的方法来求解，请读者思考。)

上一篇：线性代数入门——一类重要n阶行列式的计算及其应用