点击上方「蓝字」关注我

 写在前面
写在前面前面我们知道了降维分析
学习了PCoA分析
今天学习PCA分析...
PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴,我们发现,大部分方差都包含在前面k个坐标轴中,后面的坐标轴所含的方差几乎为0。于是,我们可以忽略余下的坐标轴,只保留前面k个含有绝大部分方差的坐标轴。事实上,这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,实现对数据特征的降维处理。
思考:我们如何得到这些包含最大差异性的主成分方向呢?
答案:事实上,通过计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值特征向量,选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中,实现数据特征的降维。
PCoA(Principal Co-ordinates Analysis)分析即主坐标分析。它与PCA类似,通过一系列的特征值和特征向量进行排序后,选择主要排在前几位的特征值,找到距离矩阵中最主要的坐标,结果是数据矩阵的一个旋转,它没有改变样本点之间的相互位置关系,只是改变了坐标系统。如何取舍?
在微生物分析中我们会基于beta多样性分析得到的距离矩阵,进行PCA和PCoA分析,具体距离矩阵可见:beta多样性矩阵。PCA是基于样本的相似矩阵(如欧式距离)来寻找主成分,而PCoA是基于相异距离矩阵(欧式距离以外的其他距离,包括binary_jaccard ,bray_curtis ,unweighted_unifrac和weighted_unifrac距离)来寻找主坐标。
在分析的过程中PCA和PCoA分析都会用到降维的思想,但是在降维的过程中必然会造成数据损失,多数情况下,我们在做降维处理的时候,期望维数越低越好,这样我们就可以最大程度地保真原始数据。PCA基于物种丰度矩阵就意味着PCA分析的矩阵维度等于物种数目。同样的道理,PCoA基于样本间的距离矩阵就意味着PCoA分析的矩阵维度与样本数目相关。因此,如果样本数目比较多,而物种数目比较少,那肯定首选PCA;如果样本数目比较少,而物种数目比较多,那肯定首选PCoA。
上期我们已经介绍了PCoA,今天我们主讲PCA。
发表在2019年代的Microbome (IF>10.0)上的一篇文章Comparative metagenomic and metatranscriptomic analyses reveal the breed effect on the rumen microbiome and its associations with feed efficiency in beef cattle,利用宏基因组和宏转录组的关联分析揭示不同牛品种对瘤胃微生物菌群结构及饲料利用率的影响。作者在分析品种对瘤胃细菌(属水平)和古菌(种)的影响时候,做了一个PCoA分析,结果如下图:
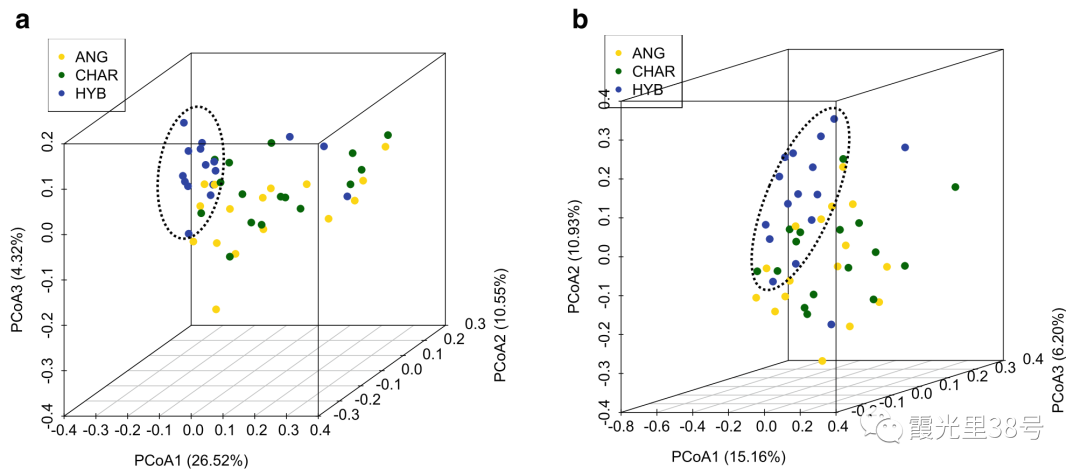
但是如果我们不是分析微生物多样性数据,而是分析其他环境变量,能不能同样做出此图呢?当然可以,但是我们用到的吧不是PCoA,而是PCA分析了。话不多说,我们开始实战。

逐准备数据
在Excel里面输入我们的数据,行为组,检测变量为列,切记一定要遵循此规则,不然后面会出现bug。
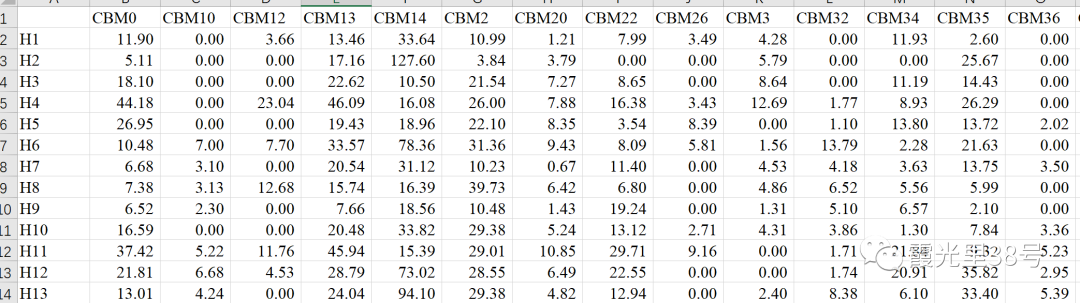

加载包计算PC1
、PC2以及PC3
library(openxlsx)mydatalibrary(vegan)#PCA主要功能包把mydata转化为矩阵,注意第一列为字符,我们要排除第一列
A
Acolnames(A) rownames(A) rownames(A)library(vegan)env##PCA 排序#环境变量需要标准化,详情 ?rdapca_env #I 型标尺summary(pca_env, scaling = 1)#II 型标尺#summary(pca_env, scaling = 2)#各主成分(PCA轴)特征根,特征根是固定的,和标尺选择无关pca_eig #除以特征根总和,即可得各主成分(PCA轴)解释量pca_exp 以上就是我们后面作图要用到的PC1、PC2以及PC3
以上就是我们后面作图要用到的PC1、PC2以及PC3
计算坐标尺度
#提取对象排序坐标,以 I 型标尺为例,以前两轴为例#scores() 提取样方坐标site.scaling1 #或者在 summary 中提取site.scaling1 site.scaling1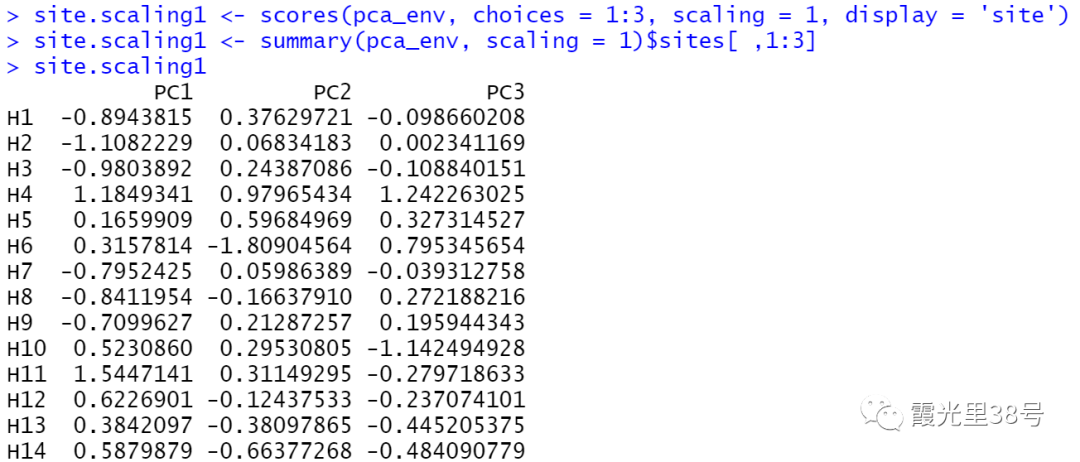 #write.table(site.scaling1, 'site.scaling1.txt', col.names = NA, sep = '\t', quote = FALSE)
#write.table(site.scaling1, 'site.scaling1.txt', col.names = NA, sep = '\t', quote = FALSE)提取变量排序坐标,以 II 型标尺为例,以前两轴为例
#scores() 提取环境变量坐标
env.scaling2
#或者 summary 中提取
env.scaling2
env.scaling2
#write.table(env.scaling2, 'env.scaling2.txt', col.names = NA, sep = '\t', quote = FALSE)
以上就是计算标尺坐标
ggplot2作图
我们用Excel打开输出的pca_site.txt文件。加入我们的组别信息:我们共有三组(group1所示),个数如group2所示:
pca_site
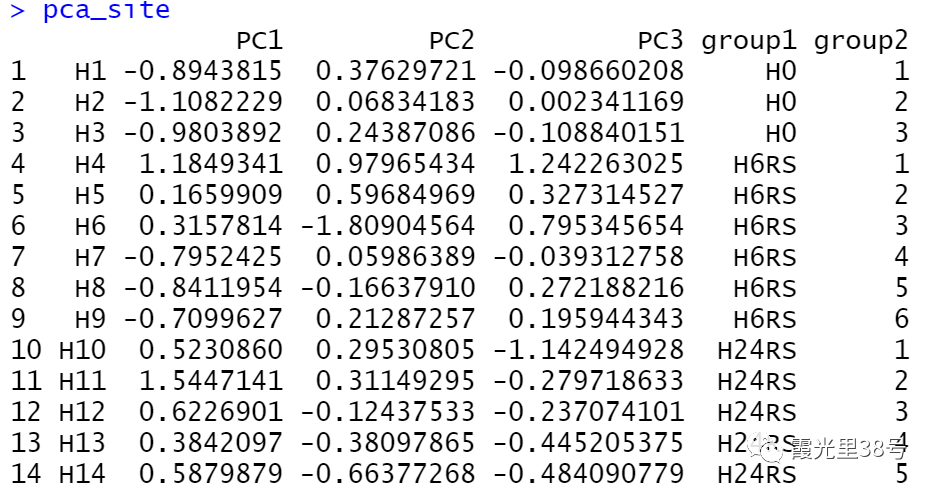
library(scatterplot3d)#加载包
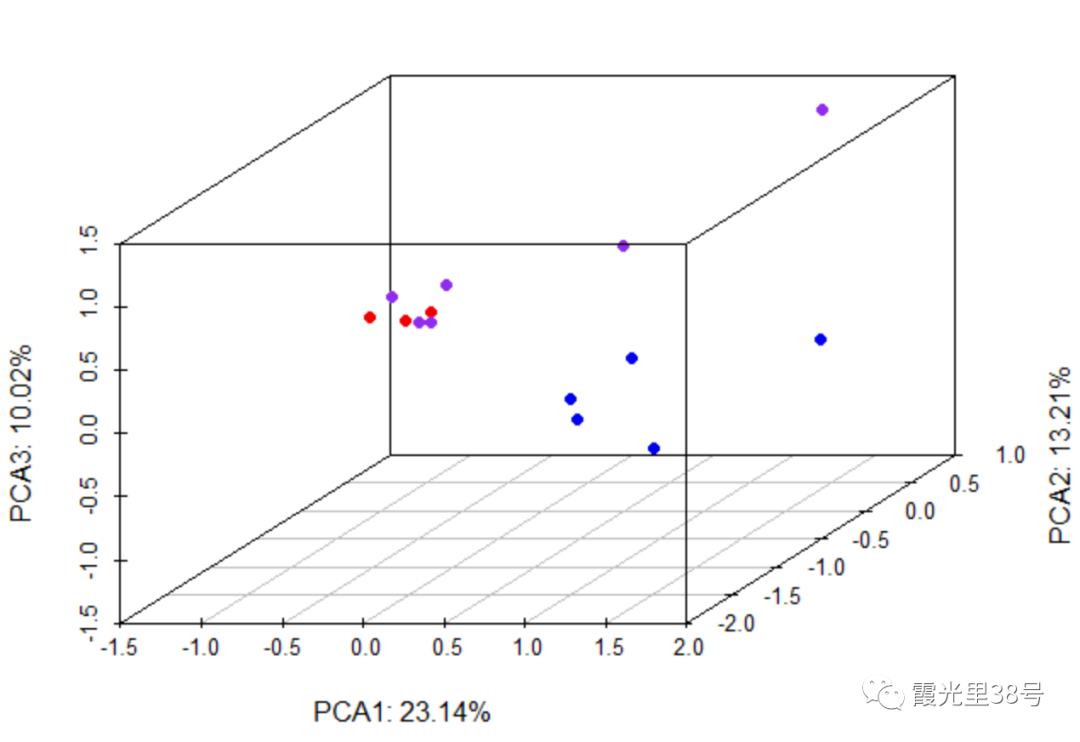
scatterplot3d(pca_site$PC1, pca_site$PC2, pca_site$PC3, pch=16,color = rep(c('red2', 'purple2','blue2'), c(3,6,5)),xlab = paste('PCA1: 23.14%'), ylab = paste('PCA2: 13.21%'), zlab = paste('PCA3: 10.02%'))
c(3,6,5)为样本数量,其中样本数量必须与颜色一致
 是不是很简单易操作,还在犹豫什么赶紧动动手操作吧!
是不是很简单易操作,还在犹豫什么赶紧动动手操作吧!
快开学啦
点赞关注我