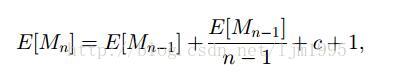阅读此论文主要目的在于理解gossip协议及其背后的原理,此部分详细翻译,其余部分看时间
文章标题:Gossip协议的P2P会员管理
作者:Ayalvadi J. Ganesh, Anne-Marie Kermarrec, and Laurent Massoulie ´
Abstract:基于Gossip的组通信协议具有吸引人的可扩展性和可靠性。迄今为止研究的概率八卦计划通常假定每个团体成员对全球成员有充分的了解,并随机选择八卦目标。全局知识的要求抑制了它对大规模群体的适应性。在本文中,我们提出了SCAMP(可扩展会员协议)——一种新颖的对等会员协议,它以完全分散的方式运行,并为每个成员提供成员的部分视图。我们的协议是自组织的,部分视图的大小可以自然地收敛到可靠支持gossip算法所需要的值。该值是组大小的函数,但是在没有任何节点知道组大小的情况下实现。我们提出了另外的极致来实现平衡的视图大小,即使是在非常不平衡的订阅模式下(也可以达到目的)。我们介绍设计,理论分析和基本协议及其细化的详细评估。模拟结果表明,SCAMP提供的可靠性保证与以往基于全球知识的方案相当。 实验的规模证明了协议的可扩展性。
Introduction:
为了可靠地扩展Internet范围的分布式应用程序组通信,对可扩展机制的需求正在被极大地推动着。网络级可靠的组播协议,如SRM或RMTP依靠IP组播,目前尚未广泛部署。 这激发了对应用级多播协议的需求,目前这是一个积极的研究课题。
基于概率八卦的传播协议正在成为一种具有吸引力的替代方案,它提供了良好的可扩展性和可靠性。在这些协议中,每个成员负责将每个消息转发给一组其他随机选择的组成员。这种主动使用冗余消息的方式提供了一种机制来确保在网络中遇到节点崩溃或高丢包率时候的可靠性。因为每个节点上的负载只能与组的大小呈对数增加,所以这些算法是可扩展的。基于Gossip的协议特别适用于组成员资格相对静态但群组成员的可用性呈间歇性的场景。 由于这些协议容忍高故障率,因此在这种情况下不需要重新配置机制。
虽然这些方法已经被证明是可扩展的消息传播,但是它们依赖于一个不可扩展的成员关系协议:1、它们假设节点gossips(闲话)的节点子集在所有参与节点之间均匀选择,并且要求每个节点应该知道其它每个节点。这对存储器和同步性提出了很高的要求,这会导致其扩展性受到不利影响。在没有任何具有全局会员知识的节点情况下,这有助于分配会员管理的工作,以便为每个节点提供系统的部分随机视图。然而,为了使基于gossip的消息传递成功,每个节点所需的部分成员关系的大小与系统的大小有关。当组增大时,每个节点的部分成员关系大小需要相应增加。在早期工作中,我们得出了实现高度可靠性的扇出(八卦目标的数量),并将其作为系统大小的函数。成员管理集中或分散在几个服务器之间时,可以轻松确定参与的数量,并且可以调整扇出来匹配可靠性要求。但是,在完全分散的模式中,每个节点都以系统的不完整视图运行,这就不是直接可以得知的了。以前提出的部分成员方案都需要知道系统大小。
我们提出了一个可扩展的概率成员协议,旨在解决这个问题。这个协议简单、完全分散而且是资配置的。随着参与节点数量的变化,我们展示了分析情况和模拟情形——部分视图的大小自动适应所需的值。这些结果是针对任意订阅模式(subscription patterns)实现的,包括所有订阅针对同一成员的最坏情况。评估结果表明,基于本协议提供的部分视图的八卦与基于被每个节点知道的全局成员的随机选择的八卦一样,对故障具有弹性。我们提出的协议具有并入现有的基于gossip的方案的潜力,能减少由于成员管理引起的内存和同步开销。
本文的其余部分组织如下:我们在第2节中描述会员协议以及其背后理论的概述。第3节提出了两个互补的优化方案,即使在高度不平衡的订阅模式下也能实现视图的大小平衡。详细评估见第4节。相关工作在第5节中描述,我们在第6节中得出结论。
2 DECENTRALIZED MEMBERSHIP PROTOCOL
2.1 支持基于gossip的多播的要求
基于Gossip的协议使用随机化来可靠地传播组中的消息,它们在发布订阅系统(publish-subscribe systems)、分布式数据库、分布式故障检测、分布式资源环境、虚拟同步等环境中被广泛使用。它们提供了在链接受损或者存在失败节点的情况下概率性交付的保证。当配合合适的更高水平的恢复机制时,它们可以为提供确定性担保提供依据。这些协议的几种实现方式在八卦轮(gossip rounds)的长度以及八卦目标的数量和选择方面有所不同。为了清楚起见,我们以简单的八卦方式测试SCAMP,其中每个节点将每个多播消息一次传播到其他节点的随机子集。但是本文提出的机制和结果适用于基于gossip的多播协议的其他实现。
在基于Gossip的协议中,消息传播如下:当节点生成消息时,它将其发送到其他节点的随机子集。当任何节点第一次接收到消息的时候,它都做上述操作。八卦目标的随机选择为随即失败提供了弹性,并实现了分散化操作。我们使每个成员可选择的八卦目标数量足够大,并把它作为组大小的函数的方式引入足够的冗余,这样保证了可靠性。
问题就在于确定这些随机子集的大小,以便将消息以高可能性可靠地传播给所有群组成员。在早期工作中,有以下清晰的结论:存在n个节点,每个节点平均八卦给log(n)+k个其他节点,则每个节点收到消息的概率收敛到e^-e^-k,这个是指给定节点接收到消息的概率,而不是每个节点接收到的概率。我们将这个属性称为强原子性,已将其与传统的原子性属性^2区别开来。在这个传统的原子性属性^2要求要么没有节点收到消息,要么所有节点都收到消息。 在[17]中,我们还得出了成功概率取决于节点和链路的故障率的表达式。
传统的基于gossip的协议依赖于从所有组成员中随机选择的八卦目标,我们把这种方法称为满成员协议。这种协议需要每个节点有整个组的成员关系信息,它在大群组或成员资格频繁变化的组中是不切实际的。 在[17]中,我们提出了一种方案,一组服务器维护全局成员关系列表,并为个体节点提供周期性更新的随机部分视图。 我们在目前工作中的目标是消除对服务器的需求,并制定完全分散的协议,为每个节点提供部分成员资格。 该协议的设计要求包括:
1、可扩展性:每个节点维护的部分视图的大小应随组大小而增长缓慢。
2、 可靠性:每个节点的部分视图应足够大,来保障它的可靠性与依靠完全了解组成员身份传统方案相比也不落下风。
3、分散操作:在维护上述属性的同时,部分视图应更新为成员订阅或取消订阅。 更新应仅使用本地信息进行。 即使没有节点知道系统大小,部分视图大小也会自动缩放到正确的值作为系统大小的函数。
4、隔离恢复:传统八卦方案的一个重要特征是,每当一个节点闲聊多播消息时,它随机选择新的八卦目标。 因此,就算一个节点偶尔会错过一个消息时,它也不太可能被重复地省略。相比之下,如果节点从部分视图中选择长期保持不变的八卦目标,则需要一种从隔离恢复的机制。
2.2 基础的成员管理协议
该协议由节点订阅(连接)和取消订阅(离开)组的机制,节点可以从隔离中检测和恢复。节点的部分视图以完全分散的方式响应不断变化的组成员而演变。
2.2.1 订阅(Subscription)
订阅算法进行如下:
1、联系人:新节点通过向任意成员发送订阅请求来加入组,称其为联系人。 他们开始的部分视图仅包括他们的联系。
2、新订阅:当一个节点收到一个新的订阅请求时,它将新的node-id转发给自己的本地视图的所有成员, 它还创建了c个新订阅的附加副本(c是确定故障容忍的设计参数),并将其转发到其本地视图中随机选择的节点。
3、转发订阅:当节点接收到转发的订阅的时,如果订阅尚未存在其列表中,它将以概率p将新订阅者集成,该概率p取决于视图的大小。如果没有保留新订阅者,则将订阅转发到其本地视图中随机选择的节点。这些转发的订阅由其邻居保存或转发,但是在某些节点保留之前不会被销毁。
4、保留订阅:每个节点维护两个列表:PartialView和InView。节点发送gossip消息给PartView中的节点,从InView的节点接收gossip消息。如果节点i决定保留节点j的订阅,则将节点j的nodeID放在其PartialView中,并且向节点j发送一条消息,告诉它将节点i的nodeID保留在它的InView中。
算法1描述了接收新订阅的节点的伪代码。 算法2描述了接收转发订阅的节点的伪代码。
算法1 订阅管理 在一个联系节点contact上订阅新订阅者
算法2 处理转发的订阅
此协议仅需要处理订阅请求节点处可用的本地消息,它具有如下属性:如果新节点通过向从现有成员随机选择出来的成员发送订阅请求,则系统将自身配置为大小为(c+1)log(n)的部分视图。n是系统中的节点数,c是设计参数。可以发现,一个通知到达每个节点的概率在log(n)处有一个极其尖锐的阈值:小于log(n)的部分视图接近0,在大于log(n)的部分接近1。这个结果适用于没有故障的系统,并且可以容易地扩展到解决链路和节点故障。例如,如果链接以概率α独立于其它链路失败,那么阈值就是(log(n))/(1-α)。维持某些大小为(c+1)log(n)的视图c>0的另一个原因是它使我们能够选择不同的大小为log(n)+k的子集作为不同消息的gossip目标。这保证了链路和节点故障不太可能导致网络的持续分区,并使我们能够使用为传统八卦协议设计的恢复机制。因此,就算我们保持相当小的部分视图,我们仍然可以获得这些协议的许多好处。
我们使保存转发订阅的概率p=1/(1+sizeof(PartialView))有两个目的:首先,我们使得这个概率是当前部分视图的大小的递减函数,我们的目标是在不同的节点上获得更加平衡的视图大小,从而实现围绕平均视图的大小集中的视图大小的分布。第二,假设部分视图大小大致是(c+1)log(n),在一个订阅被保留之前的转发步骤数量大致平均是(c+1)log(n)。我们可以看出正在考虑的随机图具有与log(n)成比例的直径。我们期望概率p的值能使得转发的订阅在被某个节点保存之前遍历图相当大的部分。
我们现在给出订阅协议的平均值分析。
我们将系统建模为随机定向图:节点对应组成员,并且有一条有向弧(x,y),其中y在x的部分视图中(patial view)中。当一个节点发起新订阅时,我们算法的动作是创建一个随机数量的附加有向弧,如下所示:假设组中已经有n个成员,如果新节点订阅了具有外向度为d的节点,则增加d+c+1个弧。新节点具有外向度1,其中列表仅有其订阅的节点组成。接受订阅的节点将订阅节点的节点id的一个副本转发到其每个邻居,并将附加的c份拷贝转发到随机选择的邻居。所有转发的订阅最终将由某个节点保存。
当节点数量已经增加到n时,让E[Mn]表示预期有向弧数目,使得每个节点的平均出度为E[Mn]/n。假设新节点订阅至一个随机选择的成员,我们有
从上面这个式子我们可以看出E[Mn]≈(c+1)nlogn。
2.2.2 取消订阅
上述订阅机制创建连接图。但是,节点故障或未完成的脚本可能导致网络断开连接。网络可能会断开连接的主要原因是单个节点的隔离。当所有节点在其部分视图中包含其标识符失败的时候,节点与图形隔离。为了重新连接这些节点,我们提出了心跳机制。每个节点向在其部分视图中的节点定期发送心跳消息。长时间没有收到心跳消息的节点知道它被隔离了,它会通过其部分视图中的任意节点重新订阅。此外,第三部分提出的图表重新租赁机制也有助于降低长期隔离的可能性。
3 重新平衡图的机制(这个是新介绍的东西,有时间补上,现在先这样)
然后附一篇对我帮助很大的博文,虽然我觉得gossip-based protocols过程描述方面有点出入,但是能帮助我们较好理解基本思想。
http://blog.csdn.net/zhangxinrun/article/details/7087541?locationNum=12