欢迎光临我的专栏《微积分学习之旅》，一起学习，共同提高。
函数是微积分的基础，我们已经学习了直线函数和多项式函数，本篇中我们继续学习幂函数、有理函数和代数函数。
幂函数（Power Functions）
如果一个函数形如
![]()
，其中a是常数，那么我们称之为幂函数。由于a的不同，幂函数会有三种不同的情况，我们分别讨论一下。
（i）
![]()
,
![]()
是一个正整数
图1分别显示了
![]()
中
![]()
的图像（其实它们也可以看成是只有1项的多项式函数），其中的
![]()
（过原点的直线函数）和
![]()
（过原点的抛物线），我们已经很熟悉了。
其实，
![]()
的形状取决于
![]()
是奇数还是偶数。如果
![]()
是偶数，那么
![]()
就是
，而且它的图像与
![]()
抛物线相似。如果
![]()
是奇数，那么
![]()
就是
，而且它的图像与
![]()
的图像相似。从图2中我们还注意到，
![]()
值增加， ![]()
的图像在 ![]()
附近变得更加平坦，而在 ![]()
处变得更为陡峭。（ii）
![]()
,
![]()
是一个正整数
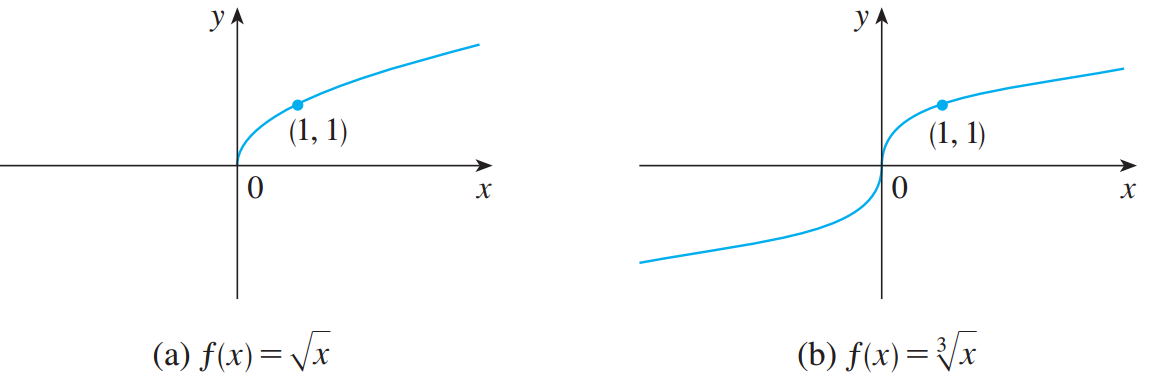
若
![]()
，函数
![]()
是一个
![]()
时，
![]()
称为
，它定义域为
![]()
，其图像为抛物线
![]()
的上半部分。对于其它的偶数值
![]()
，
![]()
的图像与
![]()
的类似。如图3左图所示。
![]()
时，
![]()
称为
，它定义域为
![]()
(因为对于任意实数都有立方根)，其图像 与
![]()
的类似。如图3右图所示。
（iii）
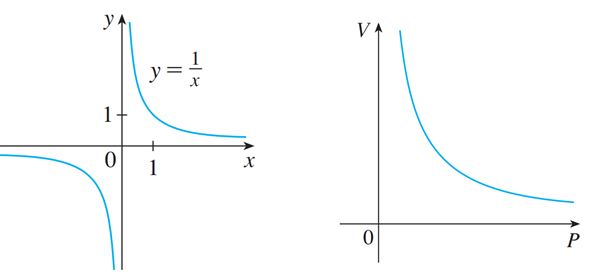
当
![]()
时，函数
![]()
称为
，如图4左图所示，它的图像是以坐标轴为渐近线（asymptotes）的
双曲线（hyperbola）。这个函数的典型例子是物理和化学中的玻意耳定律（Boyle's Law），这个规律认为，当温度恒定时，气体体积
![]()
与气体压强
![]()
成反比。即
![]()
。这里的
![]()
是常数，由于压强和体积均为正数，所以它的图像只有双曲线的一支。
幂函数也常常用于光照强度关于到光源距离的函数，行星公转周期关于到太阳间距离的函数等。
有理函数（Rational Functions）
如果函数
![]()
可以表示为两个多项式的比值，我们就称之为有理函数，即：
这里的
![]()
和
![]()
都是多项式。值得注意的是，有理函数的定义域需要满足
![]()
。最简单的有理函数就是上面提及的倒数函数如
![]()
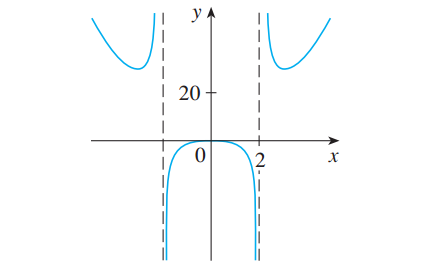
。再比如下方的有理函数，它的定义域为
![]()
,它的图像如图5所示。
代数函数（Algebraic Functions）
如果一个函数
![]()
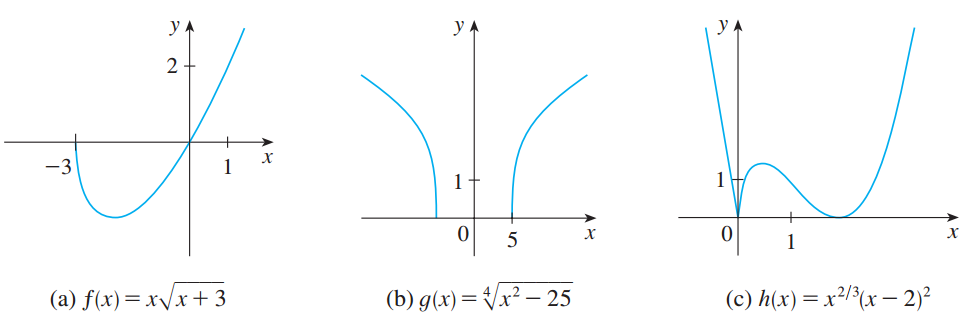
可以由多项式经过代数运算（加、减、乘、除、求根）得到，那么它就是代数函数。显然，任何有理函数天生就是一个代数函数。再来两个例子：
代数函数的图像可以多种多样，没有一定规律，比如下面这样的。
图6代数函数的一个典型例子就是相对论中的质量关于速度的函数：
这里的
![]()
是质点的静止质量（rest mass），
![]()
是真空中的光速。
小结：
本篇主要介绍了幂函数、有理函数、分式函数的定义及其主要特点。在下一篇中，我们还将认识三角函数、指数函数和对数函数。
本专栏目录请参阅：
Mr.Xiong：专栏目录-《微积分学习之旅》zhuanlan.zhihu.com
（如果您喜欢本专栏，请点击关注；如果认可我的笔记，也请点个赞同呗）
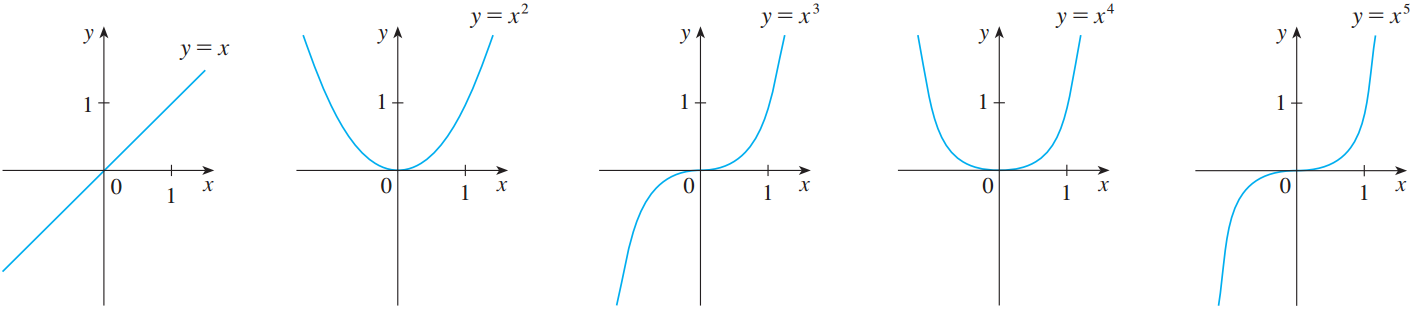
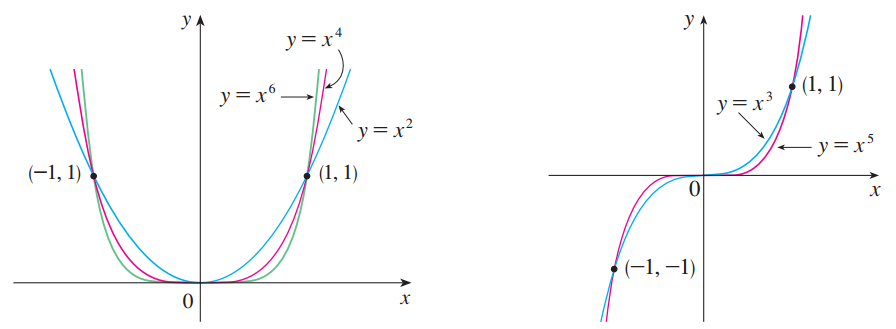
![shell su 密码_[SU模型] 59个公共卫生间](https://img-blog.csdnimg.cn/img_convert/5b23ec0629bb1cde86b678e2bbf956e0.png)
