摘要 用数轴的点表示数, 实际是把数的几何意义单一 化, 把所有实数同等化. 在研究素数的问题上, 应该挖掘数的 更多几何意义, 就正自然数而言, 不同区间的数, 几何意义是 不相同的, 对应的点是不同空间的点, 具有多样化的. 寻找质 数, 就是设法把不同空间的 1 维数 (质数) 找出来. 先通过质 数相乘的办法把合数找出来. 合数找到了, 质数就呈现了. 改 变了传统把数进行质因数分解. 把做除法的工作改为做乘法 的工作.
关键词 质数; 素数; 质因子; 合数; 空间性; 维度性
>>>>
1. 找最大质数仍是世界难题
质数也叫素数, 指在一个大于 1 的自然数中, 只能被自 己和 整除的数. 大于 的自然数, 除了质数就是合数. 按照 规定, 不算素数 (也不是合数), 最小的素数是 , 其后依次是 、 、 、 等等. 素数是无穷多的. 它们的分布距离是不均等的. 目前我们掌握的素数很有限, 因为数字越大, 要发现新的 素数就越困难.
因此, 要找到一个大的素数, 往往需要巨量的计算, 要分 解和验证它也是这样.
“梅森素数”是一种有特殊形式的素数, 写成 的 形式, 寻找梅森素数是目前发现已知最大素数的最有效途径. 这个项目的全称是“互联网梅森素数大搜索”(The Great Internet Mersenne Prime Search, 简称 GIMPS), 它始于 1996 年, 由世界各地的志愿者自愿花时间计算梅森素数. 他们从 GIMPS 网站上下载免费软件, 当计算机闲置时, 这个软件就 开始在数轴上进行梳理式计算. 在已知的梅森素数中, 有不 少就是通过这个渠道找到的.
2017 年 12 月 26 日, 互联网梅森素数大搜索 (GIMPS) 项 目 宣 布 发 现 第 50 个 梅 森 素 数 和 已 知 最 大 的 素 数: , 共有 , , 位. 发现者是 GIMPS 志愿 者 Jonathan Pace, 是一位电机工程师.
2018 年 12 月 7 日, 住在美国佛罗里达州奥卡拉市的 Patrick Laroche 也是通过 GIMPS 项目发现了第 个梅森素 数: (被称为 ), 共有 , , 位 [1] .
为了研究素数, 数学家呕心沥血, 从未止步.
对于寻找更大的素数问题, 我经历了长期的探索, 发现 新方法 (分段追寻法): 先赋予 (或说发掘) 数字的空间和维度,
把数字按空间分类 (或说分段), 然后从已知的质数出发, 找 出合数, 排除合数, 得出更大的质数.
2. 数字的空间性
用数轴的点表示数, 实际是把数的几何意义单一化, 把 所有实数同等化. 在研究素数的问题上, 应该挖掘数的更多 几何意义, 就正自然数而言, 不同区间的数, 几何意义是不相 同的, 对应的点是不同空间的点, 具有多样化的 [2] .
我们把某些正自然数图形化 (如下表), 从而理解数字的 几何意义.
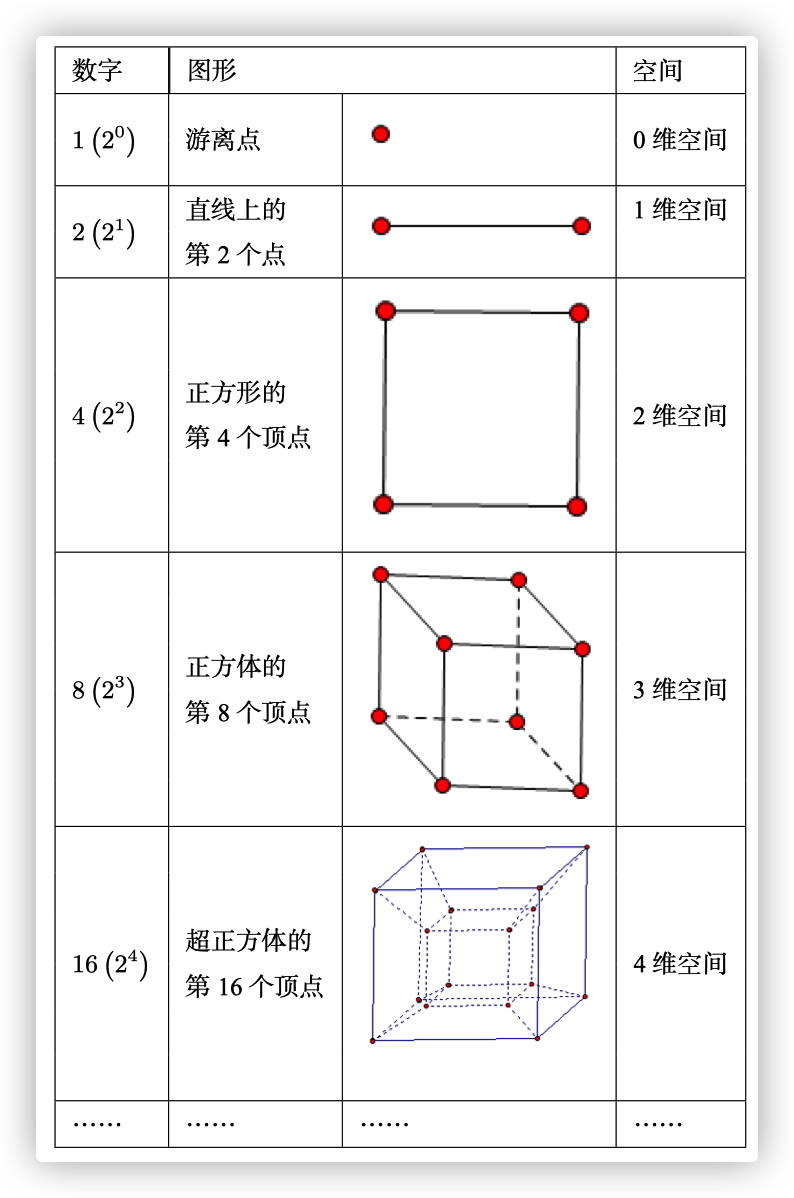
从数的几何意义, 我赋予 (或说发现) 数字的空间性:

3. 数字的维度性
我们知道, 每个合数都可以写成几个质数相乘的形 式, 其中每个质数都是这个合数的因数, 叫做这个合数 的分解质因数. 每个合数能够且仅能够被分解为唯一一 组质因数的乘积. 根据这原理, 我们可以赋予 (或说发现) 数字的维度: , , , ……所有质数的维 度是 ; , , , …… , , 的维度是 ; , …… 和 的维度是 . 总之, 一个合 数的所有质因数的次数之和就是该合数的维度, 合数的维度 最小为 , 质数的维数是 , 既不是质数也不是合数, 维度为 .
4. 质数的分段追寻
根据数字的空间性, 我把自然数进行分类和分段:
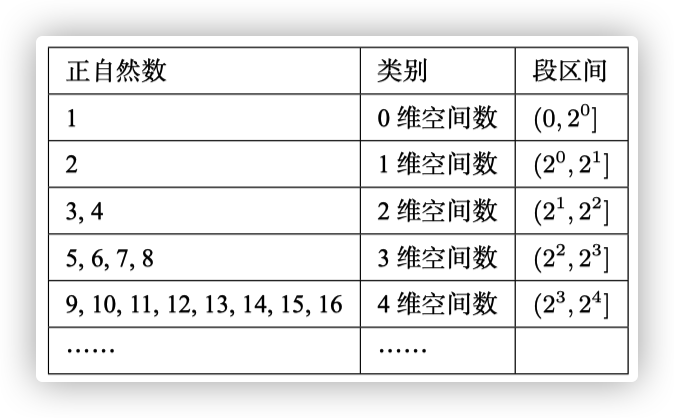
依上表呈现的类别, 逐段进行质数的追寻. 下面, 以 维 空间数和 维空间数这两段为例, 说明追寻的方法.
例 1 已知: 和 维空间数的质数是 ,
求: 维空间数的质数个数.
解: 第一步, 确定三维空间数段区间端点 , ;
第二步, 确定三维空间数 , , ,
第三步, 确定三维空间数中的二维数 (合数), 质因子依 次从小到大列举, , 共 个 , 是 .
确定三维空间数中的三维数 (合数), , 即右端点, 共 个, 是 .
第四步, 确定三维空间数中质数的个数: . 其中, 是三维空间数的个数, 是第三步确定的合数个数. 完毕.
例 2 已知: 至 维空间数的质数是
求: 维空间数的质数
解: 第一步, 确定四维空间数段区间端点 ;
第二步, 确定四维空间数
第三步, 确定四维空间数中的二维数 (合数), 质因子依 次从小到大列举, 共 个, 分别是 .
确定四维空间数中的三维数 (合数), 质因子依次从小到 大列举, 共 个, 是 .
确定四维空间数中的四维数 (合数), , 即右端点, 共 个, 是 .
第四步,确定四维空间数中质数的个数: . 其中, 是四维空间数的个数, 是第三步确定的合数个数.
第五步, 通过比较四维空间数 和第三步找出的合数 . 确定三维空间数中的 质数是 和 . 完毕.
同理, 我们可以用例 1 和例 2 的方法解决下面的问题.
已知: 在区间 的质数有
求: 在区间 的质数
5. 世界难题的突破
上述的方法实际是把不同空间的 维数 (质数) 找出来. 先通过质数相乘的办法把合数确定, 排除了合数, 就是质数. 改变了传统的把数进行质因数分解. 把做除法的工作改为做 乘法的工作.
把数字空间化, 实现了自然数的合理分类 (分段). 数字 维度化, 确保了列举合数时不重复. 按质因子依次从小到大 顺序列举, 确保了合数不遗漏. 只要计算机给予足够的运算 支持, 下面的世界难题就得以突破.
已 知: 在 区 间 的 质 数 有 .
求: 在区间 的质数
解 决 了 这 一 问 题 后, 同 理, 可 以 求 下 一 段 的质数. 这样, 我们就可以求出更多 更大的质数, 没有最大, 只有更大.
参考文献
[1] 百度百科
[2] 张煜明. 由螺旋型计数得出的一系列数列, 中学数学研究 [M], 2015, 2:45-46
作者:张煜明,中学数学高级教师,1996年毕业于华南师范大学数学系
—版权声明—
来源:《中学数学研究》,编辑:nhyilin
仅用于学术分享,版权属于原作者。
若有侵权,请联系微信号:Eternalhui或nhyilin删除或修改!
—THE END—
文章推荐
☞完美数:数学宝库中的一颗璀璨明珠
☞15岁进少年班,21岁打破西方技术壁垒!这位95后正在改变世界
☞名校博士被撤销学位,只因7行文字抄袭及1张互联网图片……
☞我见过最糟糕的代码
☞数论大牛John Coates:如果我建数学系,将采用剑桥模式
☞央行这篇工作论文火了!房价太高“逼走年轻人”,中等收入陷阱“文科生太多”…

...)


















_学小易找答案)