刚体运动学
刚体模型
刚体是一个特殊的质点系, 刚体上任意两质点间距离保持不变。
刚体模型可以看成是现实中劲度系数极大的物体的抽象化,这类物体本身的形变对其运动的影响可以忽略,比如一个篮球,当其与地面碰撞时必然会产生形变,但这个形变对其运动的印象是微乎其微的(有些人认为,如果忽略形变,那么弹力怎么解释?我个人对刚体模型的理解是,刚体虽然忽略了形变,但是保留了由形变而产生的弹力), 我们完全可以将其抽象成一个具有一定质量分布的刚体球,考察它在与地面时,地面摩擦力和弹力对它的影响。
刚体模型具有两个显然的性质:
(1)刚体上任意两点的速度沿两点连线方向的分量相等
(2)刚体内任意两质点间的一对相互作用力做功始终为零
刚体的平动与转动,刚体运动的自由度
平动:保持了刚体上任意两点间的连线矢量方向不变的运动。刚体平动的特征是,刚体上任意两点的速度始终相同,加速度始终相同,因此在描述刚体平动时只需选择刚体上的一点即可,通常我们选择质心作为描述对象。
转动:围绕刚体上某一点(轴)的旋转运动。刚体的转动可以分为定点转动(绕一点)和定轴转动(绕一轴)。
刚体任意运动可以被分解为刚体的一次平动与绕某一点的转动的叠加。
完全自由的刚体拥有六个自由度:三个平动自由度和三个转动自由度。
刚体的定轴转动
刚体围绕空间中一个固定轴转动的运动叫做刚体的定轴转动,定轴转动只有一个自由度,可以用一个参量角速度
刚体的平面运动
刚体上任一点的运动都限制在同一平面上的运动称为刚体的平面运动,显然此时所有的平面都平行,我们只需要研究刚体在某一平面上投影的运动即可,该被选定的平面被称为“基面”,选定基面上一个随刚体运动的点为“基点”,于是刚体的平面运动可以分解为基点的平面运动与刚体绕基点的转动,故刚体的平面运动具有三个自由度。穿过基点与基面垂直的轴为“基轴”。刚体的平面运动可以由基点速度
刚体角速度矢量的唯一性
刚体在任意运动中的任意时刻具有唯一的角速度矢量,这个角速度矢量会随刚体的运动而变化,但在任意时刻,始终唯一确定,角速度矢量是属于刚体整体的物理量,源自于刚体本身的性质。
定轴转动惯量
刚体的定轴转动惯量
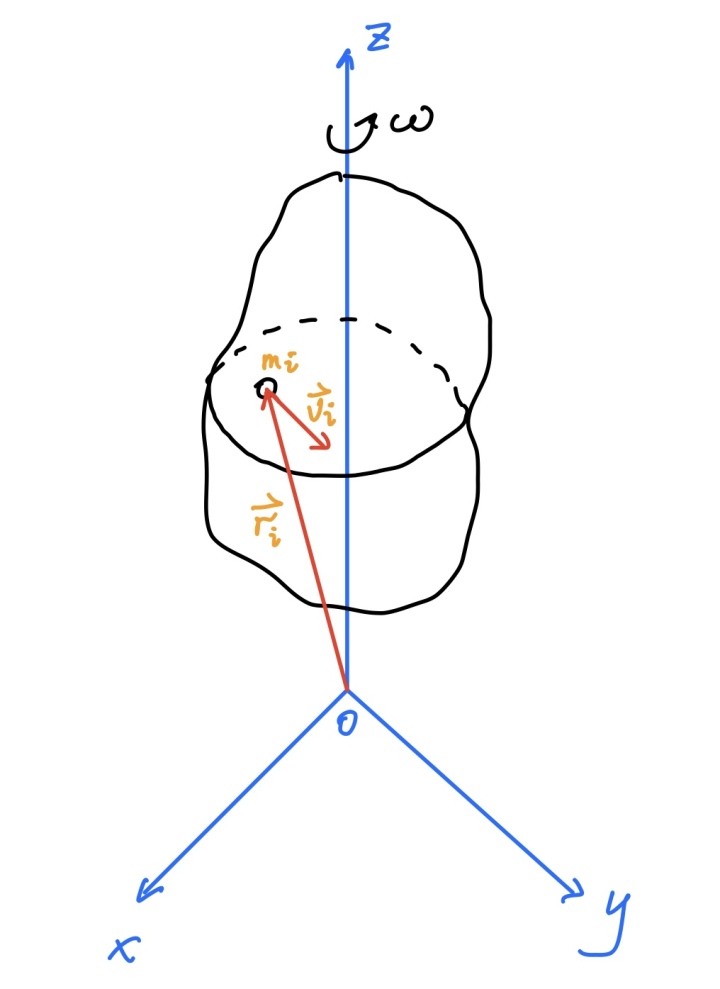
如图所示,刚体绕z轴以角速度
得到角动量沿三个轴的分量,
定义:定轴转动惯量,
于是刚体绕z轴的角动量可以表示为
定轴转动惯量的计算公式
对于由离散质点系构成的刚体,
对于具有质量线分布的刚体,
对于具有质量面分布的刚体,
对于具有质量体分布的刚体,
常见刚体模型的转动惯量
匀质圆盘绕中心轴的转动惯量:
匀质球壳绕某一直径的转动惯量:
匀质球体绕某一直径的转动惯量:
关于定轴转动惯量的两个定理
(1)平行轴定理
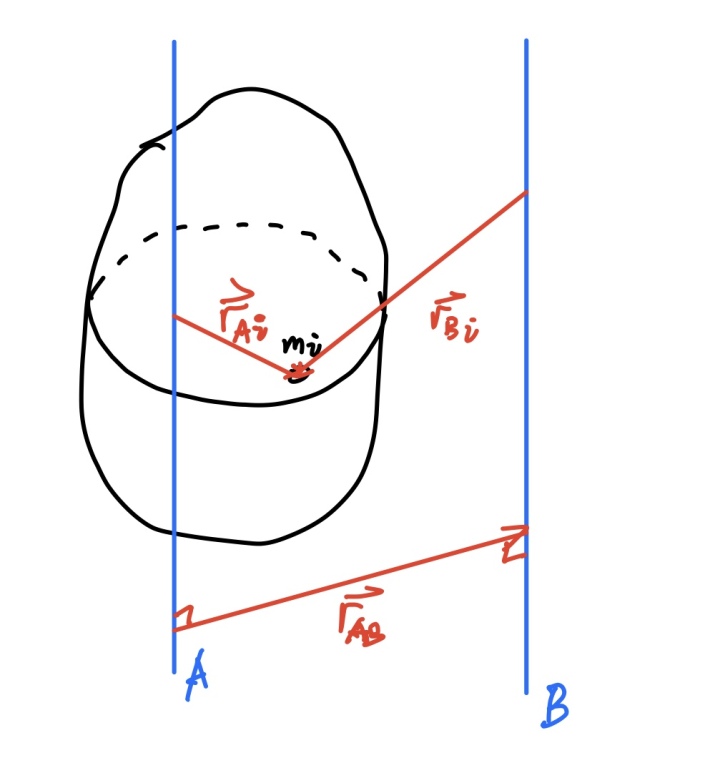
平行轴定理:刚体绕与质心轴平行的转轴的转动惯量等于刚体绕质心的转动惯量和质心绕该轴的转动惯量的和,可以表示为
推导:
当A轴穿过刚体质心时,求和式结果为零,故第三项为零,从而平行轴定理得证。
(2)垂直轴定理
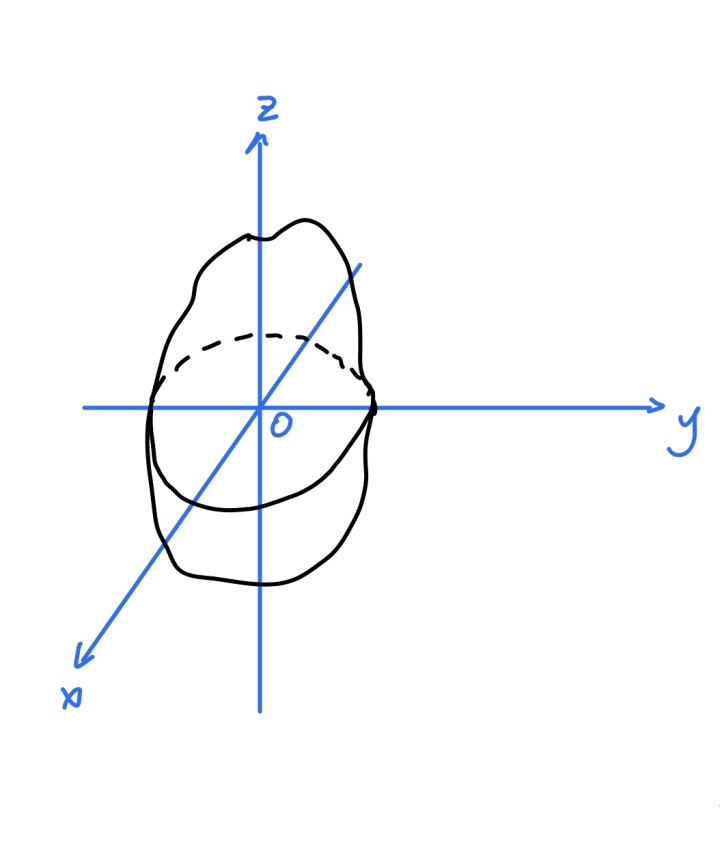
垂直轴定理:刚体绕三条互相垂直的轴的转动惯量之和
特别的,对于薄板而言,我们有薄板的垂直轴定理:假设x,y轴在薄板面内,z轴垂直于薄板面,则有
刚体定轴转动的动力学
定轴转动定理
刚体的定轴转动定理实际上是第五讲中质点系的角动量定理的特殊化,后者指出,质点系的角动量变化量等于质点系所受外力的冲量矩,做变形易得,刚体定轴转动角加速度与转动惯量的乘积等于刚体所受的绕转轴的力矩,表示为,
同时我们可以知道刚体定轴转动角动量守恒条件,
定轴转动的动能定理
刚体定轴转动的动能表示为,
从而可以得到定轴转动动能定理,
刚体平面运动的动能
之前讲到刚体平面运动任一点的速度
小结
本讲引入了刚体这一力学模型,介绍了刚体运动学基本知识,随后介绍了刚体绕轴的转动惯量这一重要物理量以及其相关定理,最后介绍了刚体定轴转动的动力学定理。
在文章最后推荐一个回答
大学物理第六章刚体问题基本的解题思路有哪些?www.zhihu.com









)



 | 学步园)





