Rosenbrock函数的定义如下：

其函数图像如下：

我分别使用梯度下降法和牛顿法做了寻找Rosenbrock函数的实验。

梯度下降

梯度下降的更新公式：

图中蓝色的点为起点，橙色的曲线(实际上是折线)是寻找最小值点的轨迹，终点(最小值点)为 (1,1)(1,1)。

梯度下降用了约5000次才找到最小值点。

我选择的迭代步长 α=0.002α=0.002，αα 没有办法取的太大，当为0.003时就会发生振荡：

牛顿法

牛顿法的更新公式：

Hessian矩阵中的每一个二阶偏导我是用手算算出来的。

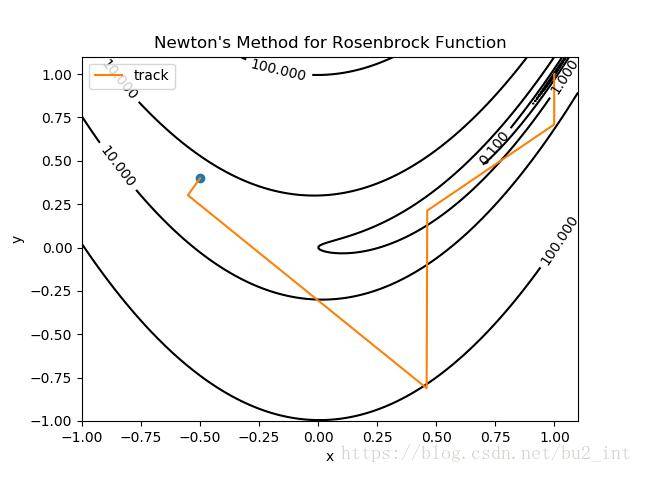
牛顿法只迭代了约5次就找到了函数的最小值点。

下面贴出两个实验的代码。

梯度下降：

import numpy as np

import matplotlib.pyplot as plt

from matplotlib import ticker

def f(x, y):

return (1 - x) ** 2 + 100 * (y - x * x) ** 2

def H(x, y):

return np.matrix([[1200 * x * x - 400 * y + 2, -400 * x],

[-400 * x, 200]])

def grad(x, y):

return np.matrix([[2 * x - 2 + 400 * x * (x * x - y)],

[200 * (y - x * x)]])

def delta_grad(x, y):

g = grad(x, y)

alpha = 0.002

delta = alpha * g

return delta

# ----- 绘制等高线 -----

# 数据数目

n = 256

# 定义x, y

x = np.linspace(-1, 1.1, n)

y = np.linspace(-0.1, 1.1, n)

# 生成网格数据

X, Y = np.meshgrid(x, y)

plt.figure()

# 填充等高线的颜色, 8是等高线分为几部分

plt.contourf(X, Y, f(X, Y), 5, alpha=0, cmap=plt.cm.hot)

# 绘制等高线

C = plt.contour(X, Y, f(X, Y), 8, locator=ticker.LogLocator(), colors='black', linewidth=0.01)

# 绘制等高线数据

plt.clabel(C, inline=True, fontsize=10)

# ---------------------

x = np.matrix([[-0.2],

[0.4]])

tol = 0.00001

xv = [x[0, 0]]

yv = [x[1, 0]]

plt.plot(x[0, 0], x[1, 0], marker='o')

for t in range(6000):

delta = delta_grad(x[0, 0], x[1, 0])

if abs(delta[0, 0]) < tol and abs(delta[1, 0]) < tol:

break

x = x - delta

xv.append(x[0, 0])

yv.append(x[1, 0])

plt.plot(xv, yv, label='track')

# plt.plot(xv, yv, label='track', marker='o')

plt.xlabel('x')

plt.ylabel('y')

plt.title('Gradient for Rosenbrock Function')

plt.legend()

plt.show()

牛顿法：

import numpy as np

import matplotlib.pyplot as plt

from matplotlib import ticker

def f(x, y):

return (1 - x) ** 2 + 100 * (y - x * x) ** 2

def H(x, y):

return np.matrix([[1200 * x * x - 400 * y + 2, -400 * x],

[-400 * x, 200]])

def grad(x, y):

return np.matrix([[2 * x - 2 + 400 * x * (x * x - y)],

[200 * (y - x * x)]])

def delta_newton(x, y):

alpha = 1.0

delta = alpha * H(x, y).I * grad(x, y)

return delta

# ----- 绘制等高线 -----

# 数据数目

n = 256

# 定义x, y

x = np.linspace(-1, 1.1, n)

y = np.linspace(-1, 1.1, n)

# 生成网格数据

X, Y = np.meshgrid(x, y)

plt.figure()

# 填充等高线的颜色, 8是等高线分为几部分

plt.contourf(X, Y, f(X, Y), 5, alpha=0, cmap=plt.cm.hot)

# 绘制等高线

C = plt.contour(X, Y, f(X, Y), 8, locator=ticker.LogLocator(), colors='black', linewidth=0.01)

# 绘制等高线数据

plt.clabel(C, inline=True, fontsize=10)

# ---------------------

x = np.matrix([[-0.3],

[0.4]])

tol = 0.00001

xv = [x[0, 0]]

yv = [x[1, 0]]

plt.plot(x[0, 0], x[1, 0], marker='o')

for t in range(100):

delta = delta_newton(x[0, 0], x[1, 0])

if abs(delta[0, 0]) < tol and abs(delta[1, 0]) < tol:

break

x = x - delta

xv.append(x[0, 0])

yv.append(x[1, 0])

plt.plot(xv, yv, label='track')

# plt.plot(xv, yv, label='track', marker='o')

plt.xlabel('x')

plt.ylabel('y')

plt.title('Newton\'s Method for Rosenbrock Function')

plt.legend()

plt.show()

以上这篇python使用梯度下降和牛顿法寻找Rosenbrock函数最小值实例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持。