模型拟合一般来说有这么三种：
- 切比雪夫近似准则
- 极小化绝对偏差之和
- 最小二乘准则
这几个原则各有各的适用范围。其中最小二乘准则是比较容易计算的。接下来我将简要的介绍最小二乘准则以及举例说明如何用python实现。
最小二乘准则
定义：给定某种函数类型
拟合直线
如果我们要拟合的是直线，即
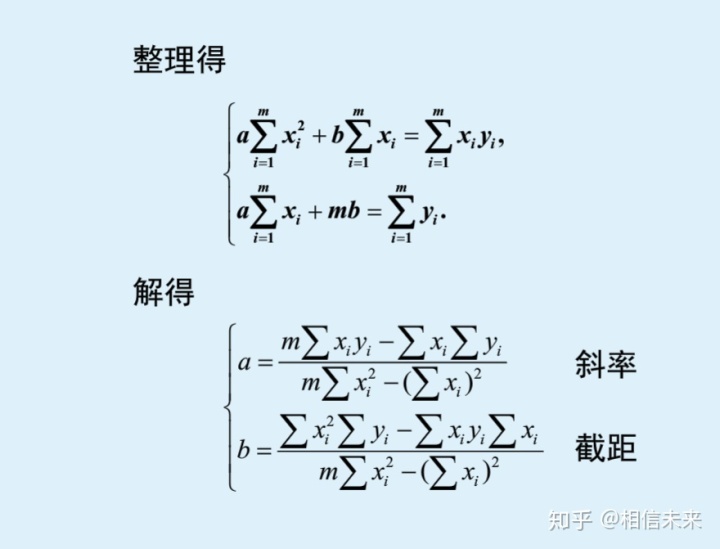
拟合幂函数
可化为线性拟合的非线性拟合
用python求解
我们发现如果要自己计算的话，要用到偏导数，无穷级数的知识。如果数据点很多的话，函数比较复杂的，计算是十分困难的，甚至是不可能的。于是想到可以使用计算机求解。
通用代码如下：
# -*- coding: utf-8 -*-
举例
接着我用我的一篇文章中车辆停止举例为例进行拟合，相关数据在该文章里。
相信未来：从简单数学建模开始：05如何进行数学建模——以车辆停止距离模型为例zhuanlan.zhihu.com子模型一：反应距离模型
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
%pylab inline
plt.rcParams['font.sans-serif']=['simhei']
plt.rcParams['axes.unicode_minus']=Falsedr = np.array([22,28,33,39,44,50,55,61,66,72,77,83,88])
v = np.array([20., 25., 30., 35., 40., 45., 50., 55., 60., 65., 70., 75., 80.])
db = np.array([20,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376])
d = np.array([42,56,73.5,91.5,116,142.5,173,209.5,248,292.5,343,401,464])x = v
y = drdef func(p):k = preturn y - k*xr = leastsq(func,[np.sum(dr)/np.sum(v)])
k = r[0]
print('k=',k)plt.scatter(x,k*x,label = '拟合解')
plt.plot(x,k*x)
plt.scatter(x,y,label='观测解')
plt.plot(x,y)
plt.xlabel('dr')
plt.ylabel('v')
plt.title('最小二乘法则应用')
plt.legend()
plt.show()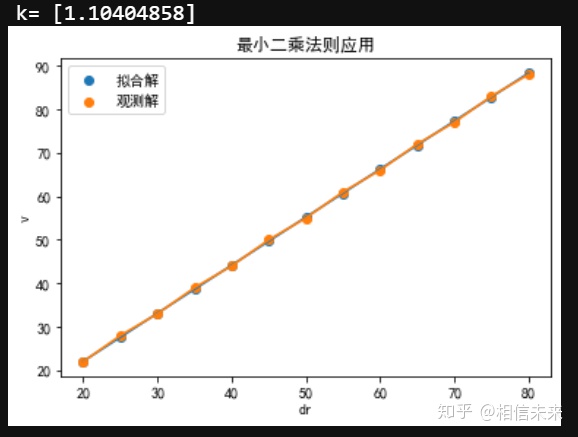
这是拟合后的结果，k = 1.1040，之前的结果为k = 1.1016
子模型二：刹车距离模型
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
%pylab inline
plt.rcParams['font.sans-serif']=['simhei']
plt.rcParams['axes.unicode_minus']=Falsedr = np.array([22,28,33,39,44,50,55,61,66,72,77,83,88])
v = np.array([20., 25., 30., 35., 40., 45., 50., 55., 60., 65., 70., 75., 80.])
db = np.array([20,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376])
d = np.array([42,56,73.5,91.5,116,142.5,173,209.5,248,292.5,343,401,464])x = v**2
y = dbdef func(p):k = preturn y - k*xr = leastsq(func,[np.sum(db)/np.sum(v**2)])
k = r[0]
print('k=',k)plt.scatter(x,k*x,label = '拟合解')
plt.plot(x,k*x)
plt.scatter(x,y,label='观测解')
plt.plot(x,y)
plt.xlabel('dr')
plt.ylabel('v')
plt.title('最小二乘法则应用')
plt.legend()
plt.show()
这张图拟合前和拟合后的差距还是挺大的。
