区域分割一般认为有漫水填充，区域分裂与合并，分水岭，这篇是中间的区域分裂和合并。

区域分裂合并算法的基本思想是先确定一个分裂合并的准则,即区域特征一致性的测度,当图像中某个区域的特征不一致时就将该区域分裂成4个相等的子区域,当相邻的子区域满足一致性特征时则将它们合成一个大区域,直至所有区域不再满足分裂合并的条件为止.当分裂到不能再分的情况时，分裂结束，然后它将查找相邻区域有没有相似的特征，如果有就将相似区域进行合并，最后达到分割的作用。在一定程度上区域生长和区域分裂合并算法有异曲同工之妙，互相促进相辅相成的，区域分裂到极致就是分割成单一像素点，然后按照一定的测量准则进行合并，在一定程度上可以认为是单一像素点的区域生长方法。区域生长比区域分裂合并的方法节省了分裂的过程，而区域分裂合并的方法可以在较大的一个相似区域基础上再进行相似合并，而区域生长只能从单一像素点出发进行生长(合并)。

反复进行拆分和聚合以满足限制条件的算法。

令R表示整幅图像区域并选择一个谓词P。对R进行分割的一种方法是反复将分割得到的结果图像再次分为四个区域，直到对任何区域Ri，有P(Ri)=TRUE。这里是从整幅图像开始。如果P(R)=FALSE，就将图像分割为4个区域。对任何区域如果P的值是FALSE．就将这4个区域的每个区域再次分别分为4个区域，如此不断继续下去。这种特殊的分割技术用所谓的四叉树形式表示最为方便(就是说，每个非叶子节点正好有4个子树)，这正如图10.42中说明的树那样。注意，树的根对应于整幅图像，每个节点对应于划分的子部分。此时，只有R4进行了进一步的再细分。

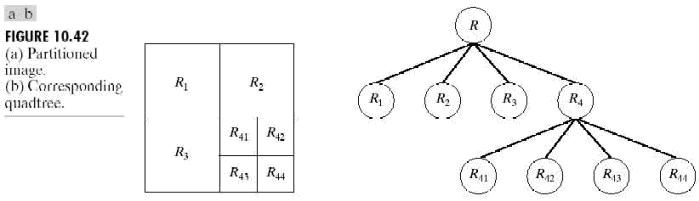
如果只使用拆分，最后的分区可能会包含具有相同性质的相邻区域。这种缺陷可以通过进行拆分的同时也允许进行区域聚合来得到矫正。就是说，只有在P(Rj∪Rk)=TRUE时，两个相邻的区域Rj和Rk才能聚合。

前面的讨论可以总结为如下过程。在反复操作的每一步，我们需要做：

l.对于任何区域Ri，如果P(Ri)=FALSE，就将每个区域都拆分为4个相连的象限区域。

2.将P(Rj∪Rk)=TRUE的任意两个相邻区域Rj和Rk进行聚合。

3.当再无法进行聚合或拆分时操作停止。

可以对前面讲述的基本思想进行几种变化。例如，一种可能的变化是开始时将图像拆分为一组图象块。然后对每个块进一步进行上述拆分，但聚合操作开始时受只能将4个块并为一组的限制。这4个块是四叉树表示法中节点的后代且都满足谓词P。当不能再进行此类聚合时，这个过程终止于满足步骤2的最后的区域聚合。在这种情况下，聚合的区域可能会大小不同。这种方法的主要优点是对于拆分和聚合都使用同样的四叉树，直到聚合的最后一步。

例10.17拆分和聚合

图10.43(a)显示了一幅简单的图像。如果在区域Ri内至少有80％的像素具有zj-mi≤2σi的性质，就定义P(Ri)=TRUE，这里zj是Ri内第j个像素的灰度级，mi是区域Ri的灰度级均值，σi是区域Ri内的灰度级的标准差。如果在此条件下，P(Ri)=TRUE，则设置Ri内的所有像素的值等于mi。拆分和聚合使用前速算法的要点完成。将这种技术应用于图10.43(a)所得结果示于图10.43(b)。请注意，图像分割效果相当好。示于图10.43(c)中的图像是通过对图10.43(a)进行门限处理得到的，门限值选在直方图中两个主要的尖峰之间的中点。经过门限处理，图像中生成的阴影(和叶子的茎)被错误地消除了。

如前面的例子中所使用的属性那样，我们试图使用基于区域中像素的均值和标准差的某些特性对区域的纹理进行量化(见11.3.3节中关于纹理的讨论)。纹理分割的概念是以在谓词P(Ri)中使用有关纹理的量度为基础的。就是说，通过指定基于纹理内容的谓词，我们可以使用本节中讨论的任何方法进行纹理分割。

1. 把一幅图像分成4份，计算每一份图像的最大灰度值与最小灰度值的差， 如果差在误差范围值外，则该份图像继续分裂。

2. 对于那些不需要分裂的那些份图像可以对其进行阈值切割了，例如某一块图像的最大灰度大于某个值，则该块图像变成255，否则变为0。

// 代码

// 区域分裂合并的图像分割

// nOffSetLne是行偏移量

// 由于分裂的层数太多了, 使用递归将使内存空间堆栈溢出

// 解决方法是使用一个堆栈对要分裂的块入栈

// 使用堆栈的方法类似在"区域生长"的实现方法

#include

struct SplitStruct

{

unsigned int nWidth; // 这一块图像的宽度

unsigned int nHeigh; // 这一块图像的高度

unsigned int nOffSetWidth; // 相对源图像数据的偏移宽度

unsigned int nOffSetHeigh; // 相对源图像数据的偏移高度

};

void AreaSplitCombineEx(BYTE* image0, // 源图像数据

unsigned int nAllWidth, // 源图像的宽度

unsigned int nAllHeigh, // 源图像的高度

unsigned int w, // 这一块图像的宽度

unsigned int h, // 这一块图像的高度

unsigned int nOffSetWidth, // 相对源图像数据的偏移宽度

unsigned int nOffSetHeigh) // 相对源图像数据的偏移高度

{

std::stack nMyStack;

SplitStruct splitStruct, splitStructTemp;

splitStruct.nWidth = w;

splitStruct.nHeigh = h;

splitStruct.nOffSetWidth = nOffSetWidth;

splitStruct.nOffSetHeigh = nOffSetHeigh;

nMyStack.push(splitStruct);

int i, j;

int nValueS[2][2]; // 用于存储块图像的属性值(该属性值= 该块图像的所有像素灰度值之和除以该块图像所有像素点的数量)

int nAV;

int nWidthTemp[3], nHeightTemp[3], nTemp;

int nWidth, nHeigh;

int n, m, l;

double dOver;

while(!nMyStack.empty())

{

splitStruct = nMyStack.top();

nMyStack.pop();

n = (splitStruct.nOffSetHeigh * nAllWidth + splitStruct.nOffSetWidth); // 该块图像的左上角

// 1. 把图像分成2 * 2 块,

nWidthTemp[0] = 0;

nWidthTemp[2] = (splitStruct.nWidth + 1) / 2;

nWidthTemp[1] = splitStruct.nWidth - nWidthTemp[2];

nHeightTemp[0] = 0;

nHeightTemp[2] = (splitStruct.nHeigh + 1) / 2;

nHeightTemp[1] = splitStruct.nHeigh - nHeightTemp[2];

// 计算每一块图像的属性值

int nValue;

int nValueTemp;

nAV = 0;

for(i = 1; i < 3; ++i)

{

for(j = 1; j < 3; ++j)

{

nValue = 0;

m = (n + nAllWidth * nHeightTemp[i - 1] + nWidthTemp[j - 1]);

for(nHeigh = 0; nHeigh < nHeightTemp[i]; ++nHeigh)

{

for(nWidth = 0; nWidth < nWidthTemp[j]; ++nWidth)

{

l = (m + nAllWidth * nHeigh + nWidth) * 4;

nValueTemp = (0.299 * image0[l] + 0.587 * image0[l + 1] + 0.114 * image0[l + 2]);

// 灰度值之和

nValue += nValueTemp;

}

}

if(nHeightTemp[i] * nWidthTemp[j] == 0)

{

continue;

}

if(nHeightTemp[i] * nWidthTemp[j] == 1)

{

l = m * 4;

if((0.299 * image0[l] + 0.587 * image0[l + 1] + 0.114 * image0[l + 2]) < 125)

// 这个值可以动态设定

{

image0[l] = image0[l + 1] = image0[l + 2] = 0;

image0[l + 3] = 255;

}

else

{

image0[l] = image0[l + 1] = image0[l + 2] = 255;

image0[l + 3] = 255;

}

continue;

}

// 各块图像的灰度平均值(每一块图像的属性值)

nValueS[i - 1][j - 1] = nValue / (nHeightTemp[i] * nWidthTemp[j]);

// 2. 对每一块进行判断是否继续分裂(注意分裂的原则)

// 我这里的分裂原则是: 图像的属性值在属性值平均值的误差范围之内就不分裂

if(nValueS[i - 1][j - 1] < 220) // 灰度平均值少于200 需要继续分裂 // 这里就是分裂准则了

{

splitStructTemp.nWidth = nWidthTemp[j];

splitStructTemp.nHeigh = nHeightTemp[i];

splitStructTemp.nOffSetWidth = splitStruct.nOffSetWidth + nWidthTemp[j - 1];

splitStructTemp.nOffSetHeigh = splitStruct.nOffSetHeigh + nHeightTemp[i - 1];

nMyStack.push(splitStructTemp);

}

else // 合并(直接填充该块图像为黑色)

{

// 3. 如果不需要分裂, 则进行合并

for(nHeigh = 0; nHeigh < nHeightTemp[i]; ++nHeigh)

{

for(nWidth = 0; nWidth < nWidthTemp[j]; ++nWidth)

{

l = (m + nAllWidth * nHeigh + nWidth) * 4;

image0[l] = image0[l + 1] = image0[l + 2] = 255;

image0[l + 3] = 255;

}

}

}

}

}

}

return;

}

该代码的效果也不是太好，主要是分裂准则不好确

区域分裂合并中 最初使用每块图像区域中极大与极小灰度值之差是否在允许的偏差范围来作为均匀性测试准则。 后来均匀性测试准则又被不断的发展。目前，统计检验，如均方误差最小， F检测等都是最常用的均匀性测试准侧方法

看均方误差最小的情况

其中C是区域R中N个点的平均值。

相对于区域生长而言，区域分割于合并技术不再依赖于种子点的选择与生长顺序。但选用合适的均匀性测试准则P对于提高图像分割质量十分重要，当均匀性测试准则P选择不当时，很容易会引起“方块效应”

参考连接;http://blog.csdn.net/bagboy_taobao_com/article/details/5666109

MATLAB

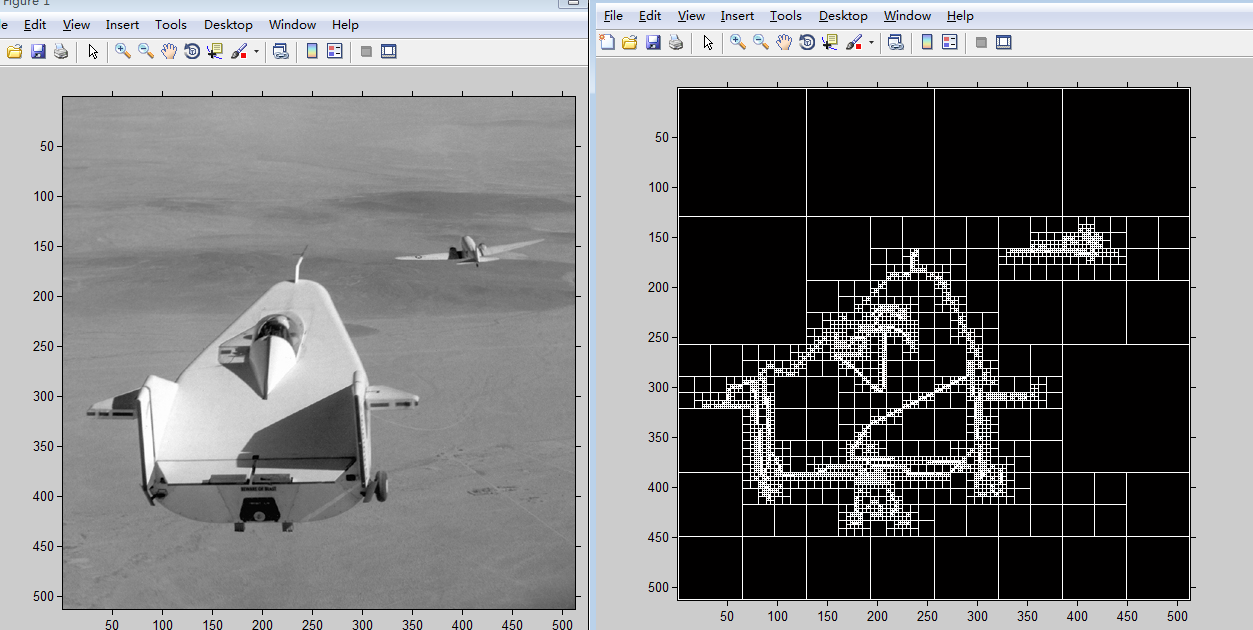
matlab中给出了qtdecomp().qtsetblk(),下面看看效果

I = imread('liftingbody.png');

S = qtdecomp(I,.27);%以阈值ceil(0.27*255)=69对图像I进行四叉分解

blocks = repmat(uint8(0),size(S));%得到一个和I同尺寸的黑色背景blocks

for dim = [512 256 128 64 32 16 8 4 2 1]; %分块全是2的整数次幂，注①

numblocks = length(find(S==dim)); %有numblocks个尺寸为dim的分块，注③

if (numblocks > 0)

values = repmat(uint8(1),[dim dim numblocks]);%产生一个dim x dim x numblocks的三维1值矩阵(或说

% numblocks个尺寸为dim x dim的1值block)

values(2:dim,2:dim,:) = 0;

blocks = qtsetblk(blocks,S,dim,values);%blocks保存了所有块被替换后的结果。注④

end

end

blocks(end,1:end) = 1;

blocks(1:end,end) = 1;

imshow(I), figure, imshow(blocks,[])

图像识别算法交流 QQ群：145076161，欢迎图像识别与图像算法，共同学习与交流

原文：http://blog.csdn.net/qq_20823641/article/details/52191210