1. 简单线性规划问题的有关概念
先来看一道高考题：
某公司招收男职员x名，女职员y名，x和y须满足约束条件
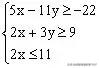
，则
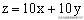
的最大值是( )
A. 80
B. 85
C. 90
D. 95
(1)约束条件：变量x、y满足的一组条件，如上面高考题中的二元一次不等式组
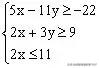
，就是对变量x、y的约束条件。
(2)线性约束条件：由变量x、y的一次不等式(或方程)组成的不等式组。如上面提到的二元一次不等式组中的约束条件都是关于x、y的一次不等式，所以又称为线性约束条件。
(3)目标函数：欲求最大值或最小值所涉及的变量x、y的解析式，如题中的
。
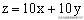
(4)线性目标函数：目标函数关于两个变量x、y的一次解析式，对于目标函数
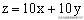
，变量x、y的次数都是一次，称为线性目标函数。
(5)线性规划问题：在线性约速条件下求线性目标函数的最大值或最小值的问题。如试题中在线性约束条件
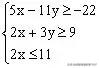
下，求线性目标函数z=10x+10y的最大值问题就是线性规划问题。
(6)可行解：满足线性约束条件的解(x，y)。
(7)可行域：由所有可行解组成的集合，如图1所示，△ABC的区域就称为可行域。
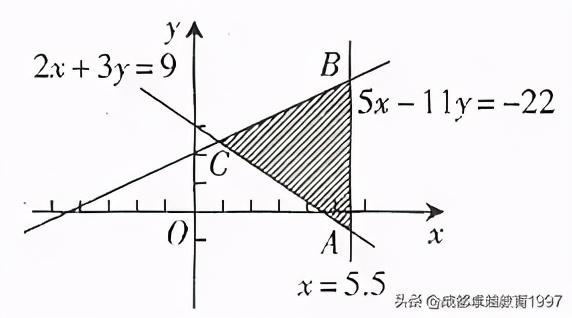
图1
(8)最优解：使目标函数取得最大值或最小值的可行解。
2. 线性规划问题的解题方法和步骤
解决简单线性规划问题的方法是图解法，即借助直线(线性目标函数看作斜率确定的一族平行直线)与平面区域(可行域)有交点时，直线在y轴上的截距的最大值或最小值求解，它的步骤如下：
(1)设出未知数，确定目标函数。
(2)确定线性约束条件，并在直角坐标系中画出对应的平面区域，即可行域。
(3)由目标函数
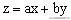
变形为
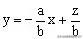
，所以求z的最值可看成是求直线
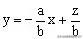
在y轴上截距的最值(其中a、b是常数，z随x、y的变化而变化)。
(4)作平行线：将直线
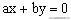
平移(即作
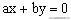
的平行线)，使直线与可行域有交点，且观察在可行域中使
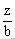
最大(或最小)时所经过的点，求出该点的坐标。
(5)求出最优解：将(4)中求出的坐标代入目标函数，从而求出z的最大(小)值。
3. 特别关注
(1)可行域就是二元一次不等式组表示的平面区域，可行域可能是封闭的多边形，也可能是一侧开放的无限大的平面区域。
(2)有些问题要求出最优解的整数解才符合实际情况，当解方程得到的解不是整数解时，常用下面的一些方法求解：
①平移直线法：先在可行域中画网格，再描整点，平移直线
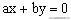
，最先经过或最后经过的整点坐标就是最优解。
②检验优值法：当可行域中整点个数较少时，可将整点坐标逐一代入目标函数求值，经过比较得出最优解。
③调整优值法：先求非整点的最优解，再借助于不定方程知识调整最优值，最后筛选出整点最优解。
4. 典题示例
例：某投资人打算投资甲、乙两个项目，根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损为30%和10%，投资人计划投资不超过10万元，要求确保可能的资金亏损不超过1.8万元。问投资人对甲、乙两个项目各投资多少万元，才可能使盈利最大？
解：设投资人分别将x万元，y万元投资于甲、乙两个项目。
由题意知
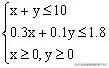
，目标函数
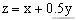
上述不等式组表示的平面区域如图2所示，阴影部分(含边界)即为可行域。
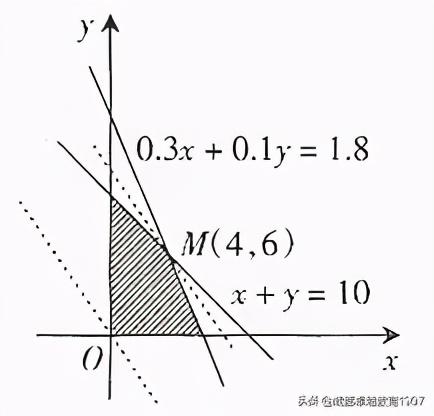
图2
将
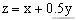
变为
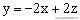
，则当直线
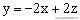
过点M时，在y轴上的截距最大，即z取得最大值。
解
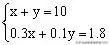
得
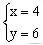
此时
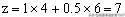
所以当x=4，y=6时，z取得最大值7。
故投资人用4万元资金投资甲项目、6万元投资乙项目，才能在确保亏损不超过1.8万元的前提下，使盈利最大。
...)
