点击关注我哦

autograd和动态计算图可以说是pytorch中非常核心的部分，我们在之前的文章中提到：autograd其实就是反向求偏导的过程，而在求偏导的过程中，链式求导法则和雅克比矩阵是其实现的数学基础；Tensor构成的动态计算图是使用pytorch的实现的结构。

backward()函数

backward()是通过将参数(默认为1x1单位张量)通过反向图追踪所有对于该张量的操作，使用链式求导法则从根张量追溯到每个叶子节点以计算梯度。下图描述了pytorch对于函数z = (a + b)(b - c)构建的计算图，以及从根节点z到叶子节点a,b,c的求导过程：

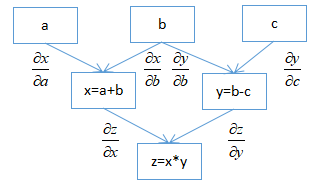
注意：计算图已经在前向传递过程中已经被动态创建了，反向传播仅使用已存在的计算图计算梯度并将其存储在叶子节点中。

为了节约内存，在每一轮迭代完成后，计算图就会被释放，若需要多次调用backward()方法，则需要在使用时添加retain_graph=True，否则会报如下错误：

RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed.

若我们在使用过程中，仅仅想求得某个节点的梯度，而非整个图的梯度，则需要用到Tensor的.grad属性，如下列代码所示：

import torch# 创建计算图x = torch.tensor(1.0, requires_grad = True)z = x ** 3# 计算梯度z.backward() print(x.grad.data)

需要注意的是：当调用z.backward()时，将自动计算z.backward(torch.tensor(1.0))，其中 torch.tensor(1.0)是用于终止连式法则梯度乘法的外部梯度。可以将此作为输入传递给MulBackward函数，以进一步计算x的梯度。

在上述的示例中，我们给出了标量对向量的求导过程，那么当向量对向量进行求导时呢？例如，需要计算梯度的张量x和y如下：

x = torch.tensor([0.0, 2.0, 8.0], requires_grad = True)y = torch.tensor([5.0 , 1.0 , 7.0], requires_grad = True)z = x * y

此时调用z.backward()函数将会报如下错误：

RuntimeError: grad can be implicitly created only for scalar outputs

错误提示我们只能应用于标量输出。若我们想对向量z进行梯度计算，先了解一下Jacobian矩阵。

Jacobian矩阵和向量

从数学角度上来讲：雅克比矩阵是基于函数对所有变量一阶偏导数的数值矩阵，当输入个数等于输出个数时又称为雅克比行列式。

而autograd类在实际运用的过程中也是通过计算雅克比向量积实现对向量梯度的计算。简单来说，雅可比矩阵是代表两个向量的所有可能偏导数的矩阵，可以用于求一个向量相对于另一个向量的梯度。

注：在此过程中，PyTorch不会显式构造整个Jacobian矩阵，而是直接计算Jacobian矢量积，这种计算方式更为简便。

如果向量X = [x1，x2，… xn]通过函数f(X)= [f1，f2，… fn]计算其他向量，假设f对于x的每个一阶偏导数都存在，则f(X)相对于X的梯度矩阵为：

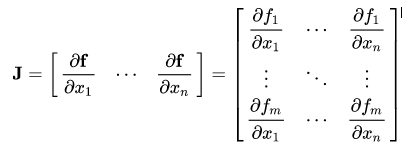
假设待计算梯度的张量X为：X = [x1，x2，… xn](机器学习模型的权重)，X可以进行一些运算以形成向量Y：Y = f(X)= [y1，y2，… ym]。然后，使用Y来计算标量损失l。假设向量v恰好是标量损失l相对于向量Y的梯度，则：

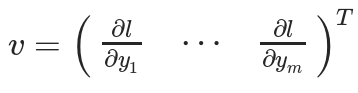
此时，向量v则被称为grad_tensor，即梯度张量。并将其作为参数传递给backward()函数。为了获得损失l相对于权重X的梯度，将Jacobian矩阵J与向量v相乘，得到最终梯度：

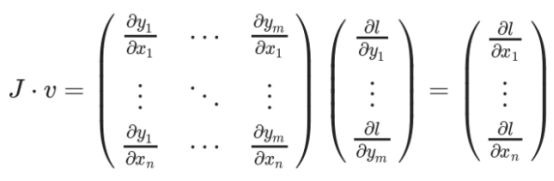
综上所述，pytorch在使用计算图求导的过程中整体可以分为以下两种情况：

1. 若标量对向量求导，则可以直接调用backward()函数；

2. 若向量A对向量B求导，则先求得向量A对于向量B的Jacobian矩阵，并将其与grad_tensors对应的矩阵进行点乘计算得到最终梯度。

·  END  ·

RECOMMEND推荐阅读

 1. 效率提升的软件大礼包

 2. 深度学习——入门PyTorch(一)

 3. 深度学习——入门PyTorch(二)

 4. PyTorch入门——autograd(一)

 5. PyTorch入门——autograd(二)