概述
上一篇讲述了《机器学习 | 算法笔记(三)- 支持向量机算法以及代码实现》,本篇讲述机器学习算法决策树,内容包括模型介绍及代码实现。
决策树
决策树(Decision Tree)在机器学习中也是比较常见的一种算法,属于监督学习中的一种。看字面意思应该也比较容易理解,相比其他算法比如支持向量机(SVM)或神经网络,似乎决策树感觉“亲切”许多。
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失值不敏感,可以处理不相关特征数据。
缺点:可能会产生过度匹配的问题。
使用数据类型:数值型和标称型。
划分数据集的大原则是:将无序的数据变得更加有序。
我们可以使用多种方法划分数据集,但是每种方法都有各自的优缺点。于是我们这么想,如果我们能测量数据的复杂度,对比按不同特征分类后的数据复杂度,若按某一特征分类后复杂度减少的更多,那么这个特征即为最佳分类特征。
下面,我们就对以下表格中的西瓜样本构建决策树模型。
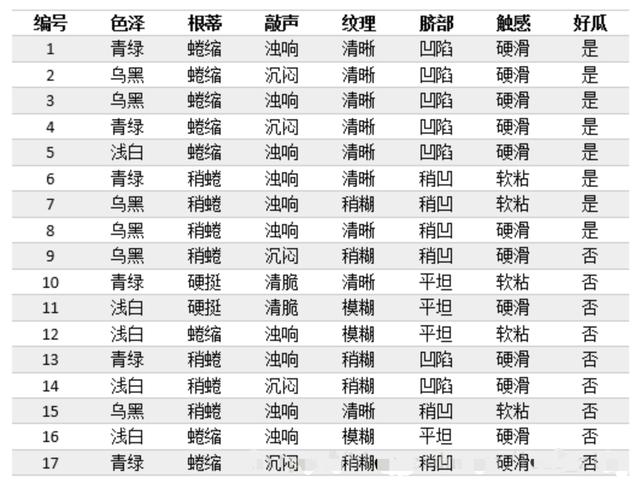
Claude Shannon 定义了熵(entropy)和信息增益(information gain)。
用熵来表示信息的复杂度,熵越大,则信息越复杂。
信息熵(information entropy)样本集合D中第k类样本所占的比例(k=1,2,...,|Y|),|Y|为样本分类的个数,则D的信息熵为:

Ent(D)的值越小,则D的纯度越高。直观理解一下:假设样本集合有2个分类,每类样本的比例为1/2,Ent(D)=1;只有一个分类,Ent(D)= 0,显然后者比前者的纯度高。
在西瓜样本集中,共有17个样本,其中正样本8个,负样本9个,样本集的信息熵为:

使用属性a对样本集D进行划分所获得的“信息增益”的计算方法是,用样本集的总信息熵减去属性a的每个分支的信息熵与权重(该分支的样本数除以总样本数)的乘积,通常,信息增益越大,意味着用属性a进行划分所获得的“纯度提升”越大。因此,优先选择信息增益最大的属性来划分。
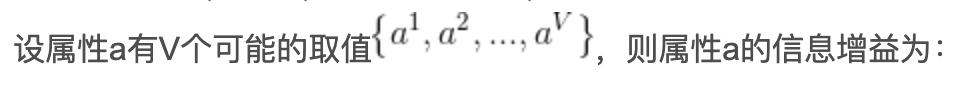


同理也可以计算出其他几个属性的信息增益,选择信息增益最大的属性作为根节点来进行划分,然后再对每个分支做进一步划分。
用python构造决策树基本流程

决策树学习基本算法
ID3算法与决策树的流程
(1)数据准备:需要对数值型数据进行离散化
(2)ID3算法构建决策树:
- 如果数据集类别完全相同,则停止划分
- 否则,继续划分决策树:
计算信息熵和信息增益来选择最好的数据集划分方法;划分数据集创建分支节点:对每个分支进行判定是否类别相同,如果相同停止划分,不同按照上述方法进行划分。
通常一棵决策树包含一个根节点、若干个分支节点和若干个叶子节点,叶子节点对应决策结果(如好瓜或坏瓜),根节点和分支节点对应一个属性测试(如色泽=?),每个结点包含的样本集合根据属性测试的结果划分到子节点中。
我们对整个训练集选择的最优划分属性就是根节点,第一次划分后,数据被向下传递到树分支的下一个节点,再这个节点我们可以再次划分数据,构建决策树是一个递归的过程,而递归结束的条件是:所有属性都被遍历完,或者每个分支下的所有样本都属于同一类。
还有一种情况就是当划分到一个节点,该节点对应的属性取值都相同,而样本的类别却不同,这时就把当前节点标记为叶节点,并将其类别设为所含样本较多的类别。例如:当划分到某一分支时,节点中有3个样本,其最优划分属性为色泽,而色泽的取值只有一个“浅白”,3个样本中有2个好瓜,这时我们就把这个节点标记为叶节点“好瓜”。
代码实现
数据集:https://download.csdn.net/download/li1873997/12671852
trees.py
from math import logimport operator # 此行加在文件顶部# 通过排序返回出现次数最多的类别def majorityCnt(classList): classCount = {} for vote in classList: if vote not in classCount.keys(): classCount[vote] = 0 classCount[vote] += 1 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) return sortedClassCount[0][0]# 递归构建决策树def createTree(dataSet, labels): classList = [example[-1] for example in dataSet] # 类别向量 if classList.count(classList[0]) == len(classList): # 如果只有一个类别,返回 return classList[0] if len(dataSet[0]) == 1: # 如果所有特征都被遍历完了,返回出现次数最多的类别 return majorityCnt(classList) bestFeat = chooseBestFeatureToSplit(dataSet) # 最优划分属性的索引 bestFeatLabel = labels[bestFeat] # 最优划分属性的标签 myTree = {bestFeatLabel: {}} del (labels[bestFeat]) # 已经选择的特征不再参与分类 featValues = [example[bestFeat] for example in dataSet] uniqueValue = set(featValues) # 该属性所有可能取值,也就是节点的分支 for value in uniqueValue: # 对每个分支,递归构建树 subLabels = labels[:] myTree[bestFeatLabel][value] = createTree( splitDataSet(dataSet, bestFeat, value), subLabels) return myTree# 计算信息熵def calcShannonEnt(dataSet): numEntries = len(dataSet) # 样本数 labelCounts = {} for featVec in dataSet: # 遍历每个样本 currentLabel = featVec[-1] # 当前样本的类别 if currentLabel not in labelCounts.keys(): # 生成类别字典 labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 shannonEnt = 0.0 for key in labelCounts: # 计算信息熵 prob = float(labelCounts[key]) / numEntries shannonEnt = shannonEnt - prob * log(prob, 2) return shannonEnt# 划分数据集,axis:按第几个属性划分,value:要返回的子集对应的属性值def splitDataSet(dataSet, axis, value): retDataSet = [] featVec = [] for featVec in dataSet: if featVec[axis] == value: reducedFeatVec = featVec[:axis] reducedFeatVec.extend(featVec[axis + 1:]) retDataSet.append(reducedFeatVec) return retDataSet# 选择最好的数据集划分方式def chooseBestFeatureToSplit(dataSet): numFeatures = len(dataSet[0]) - 1 # 属性的个数 baseEntropy = calcShannonEnt(dataSet) bestInfoGain = 0.0 bestFeature = -1 for i in range(numFeatures): # 对每个属性技术信息增益 featList = [example[i] for example in dataSet] uniqueVals = set(featList) # 该属性的取值集合 newEntropy = 0.0 for value in uniqueVals: # 对每一种取值计算信息增益 subDataSet = splitDataSet(dataSet, i, value) prob = len(subDataSet) / float(len(dataSet)) newEntropy += prob * calcShannonEnt(subDataSet) infoGain = baseEntropy - newEntropy if (infoGain > bestInfoGain): # 选择信息增益最大的属性 bestInfoGain = infoGain bestFeature = i return bestFeature# 计算信息熵def calcShannonEnt(dataSet): numEntries = len(dataSet) # 样本数 labelCounts = {} for featVec in dataSet: # 遍历每个样本 currentLabel = featVec[-1] # 当前样本的类别 if currentLabel not in labelCounts.keys(): # 生成类别字典 labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 shannonEnt = 0.0 for key in labelCounts: # 计算信息熵 prob = float(labelCounts[key]) / numEntries shannonEnt = shannonEnt - prob * log(prob, 2) return shannonEnt# 划分数据集,axis:按第几个属性划分,value:要返回的子集对应的属性值def splitDataSet(dataSet, axis, value): retDataSet = [] featVec = [] for featVec in dataSet: if featVec[axis] == value: reducedFeatVec = featVec[:axis] reducedFeatVec.extend(featVec[axis + 1:]) retDataSet.append(reducedFeatVec) return retDataSet# 选择最好的数据集划分方式def chooseBestFeatureToSplit(dataSet): numFeatures = len(dataSet[0]) - 1 # 属性的个数 baseEntropy = calcShannonEnt(dataSet) bestInfoGain = 0.0 bestFeature = -1 for i in range(numFeatures): # 对每个属性技术信息增益 featList = [example[i] for example in dataSet] uniqueVals = set(featList) # 该属性的取值集合 newEntropy = 0.0 for value in uniqueVals: # 对每一种取值计算信息增益 subDataSet = splitDataSet(dataSet, i, value) prob = len(subDataSet) / float(len(dataSet)) newEntropy += prob * calcShannonEnt(subDataSet) infoGain = baseEntropy - newEntropy if (infoGain > bestInfoGain): # 选择信息增益最大的属性 bestInfoGain = infoGain bestFeature = i return bestFeature下面使用西瓜样本集,测试一下算法,创建一个WaterMalonTree.py文件。因为生成的树是中文表示的,因此使用json.dumps()方法来打印结果。如果是不含中文,直接print即可。
# -*- coding: cp936 -*-import treesimport json fr = open(r'C:Python27pyDecisionTreewatermalon.txt') listWm = [inst.strip().split('') for inst in fr.readlines()]labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']Trees = trees.createTree(listWm, labels) print json.dumps(Trees, encoding="cp936", ensure_ascii=False)运行该文件,打印出西瓜的决策树,它是一个字典:
{"纹理": {"模糊": "否", "清晰": {"根蒂": {"稍蜷": {"色泽": {"乌黑": {"触感": {"软粘": "否", "硬滑": "是"}}, "青绿": "是"}}, "蜷缩": "是", "硬挺": "否"}}, "稍糊": {"触感": {"软粘": "是", "硬滑": "否"}}}}
总结
决策树是一种基于树结构来进行决策的分类算法,我们希望从给定的训练数据集学得一个模型(即决策树),用该模型对新样本分类。决策树可以非常直观展现分类的过程和结果,一旦模型构建成功,对新样本的分类效率也相当高。
最经典的决策树算法有ID3、C4.5、CART,其中ID3算法是最早被提出的,它可以处理离散属性样本的分类,C4.5和CART算法则可以处理更加复杂的分类问题,本文重点介绍ID3算法。下一篇介绍通过《 数据可视化-Python实现Matplotlib绘制决策树》。











![短信宝 php使用,[php] 使用 短信宝 发送短信(thinkphp)](http://pic.xiahunao.cn/短信宝 php使用,[php] 使用 短信宝 发送短信(thinkphp))







