例题中有2019年罗马尼亚大师赛第3试题

树

树：一个连通图，如果没有一个环，则叫树。

森林：若干个独立的树形成一个森林。

链：一个特殊的树是节点中，除去两个节点的度为1，其它均为2，叫做链。

二叉树：如果一个树只有一个节点的度为2，其它的节点的度要么为3，要么为1，那这样的树叫二叉树。

树，链，二叉树之所以重要是因为这些图可以灵活表达计算机内部基本数据结构。例如我们打开一个应用软件，按下一个功能键，会有菜单弹出或者窗口弹出，管理这些菜单与窗口最好的办法是将其组织成树结构。链是计算机内部维护一个动态数组的最佳结构，通过插入，删除节点，只需要修改边指针，而不需要真实移动数据。二叉树可以做分类，编译。能够灵活运用这些基本结构，并用程序语言表达出来，是程序员的基本功。那些年薪几十万，上百万的程序员对此都有相关的知识与运用经验，而习得这些经验与做数学习题差不多，也许更简单一点，就是要多编写程序，但题量会大一点，要求格式更严谨一点而已。

不论是树还是链，其顶点数如果是n的话，边数一定是n-1.

定理：n个顶点，n-1条边的图一定是树。

证明：用归纳法

n=1，命题成立

假设

n=k时命题也成立，我们看n=k+1的情况，考虑k+1个顶点，k+1条边这样的图中的一条最长路径，如果有一个端点a，如果d(d)>1,则必然有环，因为否则的话，可以添加一条边到这条最长路径中，使得新路径长度为增加1.删去节点a，设与a相邻的一个节点为b，同时删除边{a，b}，就剩下k个节点，k-1条边的连通图了，按归纳假设这是棵树，故n=k+1时命题成立。

例题1.考虑平面的若干点，任意两点之间的直线段长度都不相同，如果将每个点与其距离最近的点连成一条直线段，求证:所画出的线段不会形成一个封闭的多边形。

证明：

首先将这些点当成一个图的顶点，按题设的办法将做了的直线段对应成图的一条边，形成图G，假设G中有环。

如下图

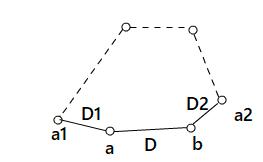
由于任意两点之间的直线距离最短，故这个环路上所有边对应的直线段长度均不相同，不妨设最长的线段长度为D，对应边为{a，b}，设a1是与a相邻的顶点，a2是与b相邻的顶点，边{a，a1}，{b，b2}对应的线段长度分别为D1，D2，则D>D1,D2.故从a出发做出的直线段不能为b，从b出发的直线段也不能为a。也就是说按题设根本做不出边{a，b}来。因此这个图中没有环路。

但即使没有环路，也可能有如下图这样两种方式形成闭合的图形。

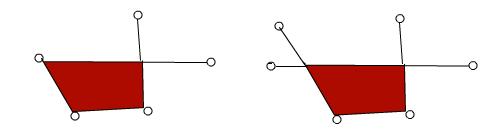
我们接下来证明，按题目要求做出的直线段是不能出现交叉现象的。

反证法

假设作出的线段，如下图出现了交叉

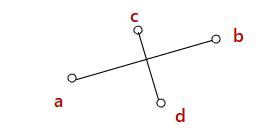
虚线连接a，d；d，b；b，c；c，a

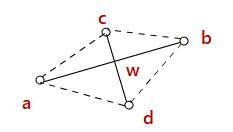
则按照题设直线段的做法有：

ab

4ab2ab+2dc

另一方面，设ab，cd相交于w点

则：

wa+cw>ac,wc+wb>cb,wb+wd>bd,wd+wc>ad

相加得

2ab+2cd>ab+bc+cd+da矛盾

这就证明本题。

割边：如果一个连通图中去掉一个边，就成为非连通的了，这条边叫连通图的一条割边。对于树来说，没条边都是割边。

生成树：若图G的的一个子图T包含所有的顶点，且为一棵树，则称T为图G的生成树。

在图G中而不在生成树T中的边，称为对应于树T的弦，所有弦的集合是树T的补，弦的数目就是图G的圈数，记作N(G)，树枝的数目称为图的秩，记作及R(G)。如果G有n个结点m条边，则R(G)＝n-1，N(G)＝m-n+l。R(G)＋ N(G)=m。

生成树的算法

去圈法：

如果连通图G无回路，根据的定义，则G本身就是一棵生成树。如果连通图G有回路，去掉回路的任一条边得到生

成子图G1，显然G1仍然是连通的，如果G1不含回路，则G1就是G的生成树，否则又可去掉回路的任一条边得到另一个生成子图，只要生成图还有回路，就去掉回路的一条边，由于图的有限性，最后一定得到不含回路的生成子图T，由于每次去掉回路的一条边，并不破坏图的连通性，所以T是G的生成树。这种办法可以产生图的生成树。

生长法：在G中任找一条边e1，然后找一条不与e1形成回路的边e2，再找一条不与边集合(e1,e2)形成回路的边e3，如此继续下去使找的边都不与已找到的边集合形成回路，直到过程不能进行下去为止，则所有找到的边集

合{e1,e2,e3,...,em}构成的图就是G的一棵生成树。

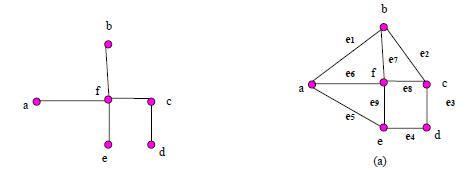
设T是图G的一棵生成树，由T的树枝和一条弦构成的回路称为对应于这条弦的基本回路，基本回路的集合，称为基本回路集。如左图是右图的一棵生成树则对应于

弦e1的基本回路是C(e1)＝{e1,e6,e7}

对应于弦e2的基本回路是C(e2)＝{e2,e7,e8}

对应于弦e4的基本回路是C(e4)＝{e4,e3,e8,e9}

对应于弦e5基本回路是C(e5)＝{e5 e6 e9}

树T的基本回路集是C＝{C(e1)C(e2)C(e3)C(e4)}

如果我们给图上的每个边赋权，那么就得到一个赋权的图。例如结点是城市,边的权表示两个城市间的距离,

从一个城市出发走遍各个城市,如何选择最优的旅行路线.又如城市间的通信网络问题,如何布线,使得总的线路长度最短，等等就是要找一棵生成树，且使得生成树的边权的和最小。这样的生成树叫最小生成树。

最小生成树的Kruskal算法:

设G是有n个结点,m条边(m≥n-1)的连通图.

1.将所有边按照权升序排序:e1, e2, e3,… ,em，T=Φ

2.i=1.。。。。。m做如下操作

如果T∪{ ei }有回路，则去掉ei，返回2

T=T∪{ ei };

如果i=n，T就是最小生成树，结束

否则i++，返回2.

例题2.连通图G中每条边赋予一个数，设c为最小值，如果G中存在一个具有s条边的基本回路，求证：这个图至少有s个不同的最小生成树。

证明：利用上面的kruskal算法，中间 的支撑树集合T，在选前s-1条边时，必然都是从这个基本回路中选出的边，从s个边中，每次选s-1条边，总计有s种不同的选法。而这s个s-1条边的集合各不相同，所以最终生成的最小生成树至少也有s个。

做为高中联赛题目，不说kruskal算法，直接求证本题，应该是不算太难的题。那就需要把kruskal算法的基本思想先说清楚，然后再填上上面的答案，才能得分。这是常见的高联出题方法。

一个连通图G的顶点数为n，边数为e，则生成树的边为n-1，故弦数为e-(n-1)=e-n+1，每个弦对应于一个基本回路。

所以有定理：顶点数+基本回路数=n-1+e-n+1=e。

线性电路基本分析方程

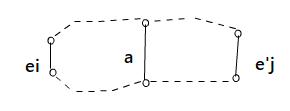
假设一个电路图，只有电池与电阻元件，总计为e个，电路图上的每个元件对应于图的一条边，直连不同元件的线路端点，收缩为成一个顶点，总计有n个顶点。下图表达简单的电路图变换成图论中的图。

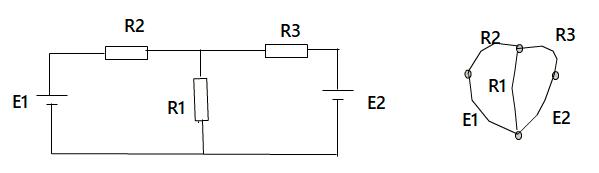
根据基尔霍夫定律，流入流出一个节点(顶点)的电流代数和为0，任意一个电路回路的电压代数和为0。注意到一个树中，每个节点连出的边不完全相同，可以形成n-1个独立的电流方程。每个基本回路都有一条弦是唯一的，可以形成e-n+1个独立的回路电压方程，用电阻乘以电流代表一个电阻元件的电压，只要这些电阻阻值确定，电池电压确定，就可得到e个独立的以流过每个元件电流为变量的一次方程组，这个方程组是有唯一解的。这就是电路分析的基本方法，也是图论理论的一个来源，而现今是现代集成电路CAD软件分析中，研究电路电气响应特性的核心方法。

树搜索算法

深度优先搜索算法(DFS)

深度优先搜索的基本思想是在搜索其它他顶点之前，尽可能深地渗透到树的深层中。这个想法可以描述如下：

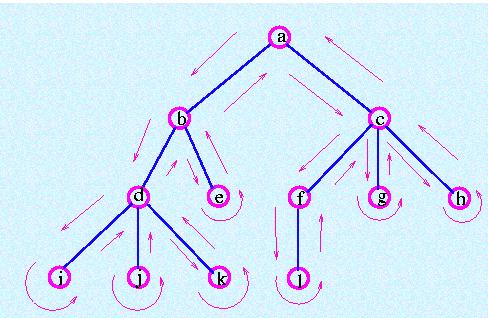
处理次序：a -> b --> d --> i -> j -> k -> e -> c -> f -> i -> g -> h

宽度优先搜索算法(BFS)

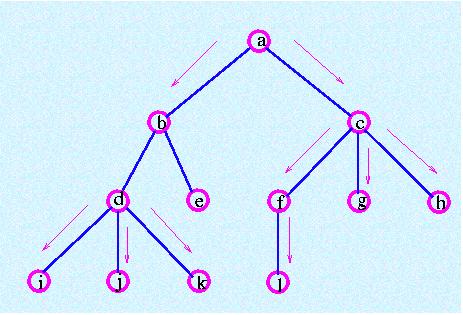
宽度优先搜索的基本思想是在深入到树中之前，尽可能多地处理上层顶点。这个想法可以描述如下：