文章目录
- 0 赛题思路
- 1 模型描述
- 2 实例
- 2.1 问题描述
- 2.2 数学模型
- 2.2.1 模型流程
- 2.2.2 符号约定
- 2.2.3 求解模型
- 2.3 相关代码
- 2.4 模型求解结果
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
最短时间生产计划模型
该模型出现在好几个竞赛赛题上,预测2023今年国赛也会与该模型相关。
1 模型描述
离散系统仿真在工业生产的工序安排中起到了相当重要的作用,如何就一些内部机制复杂的离散问题建立简单易行、可监测性强的数学模型一直是仿真技术的研究热点.
离散事件系统现有三种仿真建模策略,即:
- 事件调度法
- 活动扫描法
- 进程交互法.
该模型demo学长采用了其中的活动扫描法对生产中的一个实际例子进行了处理.
活动扫描法对于各事件之间相关性很强的系统有着很好的适用性.
2 实例
2.1 问题描述
在许多工厂生产过程中,由于设备的数量、产品加工的次序限制,往往不能简单地安排生产任务.我们设想,应用强大的数学软件配合简单易行的方法进行安排.
设某重型机械厂产品都是单件性的,其中有一车间共有4种不同设备,现接受6件产品的加工任务,每件产品接受的程序在指定的设备上加工,其工序与加工周期如下表

现在我们根据这一实际问题,寻求安排的方法.
要求:
1、每件产品必须按规定的工序加工,不得颠倒.
2、每台设备在同一时间只能担任一项任务(每件产品的每个工序为一个任务).
3、在尽可能短的时间里,完成所接受的全部任务.
为了节省电能,合理分配生产任务,厂方还要求:
1、做出每件产品的每个工序开工、完工时间表.
2、给出每台设备承担任务的时间表.
2.2 数学模型
2.2.1 模型流程

2.2.2 符号约定

2.2.3 求解模型
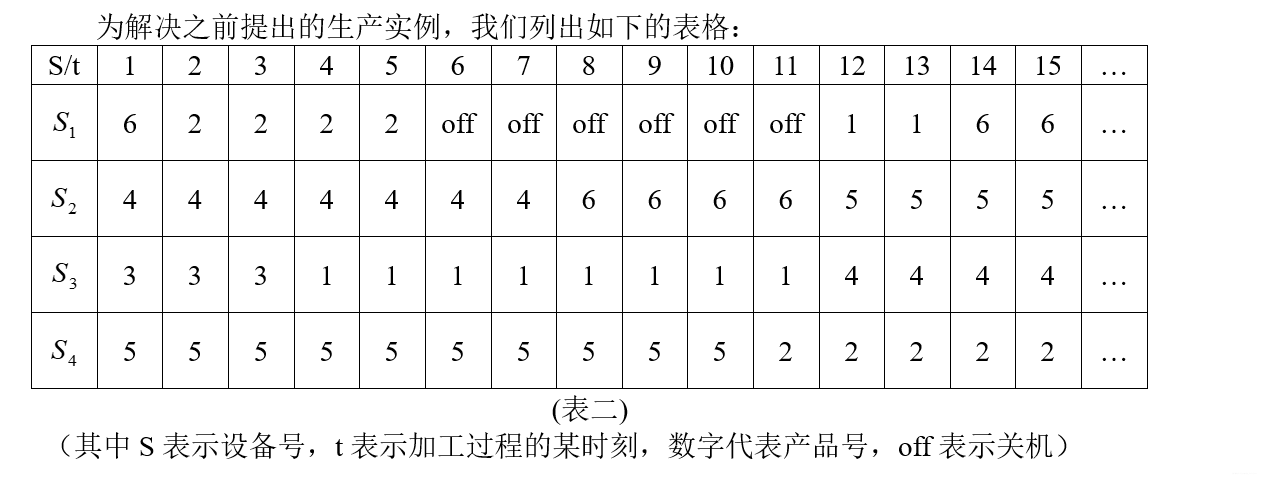
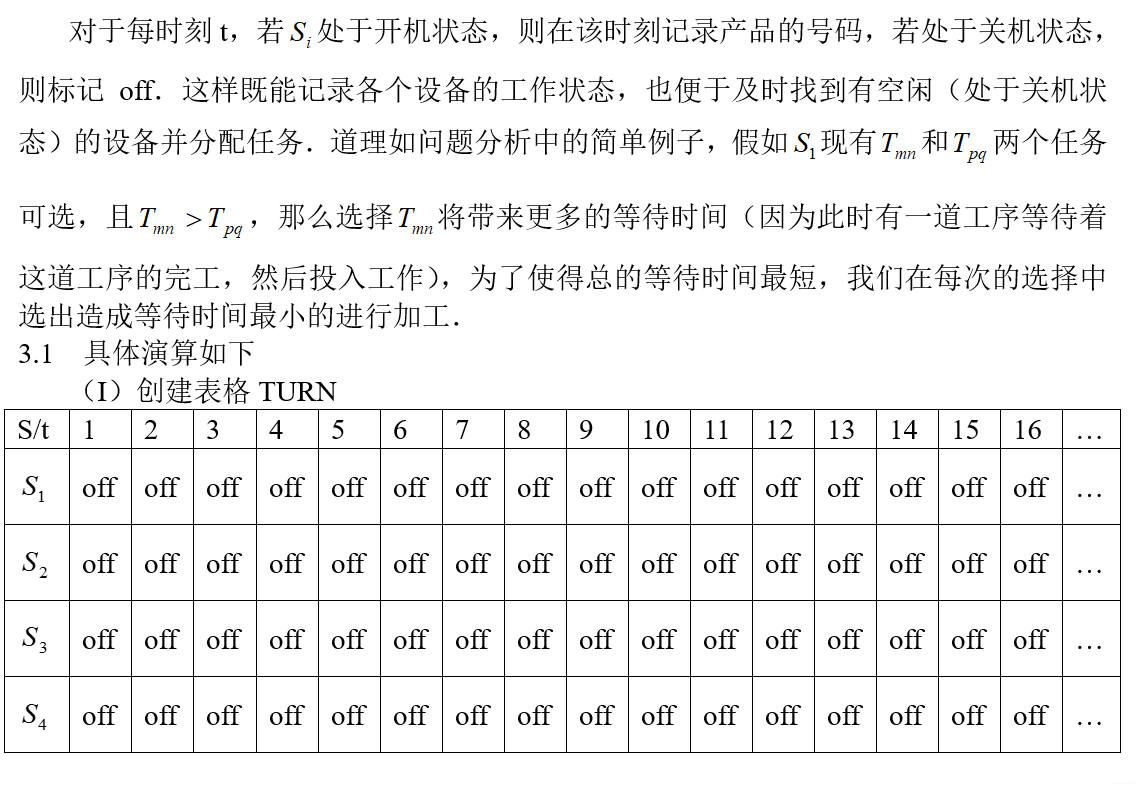
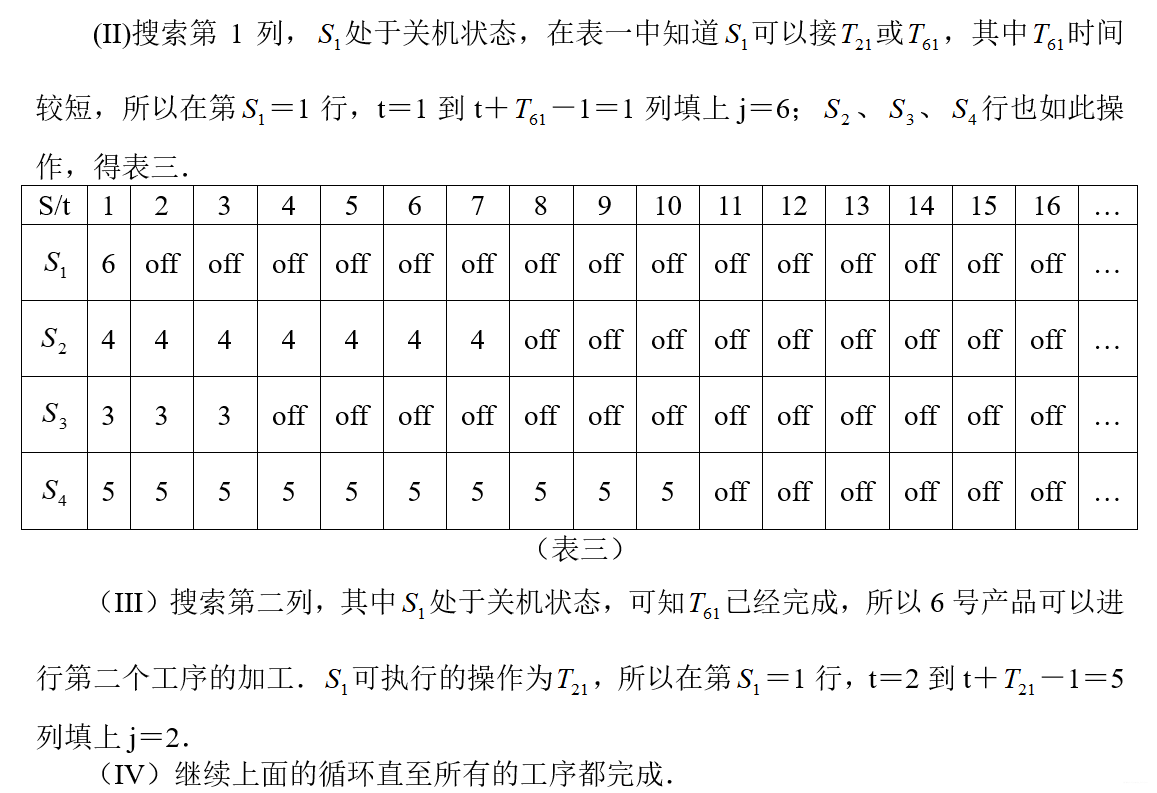
2.3 相关代码
clear
clc
seq=[3 1 2 3 4 0 0 0 %各产品加工时所用的设备的次序1 4 2 3 0 0 0 03 4 1 2 1 0 0 02 3 4 1 4 3 0 04 2 3 4 1 3 4 01 2 1 3 4 1 3 1];tim=[8 2 4 24 6 0 0 0 %加工对应使用的时间4 5 3 4 0 0 0 03 7 15 20 8 0 0 07 6 21 1 16 3 0 010 4 8 4 12 6 1 01 4 7 3 5 2 5 8];
whole=[0 0 0 0];
for i=1:6for j=1:8if(seq(i,j)~=0)whole(seq(i,j))=whole(seq(i,j))+tim(i,j);endend
end
whole %生产各件产品所需的总时间mes=cell(4,1); %记录各个设备的工作时间(对应于上面tim的位置)
for k=1:4mes{k,1}=zeros(6,8);for j=1:8for i=1:6if(seq(i,j)==k)mes{k,1}(i,j)=tim(i,j);elsemes{k,1}(i,j)=100;endendend
endturn=cell(5,100); %记录四个设备的开关时间及加工对象(on(i))
for i=1:4for j=1:100turn{i,j}='off';end
end
for i=1:100turn{5,i}=[num2str(i) '分'];
endopen=zeros(6,8);
%记录6个产品的加工进度,0表示未进行,1表示已开始(或已结束),2表示可选,3表示没有这个程序
for i=1:6open(i,1)=2;
end
for i=1:6for j=1:8if seq(i,j)==0open(i,j)=3;endend
endgongxu=zeros(6,1);
dai=zeros(4,1);
j=1;
s=[1 1 1 1 1 3 3 3
1 1 1 1 3 3 3 3
1 1 1 1 1 3 3 3
1 1 1 1 1 1 3 3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1];
while isequal(open,s)==0on=[];for i=1:4if turn{i,j}=='off'
%在turn矩阵中逐列搜索,若设备处于关机状态,则作记录(可用)on=[on i];endendl1=length(on);for m=1:l1 %在整个生产计划中(对设备逐个)寻找能够选作操作的步骤[x,y]=find(open==2);l2=length(x);a=[x(1) y(1)];for k=1:l2 %对某个设备on(m),找出当前它能操作的步骤中耗时最小的一个if mes{on(m)}(a(1),a(2))>mes{on(m)}(x(k),y(k))a=[x(k) y(k)];endendif turn{on(m),j}=='off' & mes{on(m)}(a(1),a(2))~=100
%若时间为100则意味着这个步骤不属于我们希望使用的那件设备while tim(a(1),a(2))>0turn{on(m),tim(a(1),a(2))+j-1}=a(1);tim(a(1),a(2))=tim(a(1),a(2))-1;endendendfor i=1:4if turn{i,j}~='off'dai(i)=turn{i,j};endendfor i=1:4if turn{i,j}~='off' & turn{i,j+1}=='off'gongxu(turn{i,j})=gongxu(turn{i,j})+1;open(turn{i,j},gongxu(turn{i,j}))=1;endif gongxu(dai(i))<8 & open(dai(i),gongxu(dai(i))+1)~=3 & turn{i,j+1}=='off'open(dai(i),gongxu(dai(i))+1)=2;endendj=j+1;
end2.4 模型求解结果
每件产品的每个工序开工、完工时间表

每台设备承担任务的时间表
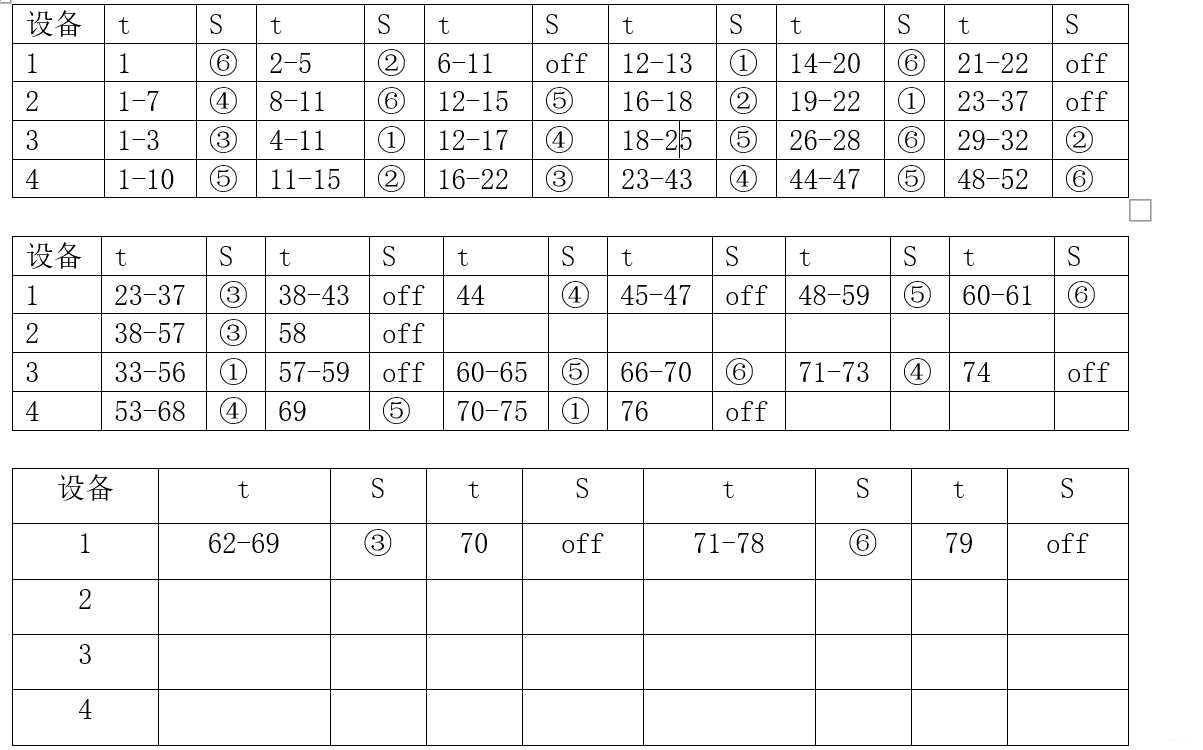
从结果中我们可以看到,使用这种方法,只需78个单位时间就可以完成所有的工序.而我们同时也可以在论文的开始部分看到,单就完成 就需耗费75个单位时间.可见这种方法得出的结果还是相当使人满意的,而且操作简单,可监测性强.
建模资料
资料分享: 最强建模资料




)



)



)

)






