Root 林鳞 编译自 DeepMind官方博客
量子位 出品 | 公众号 QbitAI

随着人工智能系统在现实世界中扮演越来越重要的角色，理解不同的系统如何相互作用至关重要。

刚刚，DeepMind发表了一篇名为Symmetric Decomposition of Asymmetric Games的论文。在这篇论文中，DeepMind研究人员采用了博弈论的分支试图这个问题。

研究人员重点观察了在德州扑克，棋盘游戏苏格兰特警等非对称博弈中，两个智能体会有怎样的行为和表现。

用这种新方法，智能体能简单快速地在复杂的非对称博弈里找到纳什均衡。

博弈与纳什均衡

博弈论属于数学的一个分支，用于分析竞争环境下决策者的策略。

这套理论适用于人类，动物，以及超过一个AI时的多AI环境。比如说家里多个机器人同时打扫房间。

非对称信息博弈模拟了真实世界的场景，就像拍卖时买家和卖家的心态和动机不同。我们得到的结果给了我们独道的见解，以及极其简洁的方式分析他们。

非对称博弈的特点是每方玩家都有不同的策略、目标和奖励。比如说博弈论研究里最常见的协调博弈，性别之战。

一般来说，多AI系统的进化动态过程是用简单的对称博弈来分析，比如说经典的囚徒困境，两方玩家都可以采取同样的行动。即使这些博弈能够为多AI系统提供有效的洞见，告诉我们如何操作所有玩家才能获得最优结果（这就是纳什均衡），但他们并不能模拟出所有的情况。

DeepMind的新的方法，能简单快速地在复杂的非对称博弈里找到纳什均衡。

虽然目前这套理论的重点还在如何应用在多个AI系统的互动中，但研究人员相信这个结论也可以用于经济、进化生物学、经验博弈论中。

歌剧还是电影？

举个例子吧。

两名玩家需要决定晚上是去看歌剧还是电影，不巧的是，其中一名偏好歌剧而另一名偏好电影。这是场不对称的游戏，虽然两名玩家可以任意选择，但是根据玩家的喜好，每个玩家得到奖励是不同的。

但是，为了维持他们的友谊，或者我们称为一种平衡，双方需要选择相同的活动，因此单独行动的回报为零。

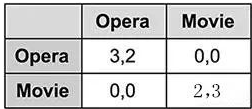
这个游戏有三个平衡：(i)双方都去看歌剧，(ii)双方去看电影，(iii)还有一个混合选项，每个玩家在五分之三的时间里选择他们喜欢的选项。

这个“不稳定的”的最后一个选项，就是用了将不对称游戏简化或分解成它的对称对等体的方法。

我们可以将这种游戏的本质想象成，每个玩家的奖励分数表是一个独立对称的双玩家游戏，它的平衡点与原始的不对称游戏一致。

在下面这张图中，纳什均衡是通过两个对等点得到的，帮助我们快速确定不对称博弈中的最优策略(a)。反过来说，利用不对称博弈来确定对称对等点的均衡。

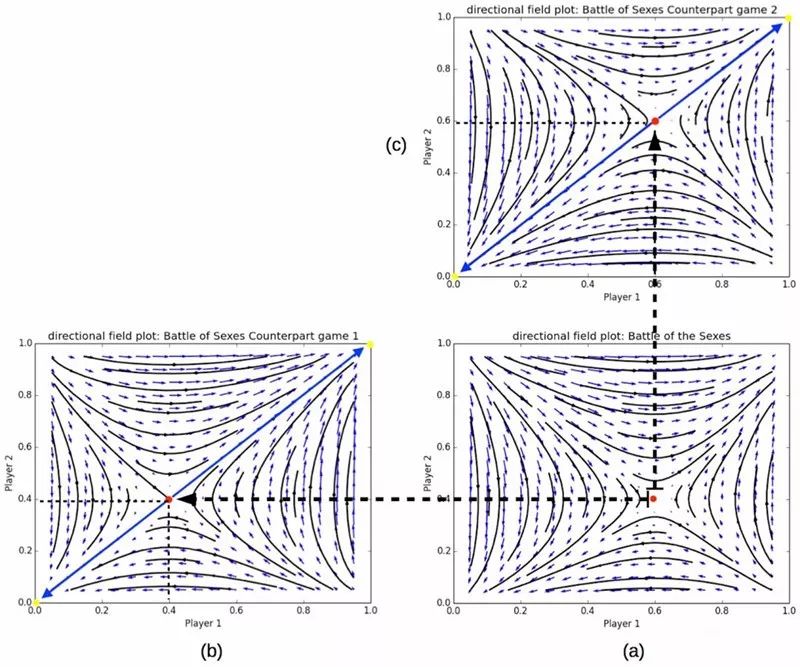
△ 红点代表纳什均衡。对于不对称的游戏(a)，纳什均衡可以很容易地从(b)和(c)两张对称图中得到。上述图中，x、y轴分别为玩家1、2选择歌剧的概率

好消息是，这种方法也适用于其他游戏，比如Leduc扑克等。这些方法应用了一个简单的数学原理，从而快速直接分析不对称游戏。我们希望它也能帮助我们理解各种动态系统，包括多代理环境。

最后，附论文地址：

https://www.nature.com/articles/s41598-018-19194-4

未来智能实验室是人工智能学家与科学院相关机构联合成立的人工智能，互联网和脑科学交叉研究机构。由互联网进化论作者，计算机博士刘锋与中国科学院虚拟经济与数据科学研究中心石勇、刘颖教授创建。

未来智能实验室的主要工作包括：建立AI智能系统智商评测体系，开展世界人工智能智商评测；开展互联网（城市）云脑研究计划，构建互联网（城市）云脑技术和企业图谱，为提升企业，行业与城市的智能水平服务。

  如果您对实验室的研究感兴趣，欢迎加入未来智能实验室线上平台。扫描以下二维码或点击本文左下角“阅读原文”