目前为止,我们探讨了单变量/特征的回归模型,现在我们对房价模型增加更多的特征, 例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为(x1,x2,…,xn)

增添更多特征后,我们引入一系列新的注释:
n 代表特征的数量
$x^{(i)}$代表第 i 个训练实例,是特征矩阵中的第 i 行,是一个向量(vector)。
$x^i_j$ 代表特征矩阵中第 i 行的第 j 个特征,也就是第 i 个训练实例的第 j 个特征。

支持多变量的假设 h 表示为:$h(x)= \theta_0+\theta_1x_1+\theta_2x_2... \theta_nx_n$

这个公式中有 n+1 个参数和 n 个变量,为了使得公式能够简化一些,引入 x0=1,则公式
转化为:$h(x)=\Theta^TX$

多变量梯度下降

与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价 函数是所有建模误差的平方和,即:

$$j(\theta_0,\theta_1...\theta_n)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$$
其中: $h_\theta(x)=\Theta^TX=\theta_0x_0+\theta_1x_1+....\theta_nx_n$

我们的目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数。
多变量线性回归的批量梯度下降算法为:

梯度下降法实践 1-特征缩放

在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯 度下降算法更快地收敛。
以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0- 2000 平方英尺,而房间数量的值则是 0-5,以两个参数分别为横纵坐标,绘制代价函数的等 高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。

解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。

$$x_n=\frac{x_n-u_n}{s_n}$$
其中 $u_n$表示平均值， $s_n$表示标准差

梯度下降法实践 2-学习率
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,我们不能提前预知,我们 可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

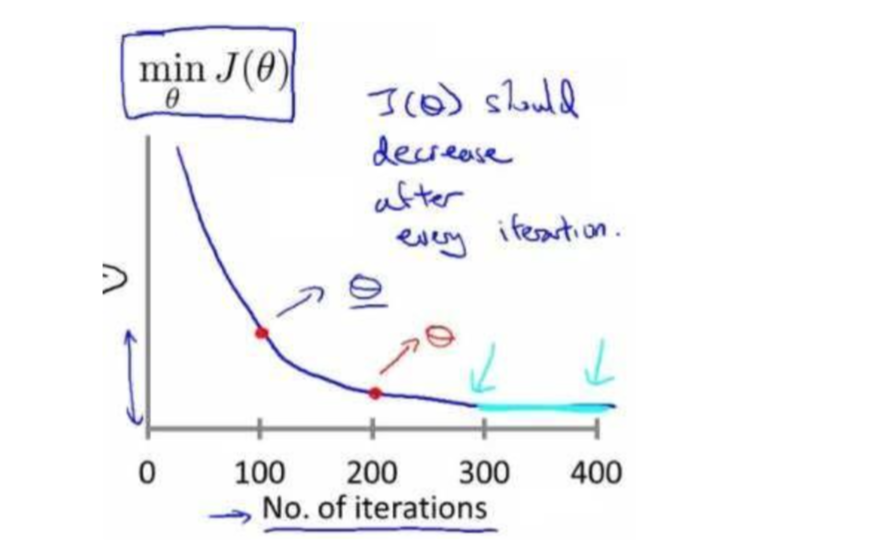
也有一些自动测试是否收敛的方法,例如将代价函数的变化值与某个阀值(例如 0.001) 进行比较,但通常看上面这样的图表更好。
梯度下降算法的每次迭代受到学习率的影响,如果学习率 α 过小,则达到收敛所需的迭 代次数会非常高;如果学习率 α 过大,每次迭代可能不会减小代价函数,可能会越过局部最 小值导致无法收敛。

通常可以考虑尝试些学习率: α=0.01,0.03,0.1,0.3,1,3,10

特征和多项式回归

注:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。

正规方程

正规方程是通过求解下面的方程来找出使得代价函数最小的参数的: $\frac{\sigma}{\sigma\theta_j}J(\theta_j)=0$

假设我们的训练集特征矩阵为 X(包含了 x0=1)并且我们的训练集结果为向量 y,则利用正规方程解出的向量为

$$\Theta=(X^TX)^{-1}X^Ty$$

注:对于那些不可逆的矩阵(通常是因为特征之间不独立,如同时包含英尺为单位的尺
寸和米为单位的尺寸两个特征,也有可能是特征数量大于训练集的数量),正规方程方法是 不能用的。

梯度下降与正规方程的比较:

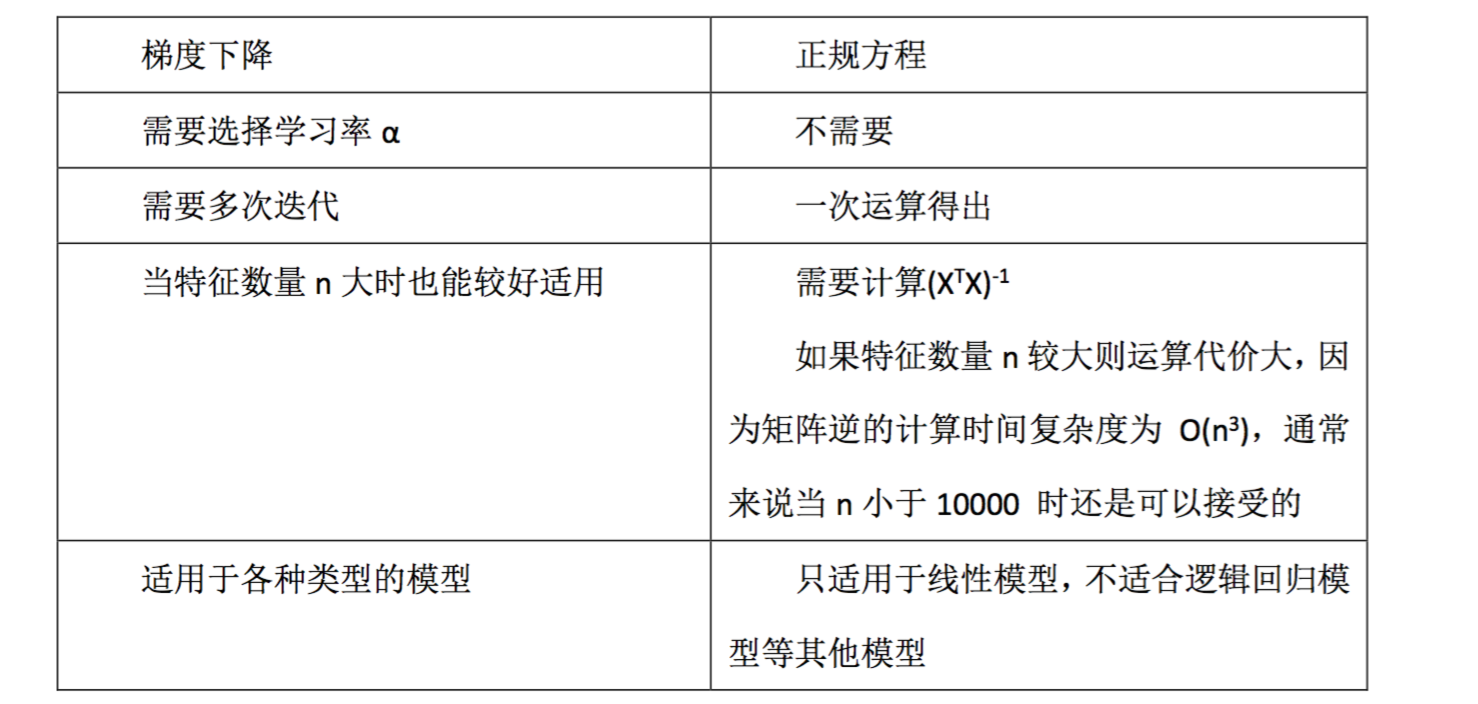
总结一下,只要特征变量的数目并不大,标准方程是一个很好的计算参数 θ 的替代方 法。具体地说,只要特征变量数量小于一万,我通常使用标准方程法,而不使用梯度下降法。
随着我们要讲的学习算法越来越复杂,例如,当我们讲到分类算法,像逻辑回归算法,
我们会看到, 实际上对于那些算法,并不能使用标准方程法。对于那些更复杂的学习算法,
我们将不得不仍然使用梯度下降法。因此,梯度下降法是一个非常有用的算法,可以用在有大量特征变量的线性回归问题

正规方程及不可逆性

有些同学曾经问过我,当计算 θ=inv(X’X ) X’y ,那对于矩阵 X’X 的结果是不可逆的情况 咋办呢?
如果你懂一点线性代数的知识,你或许会知道,有些矩阵可逆,而有些矩阵不可逆。我 们称那些不可逆矩阵为奇异或退化矩阵。

问题的重点在于 X’X 的不可逆的问题很少发生,在 Octave 里,如果你用它来实现 θ 的 计算,你将会得到一个正常的解。在 Octave 里,有两个函数可以求解矩阵的逆,一个被称 为 pinv(),另一个是 inv(),这两者之间的差异是些许计算过程上的,一个是所谓的伪逆,另 一个被称为逆。使用 pinv() 函数可以展现数学上的过程,这将计算出 θ 的值,即便矩阵 X’X 是不可逆的。

在 pinv() 和 inv() 之间,又有哪些具体区别呢 ?
其中 inv() 引入了先进的数值计算的概念。例如,在预测住房价格时,如果 x1 是以英尺 为尺寸规格计算的房子,x2 是以平方米为尺寸规格计算的房子,同时,你也知道 1 米等于 3.28 英尺 ( 四舍五入到两位小数 ),这样,你的这两个特征值将始终满足约束:x1=x2* (3.28)2。

实际上,你可以用这样的一个线性方程,来展示那两个相关联的特征值,矩阵 X’X 将是 不可逆的。

第二个原因是,在你想用大量的特征值,尝试实践你的学习算法的时候,可能会导致矩 阵 X’X 的结果是不可逆的。
具体地说,在 m 小于或等于 n 的时候,例如,有 m 等于 10 个的训练样本也有 n 等于
100 的特征数量。

总之,出现不可逆矩阵的情况极少发生,所以 在大多数实现线性回归中,出现不可逆的问题不应该过多的关注 XTX 是不可逆的。