1.矩阵和向量线性变换

线性变换可看着是对空间的挤压伸展。

也就是看成把向量中的值对矩阵列向量加权 ,在对向量求和

 2.矩阵和矩阵的线性变换

矩阵左乘就是对行向量操作，矩阵右乘就是对列向量操作． 

可以将其中一个矩阵看成是多个列向量,在拆开对剩下矩阵执行1操作

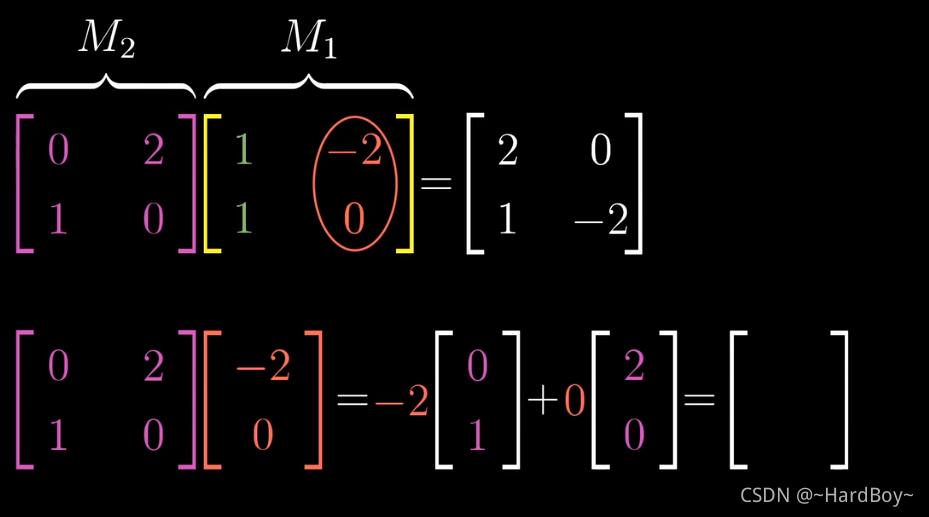
3.三维变换

绕y轴旋转后的旋转向量

 即由

[[1,0,00,1,00,0,1]]

 变为

[[0,0,10,1,0-1,0,0]]

4.行列式

如何量化变换对空间的挤压，拉伸？

如下,线性变换面积增加6倍。 

a表示对x轴拉伸，b表示对y拉伸 

 如下,线性变换面积不变。  

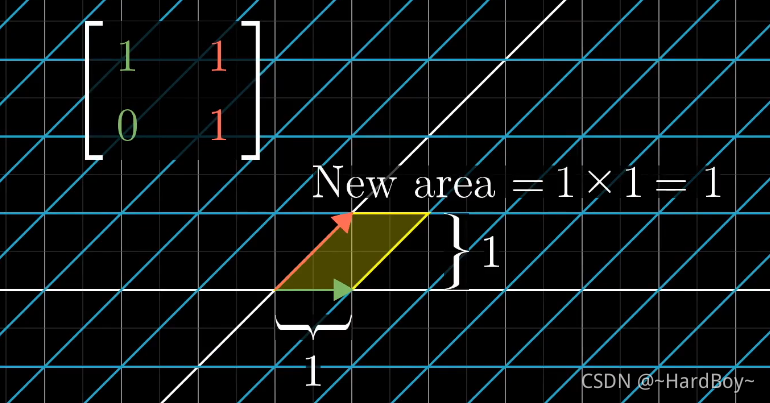
线性变换改变面积的比例就被称为行列式

行列式为0,说明平面被拉伸到线甚至点。

行列式为负表示空间被翻转，但是绝对值仍然表示面积比例

 

三张图展示这个过程，假设j不动,i移动

  

 而行列式对于三维空间就是体积缩放，也就是平行六面体体积。

 

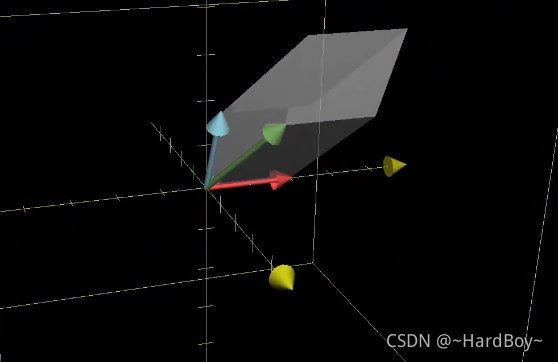
 而三维行列式为0,则成一个面或者线甚至点，就说明了线性相关。

5.线性方程组理解

A已经表示一种线性变换了，其是就是寻找向量x去，使得A变换后与v重合。

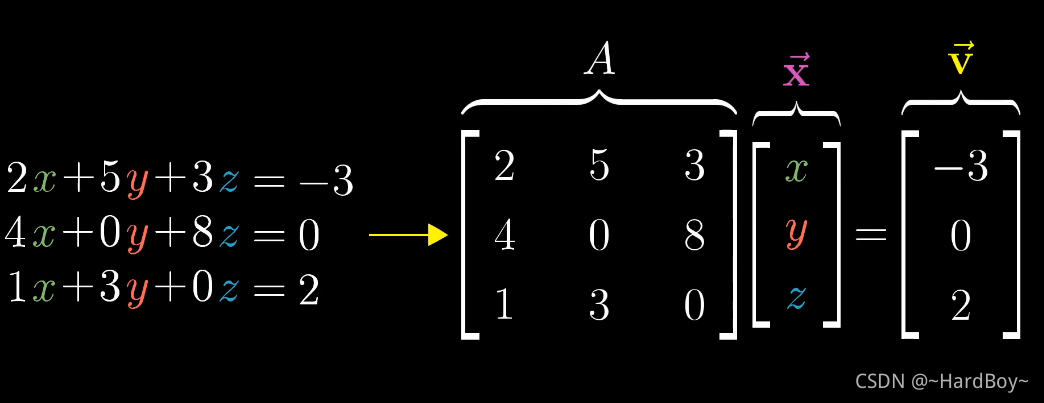
6.逆矩阵

其实就是逆向变换跟踪v的动向回到x

但是如果行列式为0,不可能存在逆矩阵，也就是线段不可能解压缩为平面。

7.秩与列空间

如果3维空间经过变换为二维平面说明此时矩阵秩为2,如果变为直线，说明矩阵秩为1.也就是秩代表变换后空间维数。

而列空间表示的是所有可能的变换结果的集合。秩也可以理解为列空间的维数。

也可以理解为矩阵的列张成的空间。

8.点积

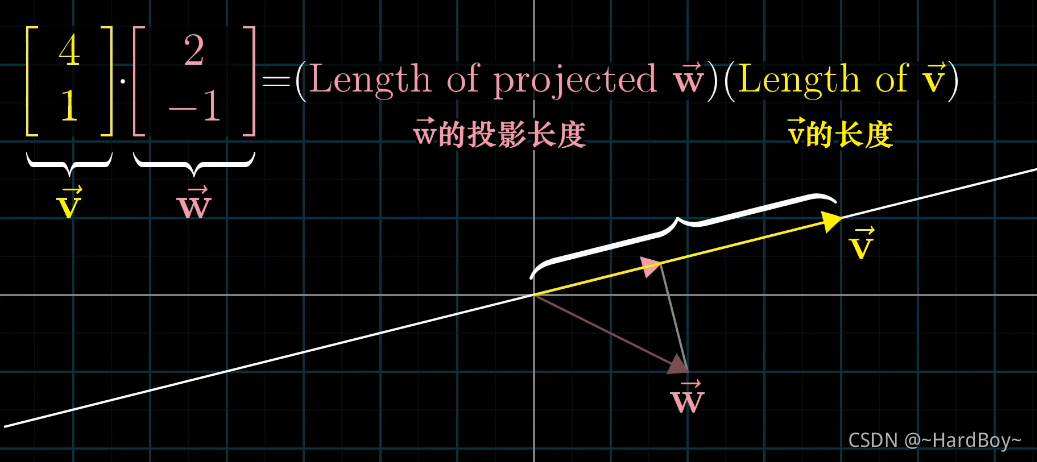
9.叉积

对于二维向量叉积就是行列式值(面积)在加上右手定则得出方向

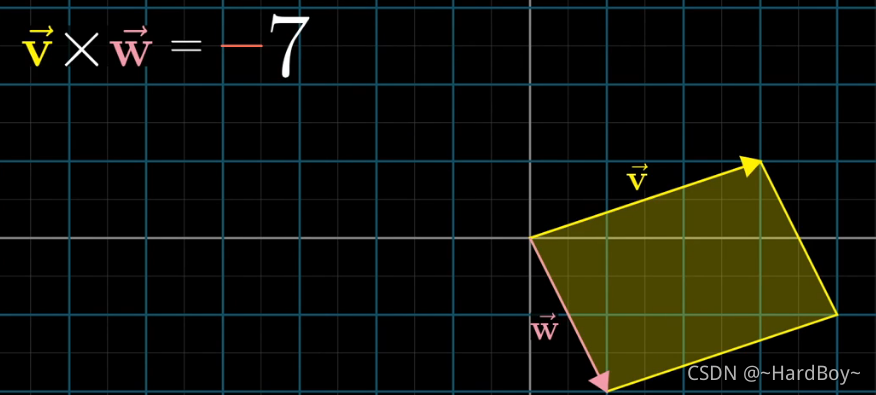
对于三维

10.基变换

 虽然都关注同一组向量，但选择的基向量不一样，导致向量值不一样。

需要表示一组基向量到另一组基向量变化。 

例如：如下图，在他的坐标系下的[-1, 2]T,对应到常用的坐标系就是[-4, 1]T,

也就是:

[[1, 0  [[-4
[0, 1]]  1]]

一种线性变换。 

求他的坐标系下[-1, 2]T逆时针转换后的向量 ,其中

[[2, -1[1, 1]]

是基变换矩阵，目的是将他的坐标系下向量对齐到标准坐标系下，在左乘一个旋转矩阵，在乘回基变换矩阵的逆就是他的坐标系下的向量的选择逆时针旋转90 度。

整理出来就是如下：A表示的是基变换矩阵，M表示的是对齐的坐标系下的变换矩阵。 

 

11.特征向量与特征值

 也就是当v为非零向量时，求解使得的行列式为0（对应上面就是平行六面体体积为0）,需要降维。

参考:从【官方双语/合集】线性代数的本质 - 系列合集_哔哩哔哩_bilibili