2. 图像的几何变换
图像几何变换是指用数学建模的方法来描述图像位置、大小、形状等变化。图像几何变换是图像处理及分析的基础。
-
图像的几何变换包括:图像平移、比例缩放、旋转和图像插值。
-
图像几何变换的实质:改变像素空间位置或估算新空间位置上的像素值。
-
图像变换的一般表达式:[u,v] = [X(x,y),Y(x,y)]
- 其中[u,v]为变换后图像像素的笛卡尔坐标,[x,y]为原始图像中像素的笛卡尔坐标。这样就得到了原始图像变换后图像的像素的对应关系。
- 如果说 X(x,y)=x, Y(x,y)=y, 则有[u,v]=[x,y],即变换后图像仅仅是原图像的简单拷贝。
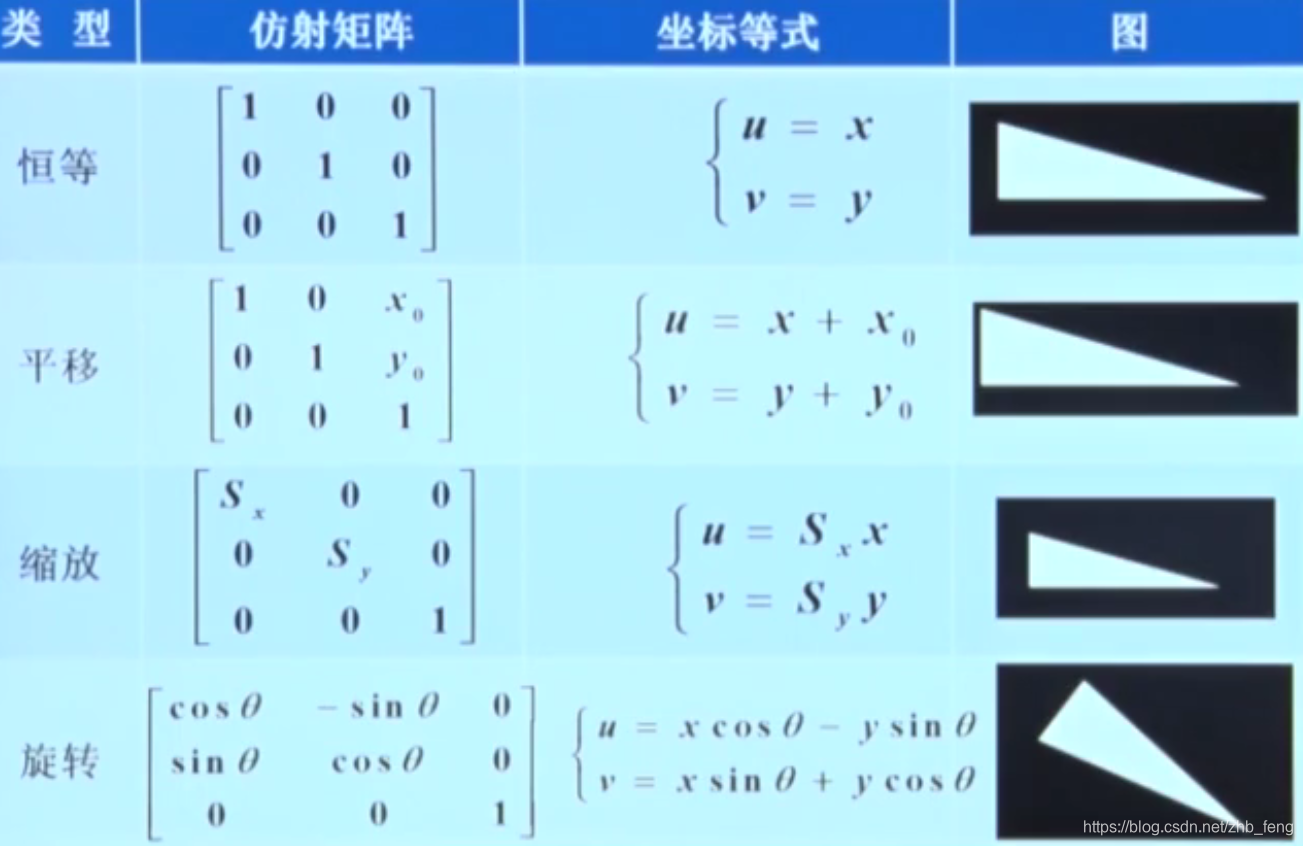
2.1 平移变换
若图像像素点 [x,y] 平移到 [x+x0,y+y0],则变换函数为:
- u = X(x,y) = x+x0
- v = Y(x,y) = y+y0
其中,x0 和 y0 分别是 x和y的坐标平移量。
写成矩阵表达式为:
2.2 比例缩放
若图像坐标 [x,y] 缩放到 (Sx,Sy) 倍,则变换函数为:
- u = Sx x
- v = Sy y
其中,Sx,Sy 分别为x和y坐标的缩放因子,其中大于1表示放大,小于1表示缩小。
写成矩阵表达式为:

2.3 旋转变换
将输入图像绕笛卡尔坐标系的原点逆时针旋转 θ 角度,则变换后图像坐标为:

图像旋转变换示例:

2.4 仿射变换
放射变换是一种二维坐标到二维坐标之间的线性变换,可保持二维图形的“平直性”和“平行性”。
- 平直性:一条直线在仿射变换后,仍然是一条直线,不会把它映射成一个圆弧或者其他的。
- 平行性:两条平行的直线,在放射变换后仍然是平行的,不会相交。
仿射变换的一般表达式为:

平移、比例缩放和旋转变换都是一种称为仿射变换的特殊情况。
上式可以表示成如下的线性表达式

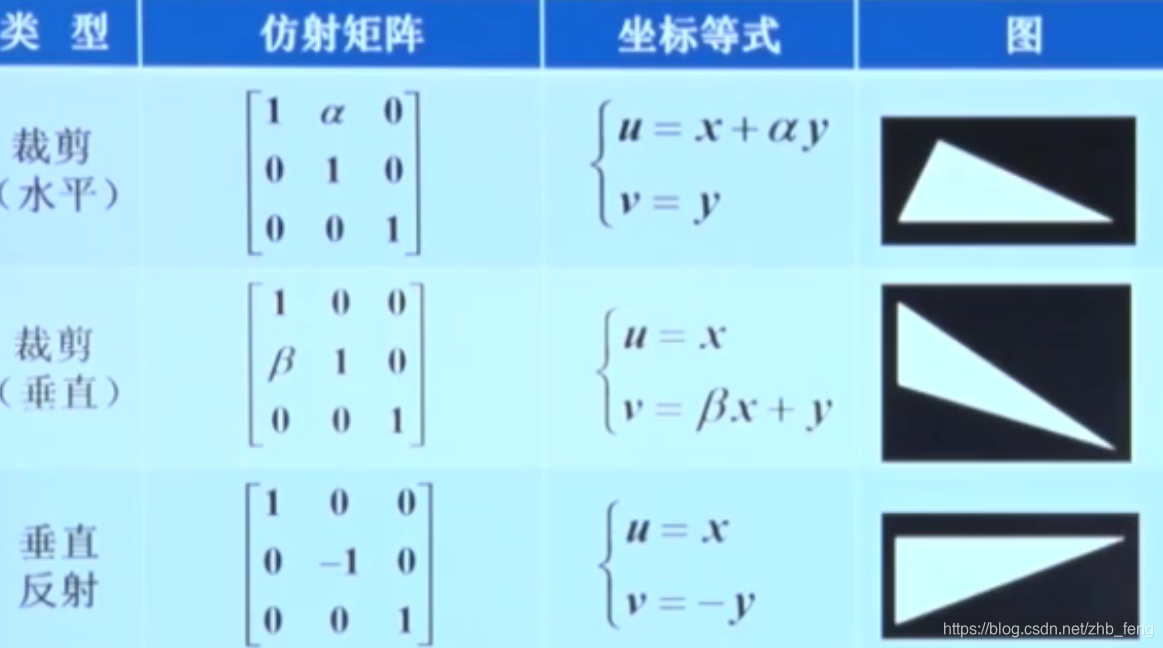
设定加权因子 ai 和 bi 的值,可以得到不同的变换。例如,当选定 a2 = b1 = 1 , b2 = -0.1 ,
a1 = a0 = b0 = 0,这种情况是图像剪切的一种情况。
仿射变换也可以用 3*3 的矩阵来表示:

仿射变换具有如下性质:
1)放射变换只有6个自由度(对应变换的6个系数),因此,仿射变换后互相平行的直线仍然为平行直线,三角形映射后仍然是三角形。但却不能保证将四边形以上的多边形映射为等边数的多边形。
2)仿射变换的乘积和逆变换仍是放射变换。
2.5 透视变换
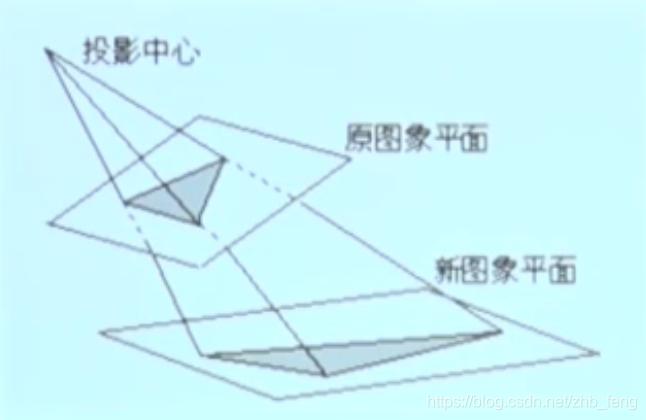
与之前仿射变换不同,透视投影按照从投影中心这一点发出的直线将物体投影到平面。
透视变换也是一种平面映射,称为透视变换,也称为投影映射,其表达式为:

并且可以保证任意方向上的直线经过透视变换后仍然保持直线。
透视变换具有9个自由度(其变化系数为9个),故可以实现平面四边形到四边形的映射。
图例:


2.6 插值
灰度插值
1)最近邻插值法:也称作零阶插值,也就是令变换后的像素的灰度值等于距它最近的输入像素的灰度值。
 基于最近邻点概念的灰度级插值。
基于最近邻点概念的灰度级插值。
特点:计算简单。但当图像中的像素灰度级有细微变换时,该方法会在图像中产生人工的痕迹。比如,轻微的马赛克现象。
2)双线性插值也称作一阶插值:
该方法通常是沿图像矩阵的每一列(行)进行插值,然后对插值后所得到的矩阵再沿着行(列)方向进行线性插值。

特点:当对相邻四个像素点采用双线性插值时,所得表面在邻域处吻合的,但斜率不吻合。并且双线性灰度插值的平滑作用可能使得图像的细节产生退化,这种现象在进行图像放大是尤其明显。
3)卷积插值法:当图像放大时,图像像素的灰度值插值可以通过卷积来实现,即,将输入图像两行两列中间插零值,然后通过低通模板滤波。

一般低通模板有:
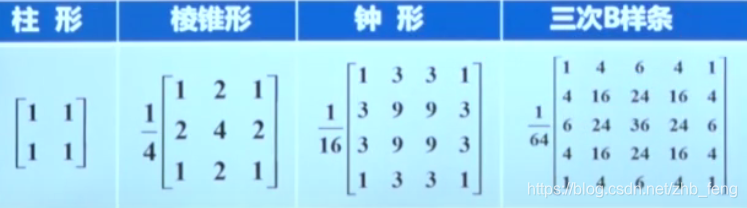





的五种模式)






递归成树状结构)
)





