这次笔记简单介绍图像梯度、梯度图以及梯度算子的概念，并详细介绍三种基本的梯度算子，然后简单的介绍Canny检测的原理与代码实现（因为Canny检测中有很重要的一步用到了Sobel算子计算梯度，所以先介绍前面的内容）。

一、图像梯度

1.1 梯度

先来看梯度的概念：

梯度是一个向量，梯度方向指向函数变化最快的方向，大小就是它的模，也是最大的变化率，对于二元函数z=f(x,y)，它在点(x,y)的梯度记为：

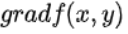
或：

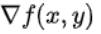
梯度的计算公式为：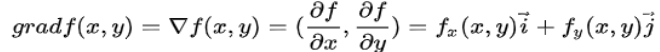
梯度向量的幅值和方向角为：

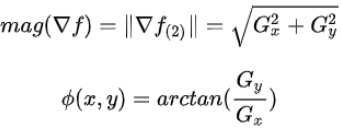
有了梯度是最大变化率这么一个认识，下面我们拓展到图像梯度的概念上来。

1.2 图像梯度

图像梯度即图像中灰度变化的度量，求图像梯度的过程是二维离散函数求导过程。

因为图像边缘上的像素值变化非常剧烈，所以图像的边缘其实就是图像上灰度级变化很快的点的集合。

下图展示了一个灰度图的数学化表达，像素点(x,y)的灰度值是f(x,y),它有八个邻域（有时使用四邻域）：

图像在点(x,y)的梯度为：

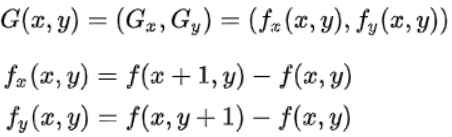
分别对应图像的水平方向和竖直方向，可见图像梯度的求法只是像素值之间的差，而无需求导（因为数字图像是离散的）。

二、梯度图与梯度算子

2.1模板卷积

要理解梯度图的生成，就要先了解模板卷积的过程，模板卷积是模板运算的一种方式，其步骤如下：

1. 将模板在输入图像中漫游，并将模板中心与图像中某个像素位置重合；
2. 将模板上各个系数与模板下各对应像素的灰度相乘；
3. 将所有乘积相加（为保持灰度范围，常将结果再除以模板系数之和，后面梯度算子模板和为0的话就不需要除了）；
4. 将上述运算结果（模板的响应输出）赋给输出图像中对应模板中心位置的像素。

其实就是现在的卷积运算干的事。

2.2 梯度图

梯度图的生成和模板卷积相同，不同的是要生成梯度图，还需要在模板卷积完成后计算在点(x,y)梯度的幅值，将幅值作为像素值，这样才算完。

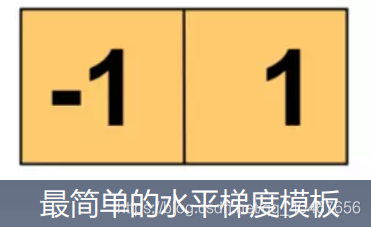
注意： 梯度图上每个像素点的灰度值就是梯度向量的幅度，生成梯度图需要两个模板（求图像梯度需要两个方向），右图为水平和竖直方向最简单的模板：

所以水平方向和竖直方向上的梯度为：

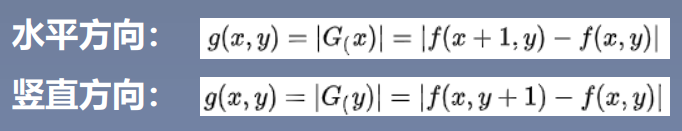
2.3 梯度算子

梯度算子是一阶导数算子，是水平G(x)和竖直G(y)方向对应模板的组合，也有对角线方向，即是上述卷积模板的组合。

常见的一阶算子：Roberts交叉算子， Prewitt算子， Sobel算子，下面将分别介绍。

2.3.1 Roberts交叉算子

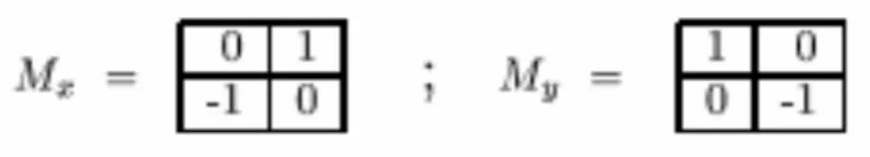
Roberts交叉算子其本质是一个对角线方向的梯度算子，对应的水平方向和竖直方向的梯度分别为：

优点：边缘定位较准，适用于边缘明显且噪声较少的图像。
缺点：

1. 没有描述水平和竖直方向的灰度变化，只关注了对角线方向，容易造成遗漏。
2. 鲁棒性差。由于点本身参加了梯度计算，不能有效的抑制噪声的干扰。

2.3.2 Prewitt算子

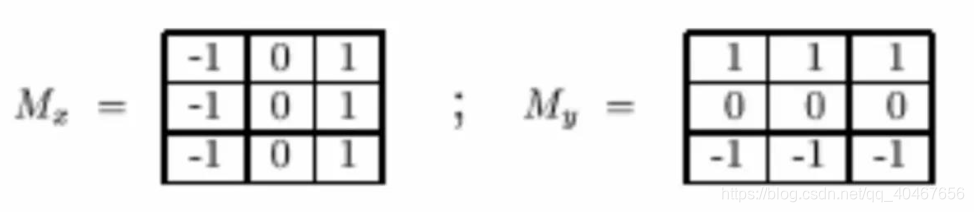
Prewitt算子是典型的3*3模板，其模板中心对应要求梯度的原图像坐标(x,y)， (x,y)对应的8-邻域的像素灰度值如下表所示：

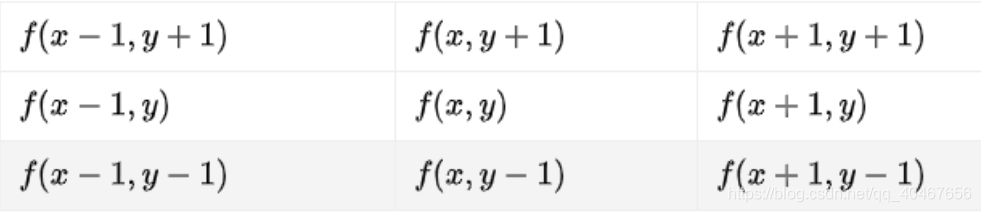
通过Prewitt算子的水平模板M(x)卷积后，对应的水平方向梯度为：

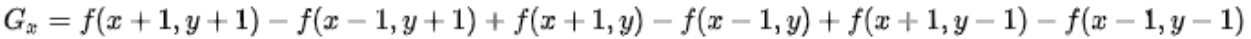
通过Prewitt算子的竖直模板M(y)卷积后，对应的竖直方向梯度为:

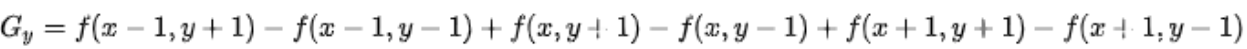
输出梯度图在(x,y)的灰度值为:

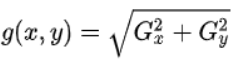
优点：Prewitt算子引入了类似局部平均的运算，对噪声具有平滑作用，较Roberts算子更能抑制噪声。

2.3.3 Sobel算子

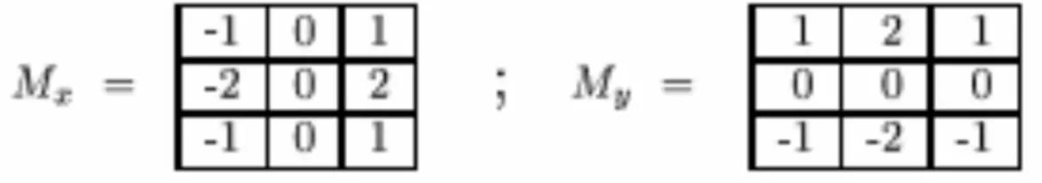
Sobel算子其实就是是增加了权重系数的Prewitt算子，其模板中心对应要求梯度的原图像坐标，对应的8-邻域的像素灰度值如下表所示：

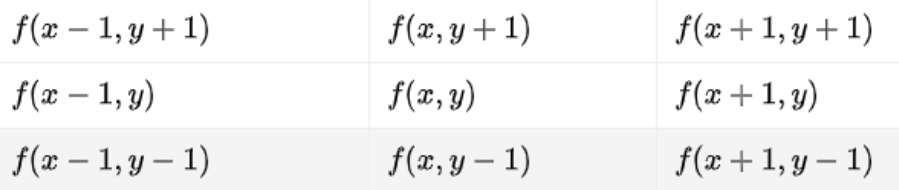
通过Sobel算子的水平模板M(x)卷积后，对应的水平方向梯度为：

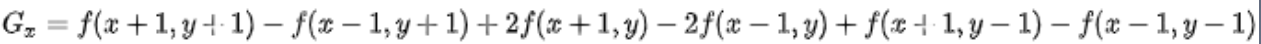
通过Sobel算子的竖直模板M(y)卷积后，对应的竖直方向梯度为:

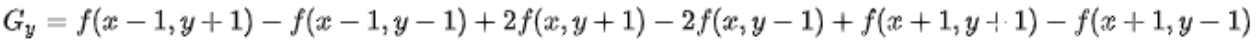
输出梯度图在(x,y)的灰度值为:

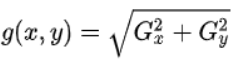
优点：Sobel算子引入了类似局部加权平均的运算，对边缘的定位比要比Prewitt算子好。

因为Sobel算子的效果较好，实际使用中相比于另外两种更多，所以我们只看一下Sobel算子的例子。

函数：

dst	= cv2.Sobel( src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]] )

参数：

1. src：输入图像。

2. ddepth：输出图像位深度，-1表示采用的是与原图像相同的深度。目标图像的深度必须大于等于原图像的深度；

3. dx：x导数的阶数，0表示这个方向上没有求导，一般为0、 1、 2；

4. dy：y导数的阶数，0表示这个方向上没有求导，一般为0、 1、 2；

5. ksize：Sobel算子的尺寸，必须是1，3，5或7。还可以是一个特殊值，ksize = FILTER_SCHARR (-1)，那么将会使用scharr算子，在x方向的算子为：
   在y方向上是这个算子的转置。

6. scale：（可选）计算的导数值的比例因子；默认情况下，不应用缩放。

7. delta：（可选）在将结果存储到dst中之前添加到结果中的增量值。

看个例子：

import numpy as np
import cv2
from matplotlib import pyplot as plt
img = cv2.imread('./image/girl2.png', 0)
sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5)
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=5)plt.subplot(1, 3, 1), plt.imshow(img, cmap = 'gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 3, 2), plt.imshow(sobelx, cmap = 'gray')
plt.title('Sobel X'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 3, 3),plt.imshow(sobely, cmap = 'gray')
plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])
plt.show()

得到的就是该图像在x方向上和y方向上的梯度图：

从这个效果中我们也可以看出，梯度图能够突出图像中的边缘或明暗变化剧烈的地方。

三、Canny边缘检测算法（代码实现）

Canny算法是先平滑后求导数的方法。 John Canny研究了最优边缘检测方法所需的特性，给出了评价边缘检测性能优劣的三个指标：

1. 好的信噪比，即将非边缘点判定为边缘点的概率要低，将边缘点判为非边缘点的概率要低；
2. 高的定位性能，即检测出的边缘点要尽可能在实际边缘的中心；
3. 对单一边缘仅有唯一响应，即单个边缘产生多个响应的概率要低，并且虚假响应边缘应该得到最大抑制。

步骤：

1. 彩色图像转换为灰度图像（以灰度图单通道图读入）
2. 对图像进行高斯模糊（去噪）
3. 计算图像梯度（这里用到了Sobel算子来计算图像梯度），根据梯度计算图像边缘幅值与角度
4. 沿梯度方向进行非极大值抑制（边缘细化）
5. 双阈值边缘连接处理
6. 二值化图像输出结果

在OpenCV中的函数为：

edges =	cv2.Canny( image, threshold1, threshold2[, edges[, apertureSize[, L2gradient]]] )

参数：

1. image：输入图像，灰度图。
2. threshold1：双阈值边缘连接处理的第一个阈值。
3. threshold2：双阈值边缘连接处理的第二个阈值。
4. apertureSize：Sobel算子的尺寸。
5. L2gradient：是否使用L2正则化更精确地计算梯度，还是使用L1。

看个例子：

# 加载 opencv 和 numpy
import cv2
import numpy as np
# 以灰度图形式读入图像
img = cv2.imread('./image/canny.png', 0)
v1 = cv2.Canny(img, 80, 150, (3, 3))
v2 = cv2.Canny(img, 50, 100, (5, 5))# np.vstack():在竖直方向上堆叠
# np.hstack():在水平方向上平铺堆叠
ret = np.hstack((v1, v2))
cv2.imshow('img', ret)
cv2.waitKey(0)
cv2.destroyAllWindows()

原图如下所示：

通过canny检测得到该图的边缘信息，设置了两组参数，得到的结果分别为：

不同的参数设置可能得到不同的结果，很明显第一种参数使得检测得到的边缘信息更少更干净，而第二种得到的更多更全面，实际使用中可以自己调节。

Canny检测作为传统的图像边缘提取算法，虽然效果上不如现在大火的深度学习的各种网络，但是对于一些边缘信息较为明显单一的图像来说任然有使用价值，我们将输入图像换一下：

再用Canny检测（上述代码，换一下输入图像即可），得到的结果为：

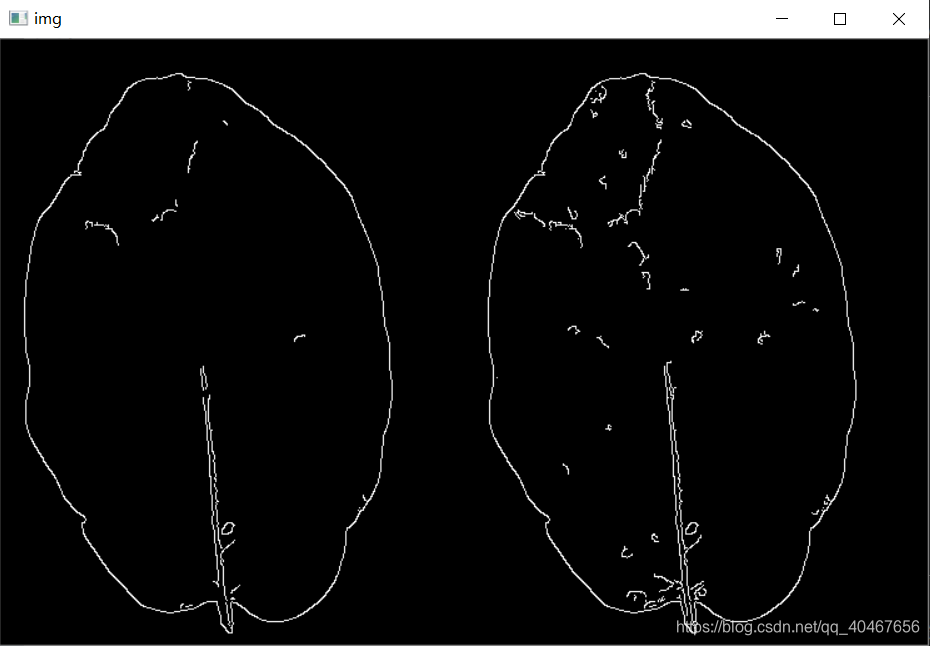
可以看到检测效果已经非常不错了，更重要的是，它不需要训练，所以速度非常的快，这是它很大的一个优点，所以现在还是会使用到Canny检测。