12月3日，陶哲轩在其个人博客上更新了一篇文章，

https://terrytao.wordpress.com/2019/12/03/eigenvectors-from-eigenvalues-a-survey-of-a-basic-identity-in-linear-algebra/

说他与合作者在arXiv上更新了此前关于特征值的文章

Eigenvectors from Eigenvalues。

更新后，陶哲轩等将文章题目改为

Eigenvectors from Eigenvalues: 

a survey of a basic identity in linear algebra

即注明这篇文章是一篇综述。

arxiv.org/abs/1908.03795

文章的要点是一个特征向量-特征值等式。

熟悉背景的网友们知道(参考关于陶哲轩《来自特征值的特征向量》)，8月10日，陶哲轩与合作者在线发表了一篇文章。合作起因也很传奇，是物理学家发现了一个简单而神奇的公式，即特征向量-特征值等式，请教陶哲轩，于是合作了文章(参考陶哲轩为之惊叹的最新公式)。这个公式的特点是很简单自然，但很少见。

文章发表后，11月份quanta发表文章对这个故事进行介绍(中文翻译文章也出来，引起了很大反响)而广为人知。美国华人丁教授还写了篇文章《与陶哲轩“共舞”的一个周末 | 数学家发现纪实》。

作者们也因此获得了许多反馈。

中文世界的故事可以用一些人喜欢的“反转”来描述。因为有人很快发现这个结论其实很早前就有了，特别是北大一位教授所著中文书中也有。有人因此批评陶哲轩作为著名数学家，所得到的发现只不过是很早前就有人发现过了的，做出“大神不过尔尔”的评论。

现在陶哲轩等人经过与人(在线讨论、私下交流、文献引用等)交流研究，发现这个公式在数值线性代数、随机矩阵、图论等各个领域常被证明，也常被遗忘。此前人们一般认为这个公式最早出自1968的一篇文章。现在陶哲轩等研究发现最早的相关文献可以追溯到1934年。后来不断有证明，陶哲轩本人自己也用过相关公式。

下面是陶哲轩自己在其博客中关于这个故事的叙述，并且给出了一个树图——文献中证明、引用该等式的历史。

When we posted the first version of this paper, we were unaware of previous appearances of this identity in the literature; a related identity had been used by Erdos-Schlein-Yau and by myself and Van Vu for applications to random matrix theory, but to our knowledge this specific identity appeared to be new. Even two months after our preprint first appeared on the arXiv in August, we had only learned of one other place in the literature where the identity showed up (by Forrester and Zhang, who also cite an earlier paper of Baryshnikov).

The situation changed rather dramatically with the publication of a popular science article in Quanta on this identity in November, which gave this result significantly more exposure. Within a few weeks we became informed (through private communication, online discussion, and exploration of the citation tree around the references we were alerted to) of over three dozen places where the identity, or some other closely related identity, had previously appeared in the literature, in such areas as numerical linear algebra, various aspects of graph theory (graph reconstruction, chemical graph theory, and walks on graphs), inverse eigenvalue problems, random matrix theory, and neutrino physics. As a consequence, we have decided to completely rewrite our article in order to collate this crowdsourced information, and survey the history of this identity, all the known proofs (we collect seven distinct ways to prove the identity (or generalisations thereof)), and all the applications of it that we are currently aware of. The citation graph of the literature that this ad hoc crowdsourcing effort produced is only very weakly connected, which we found surprising:

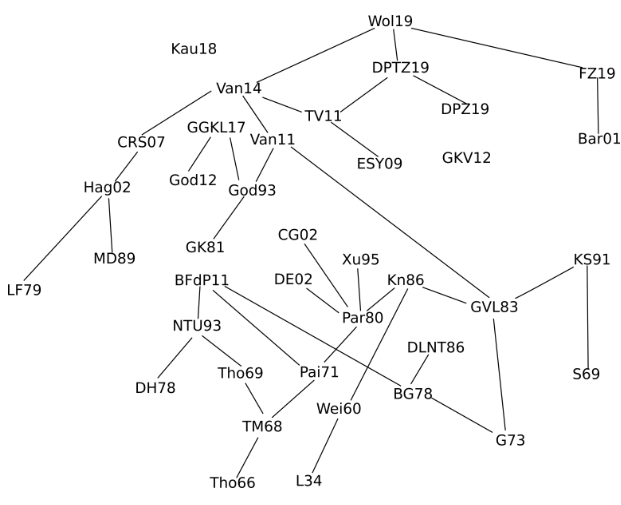
The earliest explicit appearance of the eigenvector-eigenvalue identity we are now aware of is in a 1966 paper of Thompson, although this paper is only cited (directly or indirectly) by a fraction of the known literature, and also there is a precursor identity of Löwner from 1934 that can be shown to imply the identity as a limiting case. At the end of the paper we speculate on some possible reasons why this identity only achieved a modest amount of recognition and dissemination prior to the November 2019 Quanta article.

陶哲轩等人的文章介绍了相关背景，给出了7个不同的证明。相信这个优美的公式将来不会再被遗忘。陶哲轩与特征值特征向量等式的故事完美地描述了一个数学家做研究的历程。非常令人喜欢。

数学结果被忘记被再次发现，是常见现象。陶哲轩等人先前不知道这个结果的存在，不必苛责。这使得我们想起一位学生的问题：很多中学几何题可以用解析代数的办法求解，还用几何方法有意义吗？实际上，不同的证明给出了不同的理解。例如，陶哲轩等人的再研究让我们对这个等式有了新的认识。