文章目录
- 1.预备知识
- 1.1 递归
- 1.2 回溯
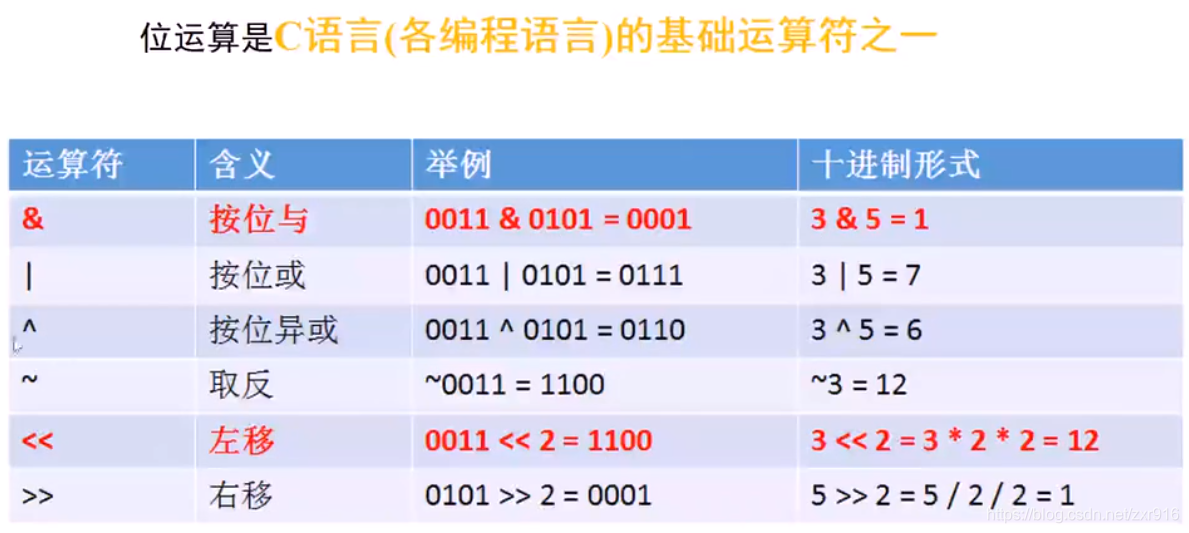
- 1.3 位运算
- 2.子集
- 2.1 题目描述
- 2.2 解题思路——回溯递归法
- 2.3 C++实现
- 2.4 解题思路——位运算法
- 2.5 位运算实现
- 3.子集 II
- 3.1 题目描述
- 3.2 解题思路
- 3.3 回溯递归法——C++实现
- 3.4 位运算——C++实现
- 4.组合总和 II
- 4.1 题目描述
- 4.2 解题思路
- 4.3 C++实现
- 5.括号生成
- 5.1 题目描述
- 5.2 解题思路
- 5.3 C++实现
- 6.N 皇后
- 6.1 题目描述
- 6.2 棋盘和皇后表示
- 6.3 回溯算法
- 6.4 C++实现
- 7.
- 7.1 预备知识
- 7.2 题目描述
- 7.3 C++实现
1.预备知识
1.1 递归

1.2 回溯
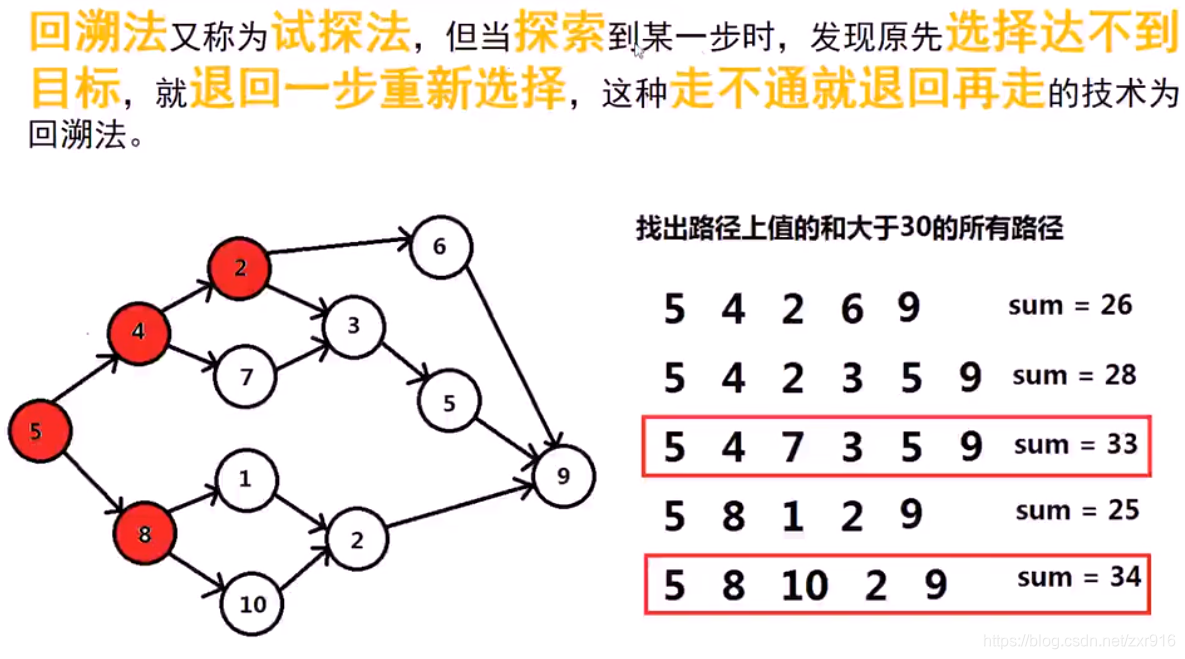
1.3 位运算
2.子集
2.1 题目描述
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集
2.2 解题思路——回溯递归法
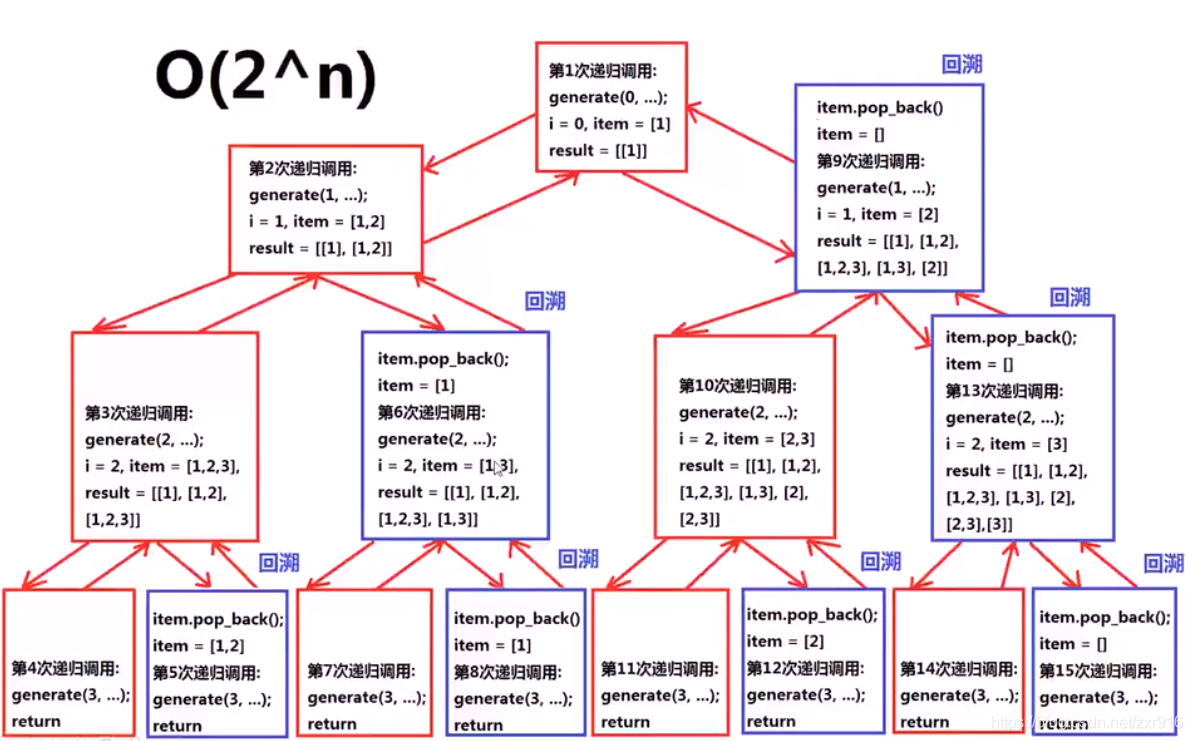
2.3 C++实现
class Solution {
public:vector<vector<int>> subsets(vector<int>& nums) {vector<int> item;vector<vector<int>> result;result.push_back(item);generate(0,nums,item,result);return result;}
private:void generate(int i,vector<int>& nums,vector<int>& item,vector<vector<int>>& result){if(i>=nums.size()){return;}item.push_back(nums[i]);result.push_back(item);generate(i+1,nums,item,result);item.pop_back();generate(i+1,nums,item,result);}
};
2.4 解题思路——位运算法
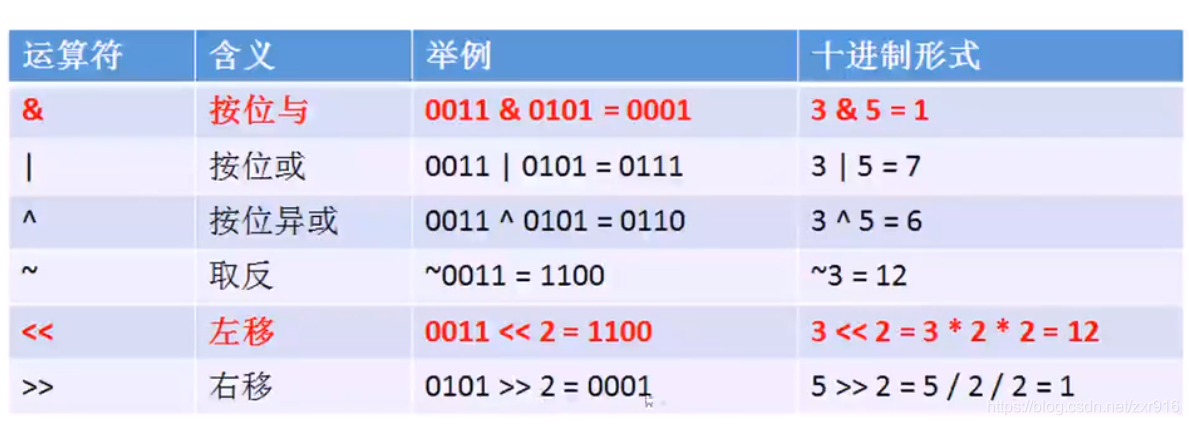
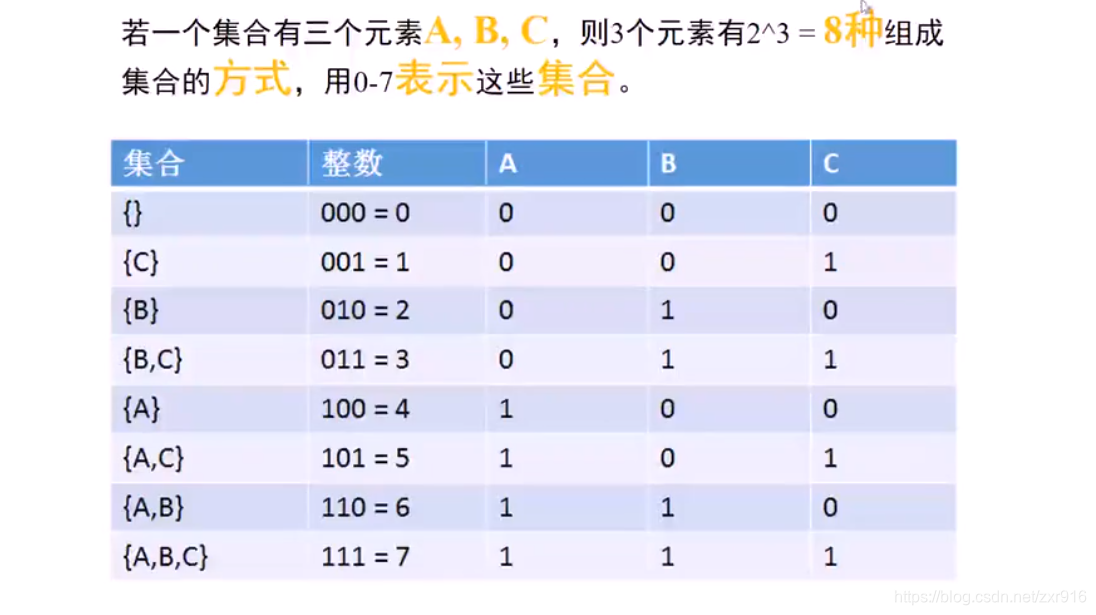
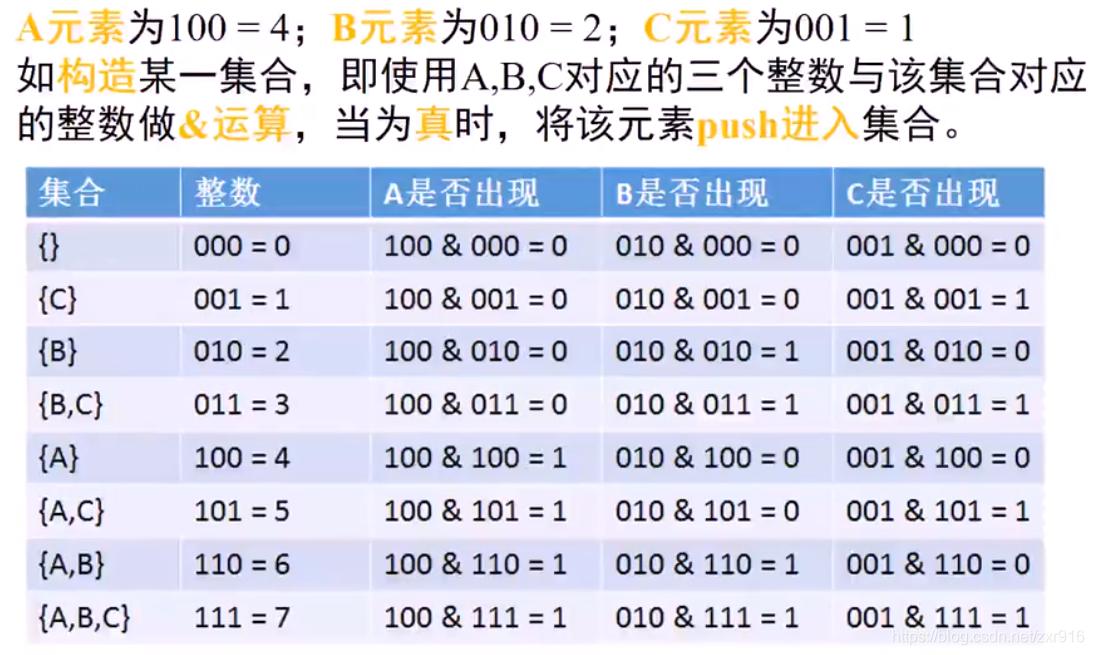
2.5 位运算实现
class Solution {
public:vector<vector<int>> subsets(vector<int>& nums) {vector<vector<int>> result;//int all_set=pow(2,nums.size());int all_set=1<<nums.size();for(int i=0;i<all_set;i++){vector<int> item;for(int j=0;j<nums.size();j++){if(i&(1<<j)){item.push_back(nums[j]);}}result.push_back(item);}return result;}};
3.子集 II
3.1 题目描述
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
3.2 解题思路


3.3 回溯递归法——C++实现
class Solution {
public:vector<vector<int>> subsetsWithDup(vector<int>& nums) {vector<int> item;vector<vector<int>> result;set<vector<int>> res_set;sort(nums.begin(),nums.end());result.push_back(item);generate(0,nums,item,result,res_set);return result;}
private:void generate(int i,vector<int>& nums,vector<int>& item,vector<vector<int>>& result,set<vector<int>>& res_set){if(i>=nums.size()){return;}item.push_back(nums[i]);if(res_set.find(item)==res_set.end()){result.push_back(item);res_set.insert(item);}generate(i+1,nums,item,result,res_set);item.pop_back();generate(i+1,nums,item,result,res_set);}
};
3.4 位运算——C++实现
class Solution {
public:vector<vector<int>> subsetsWithDup(vector<int>& nums) {int all_set;vector<vector<int>> result;set<vector<int>> res_set;sort(nums.begin(),nums.end());all_set=1<<nums.size();for(int i=0;i<all_set;i++){vector<int> item;for(int j=0;j<nums.size();j++){if(i&(1<<j)){item.push_back(nums[j]);}}if(res_set.find(item)==res_set.end()){result.push_back(item);res_set.insert(item); }}return result;}
};
4.组合总和 II
4.1 题目描述
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
4.2 解题思路
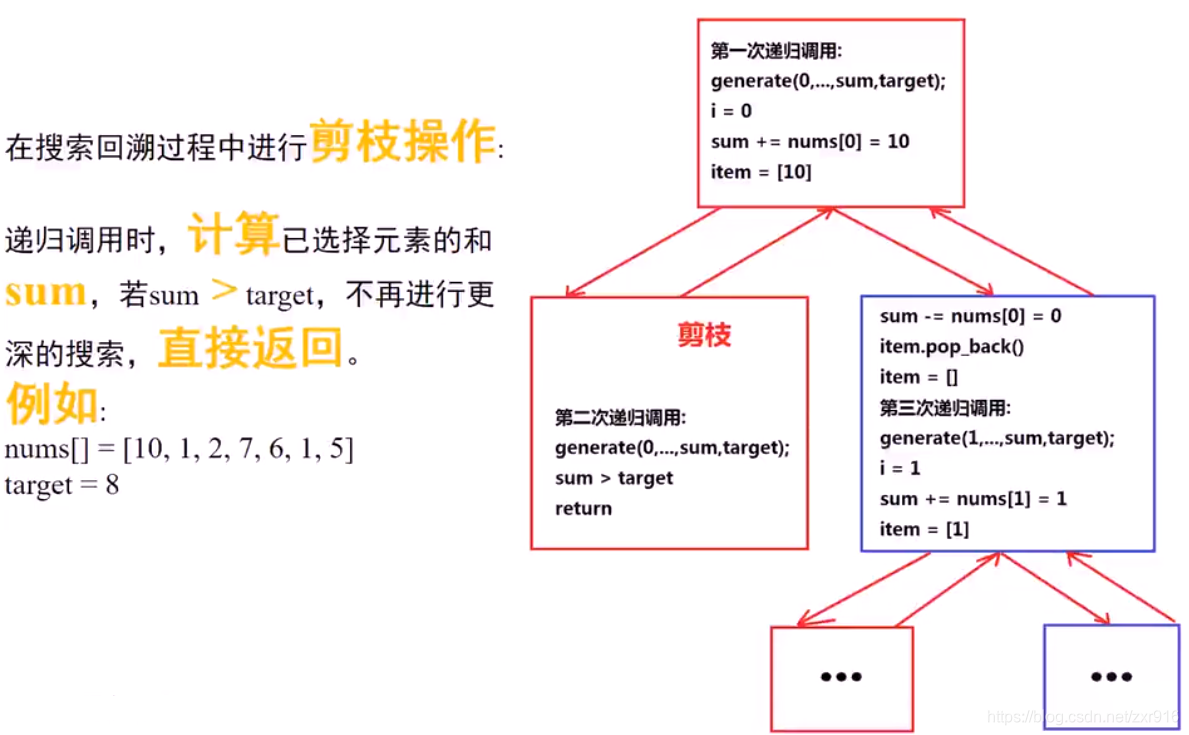
4.3 C++实现
class Solution {
public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<int> item;vector<vector<int>> result;set<vector<int>> res_set;sort(candidates.begin(),candidates.end());generate(0,candidates,item,result,res_set,0,target);return result;}
private:void generate(int i,vector<int>& candidates,vector<int>& item,vector<vector<int>>& result,set<vector<int>>& res_set,int sum, int target){if(i>=candidates.size()||sum>target){return;}sum+=candidates[i];item.push_back(candidates[i]);if(sum==target&&res_set.find(item)==res_set.end()){result.push_back(item);res_set.insert(item);}generate(i+1,candidates,item,result,res_set,sum,target);sum-=candidates[i];item.pop_back();generate(i+1,candidates,item,result,res_set,sum,target);}
};
5.括号生成
5.1 题目描述
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
5.2 解题思路


5.3 C++实现
class Solution {
public:vector<string> generateParenthesis(int n) {vector<string> result;generate("",n,n,result);return result;}
private:void generate(string item,int left,int right,vector<string>& result){if(left==0&&right==0){result.push_back(item);return;}if(left>0){generate(item+'(',left-1,right,result);}if(left<right){generate(item+')',left,right-1,result);}}
};
6.N 皇后
6.1 题目描述
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
1 <= n <= 9
皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
6.2 棋盘和皇后表示


6.3 回溯算法
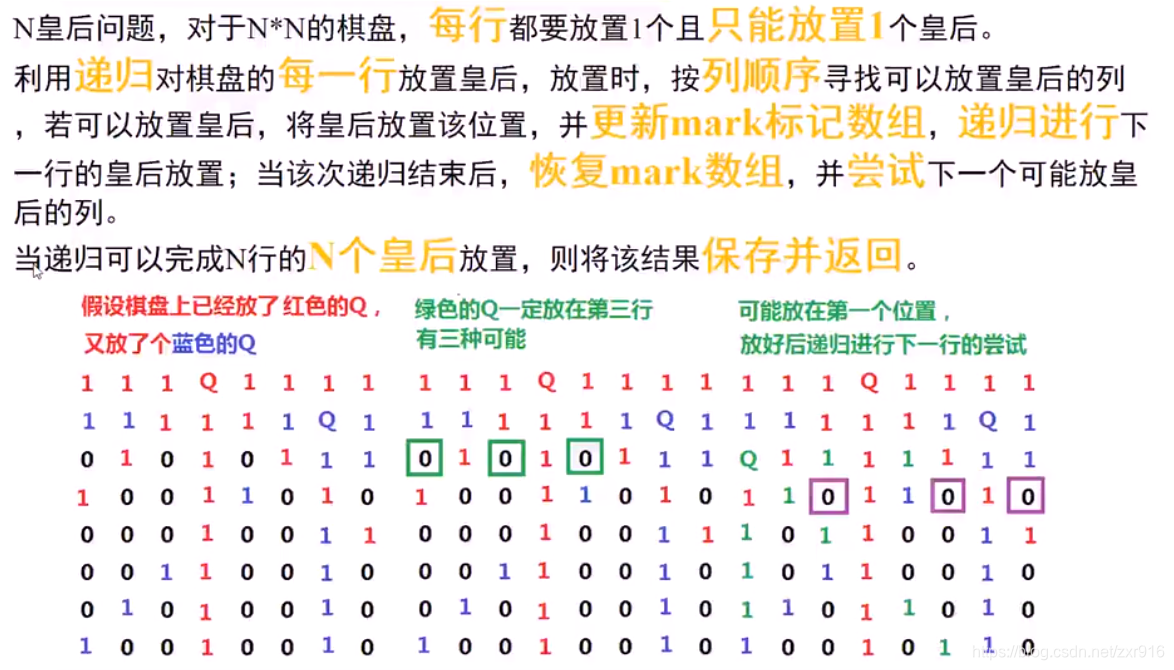
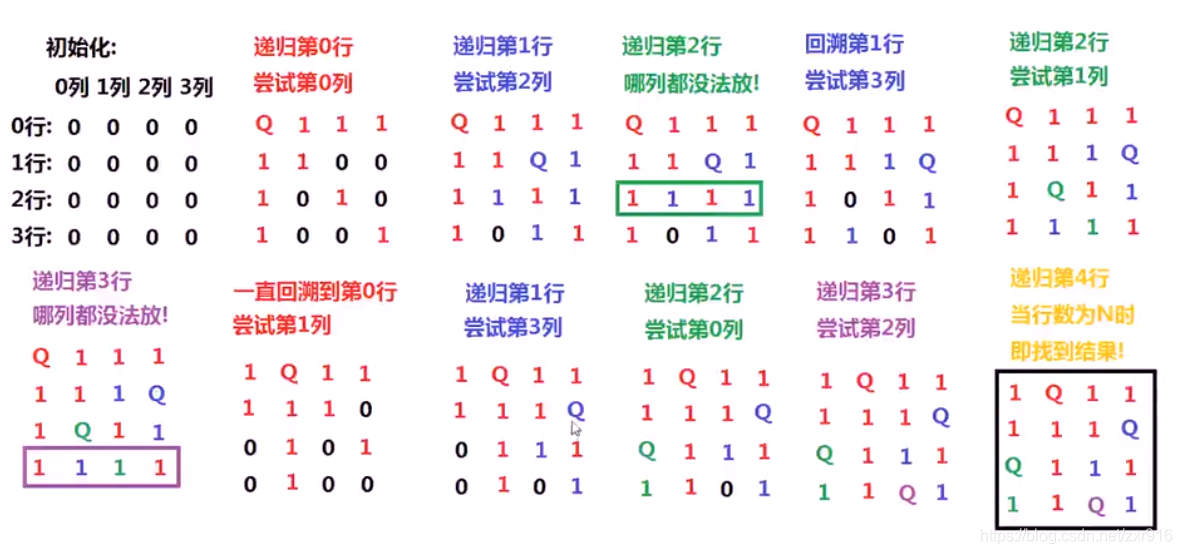
6.4 C++实现
class Solution {
public:vector<vector<string>> solveNQueens(int n) {vector<vector<string>> result;vector<vector<int>> mark;vector<string> location;for(int i=0;i<n;i++){mark.push_back((vector<int>()));for(int j=0;j<n;j++){mark[i].push_back(0);}location.push_back("");location[i].append(n,'.');}generate(0,n,location,result,mark);return result;}
private:void put_down_the_queen(int x,int y,vector<vector<int>>&mark){static const int dx[]={-1,1,0,0,-1,-1,1,1};static const int dy[]={0,0,-1,1,-1,1,-1,1};mark[x][y]=1;int new_x,new_y;for(int i=1;i<mark.size();i++){for(int j=0;j<8;j++){new_x=x+i*dx[j];new_y=y+i*dy[j];if(new_x>=0&&new_x<mark.size()&&new_y>=0&&new_y<mark.size()){mark[new_x][new_y]=1;}}}}void generate(int k,int n,vector<string> &location,vector<vector<string>> &result,vector<vector<int>> &mark){if(k==n){result.push_back(location);return;}for(int i=0;i<n;i++){if(mark[k][i]==0){vector<vector<int>> tmp_mark=mark;location[k][i]='Q';put_down_the_queen(k,i,mark);generate(k+1,n,location,result,mark);mark=tmp_mark;location[k][i]='.';}}}
};
7.
7.1 预备知识
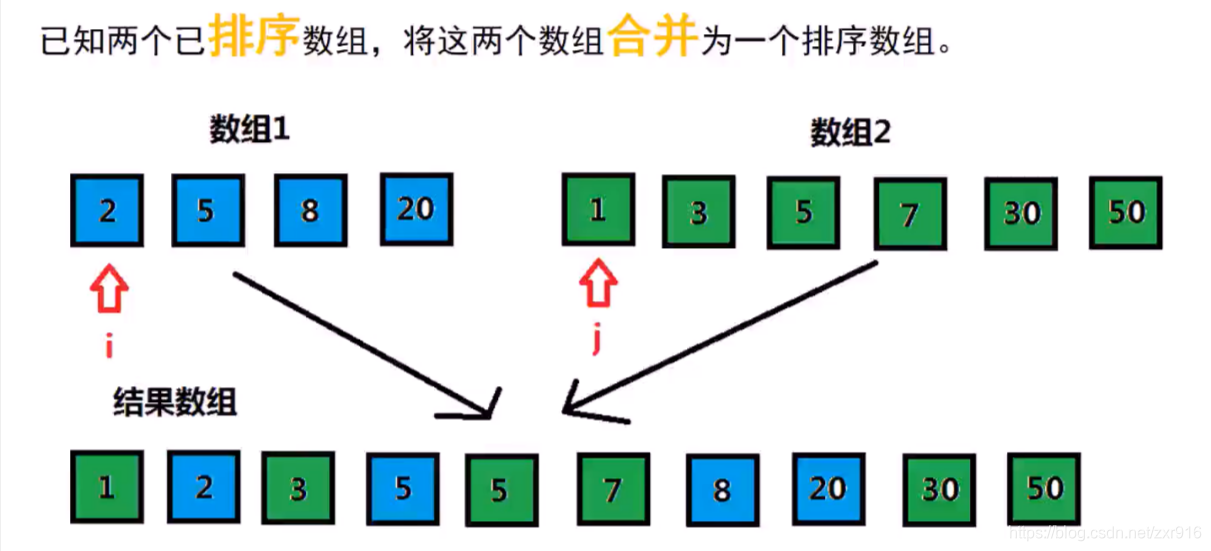
#include<vector>void merge_sort_two_vec(vector<int> &sub_vec1,vector<int> &sub_vec2,vector<int> &vec){int i=0,j=0;while(i<sub_vec1.size()&&j<sub_vec2.size()){if(sub_vec1[i]<=sub_vec2[j]){vec.push_back(sub_vec1[i]);i++;} else{vec.push_back(sub_vec2[j]);j++;} } for(;i<sub_vec1.size();i++){vec.push_back(sub_vec1[i]);} for(;j<sub_vec2.size();j++){vec.push_back(sub_vec2[j]);} }
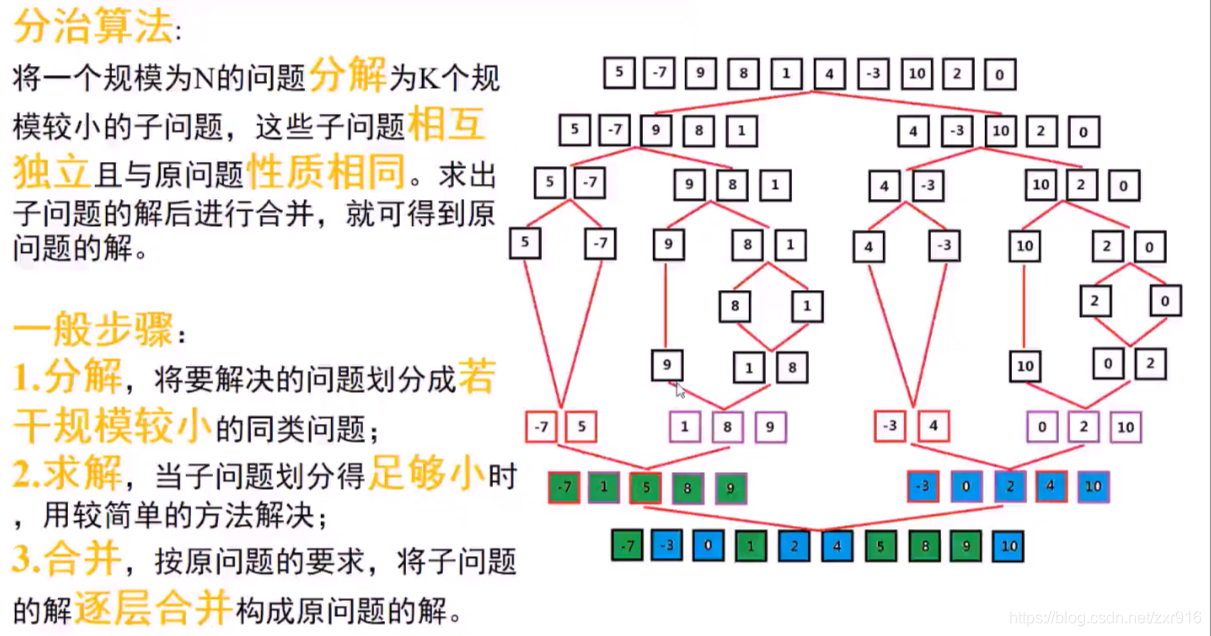
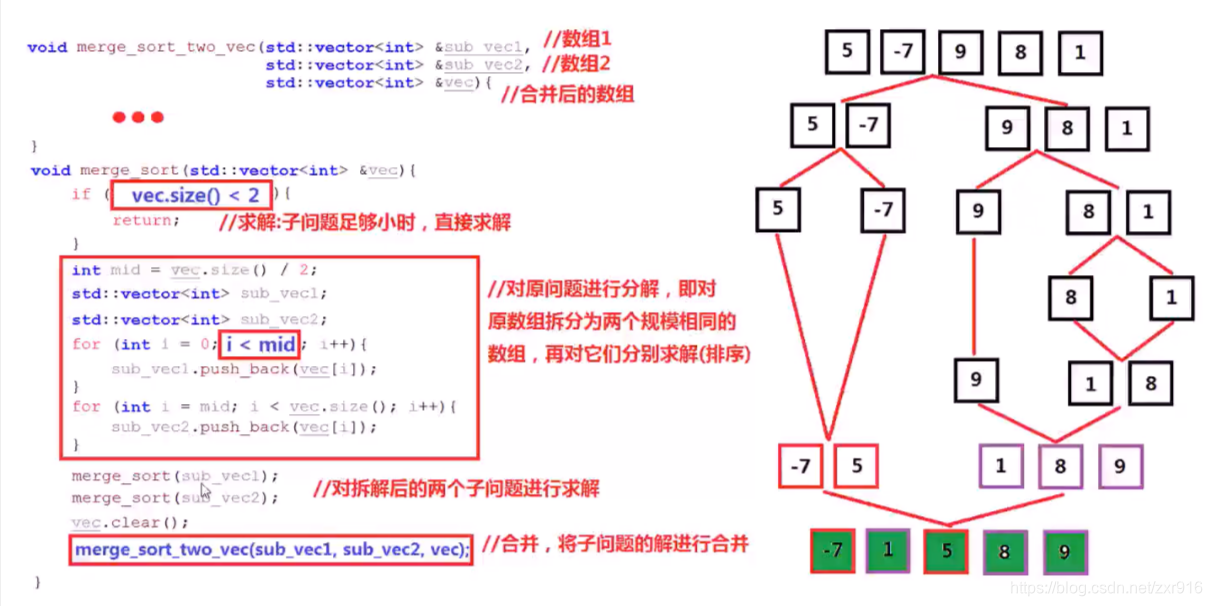
7.2 题目描述
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
7.3 C++实现
代码实现



:await返回Task的async方法)



群体合作行为的演化)











