Wasserstein metric的通俗解释

关注他

166 人赞同了该文章

本文收录在无痛的机器学习第二季目录。

Wasserstein GAN可以算是GAN界的一大突破了，有关它的介绍和使用心得的文章也已经满天飞了，感兴趣的童鞋随便一搜就能好多，今天就不说太多大家说过的内容，我们从一个十分通俗的角度来看看这个目标函数究竟做了些什么。

一个简单的例子

如果直接去看Wasserstein metric的定义，相信对实变函数、泛函分析、测度论等数学学科不熟悉的人来说简直是云里雾里：

$W(\mu, \upsilon)=\inf_{\gamma \in \Gamma (\mu, \upsilon)} \int_{M \times M}d(x,y) d \gamma(x,y)$

这公式都说了些什么，看到就头疼，看看旁边的解释，稍微明白一点，但还是晕晕乎乎的。下面我们就从一个简单的例子开始说起，然后慢慢过渡到这个公式上来。

我们使用最优运输里面的一个小例子，假设我国的某市要修建立交桥，修高速公路需要石头，现在已经查明城市附近有几个山头有石头，我们希望把石头采集来并运输到立交桥的几个建造地点，如图所示：

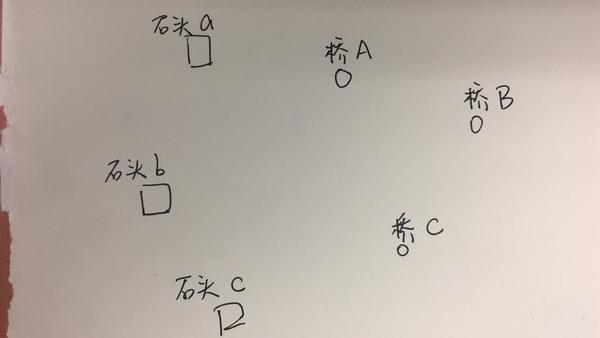
我们假设其他的工作都没有花费，只有运输这一步花费，那么从这些石头产生地把石头运到建桥处，怎么最省钱呢？

为了计算方便，我们需要再做一些设定：

石头a处有100单位石头
石头b处有50单位石头
石头c处有100单位石头
桥A处需要100单位石头
桥B处需要50单位石头
桥C处需要100单位石头

各个点的距离如下所示：

d(a,A)=10, d(a,B)=20, d(a,C)=30
d(b,A)=25, d(b,B)=25, d(b,C)=25
d(c,A)=20, d(c,B)=30, d(c,C)=10

我们假设每搬运1单位石头行走1单位距离，我们要花费1块钱，那么最优的搬运路径是什么，怎么最省钱？

这个问题其实也不算很复杂，我们令x[s][t]表示把s石头处运往t桥处的石头数量，那么就有下面的公式：

min 10*x[a][A]+20*x[a][B]+30*x[a][C]+25*x[b][A]+25*x[b][B]+25*x[b][C]+20*x[c][A]+30*x[c][B]+10*x[c][C]
s.t.
# 石头的约束
x[a][A]+x[a][B]+x[a][C]=100
x[b][A]+x[b][B]+x[b][C]=50
x[c][A]+x[c][B]+x[c][C]=100
# 桥的约束
x[a][A]+x[b][A]+x[c][A]=100
x[a][B]+x[b][B]+x[c][B]=50
x[a][C]+x[b][C]+x[c][C]=100

那么这个问题能不能求出最优解呢？当然可以，这道线性规划的问题就交给感兴趣的童鞋自行研究答案了。总之我们列出了公式，并给明了对应的约束条件，大家对这个问题应该已经十分清晰了。

不过话说回来，这个问题和Wasserstein有关系么？当然有。我们需要对上面的公式做一些抽象了。

首先是最小化的函数，我们用 $d(s,t)$ 表示石头到桥的距离，用 $m(s,t)$ 表示运输石头的数量，这样目标函数就变成了：

$min \sum_{\pi(s,t)}d(s,t)*m(s,t)$

其中的 $\pi$ 表示了s,t的所有组合形式，这个问题下，我们有9种组合形式。

然后就是下面的约束内容了，我们再定义 $s(x)$ 表示石头处拥有石头的数量， $t(x)$ 表示桥需要的石头数量，那么就有

$\sum_t m(s,t)=s(s), \forall s$

$\sum_s m(s,t)=t(t),\forall t$

怎么样，和上面的公式是不是靠近了不少？

升级版问题

下面我们要把问题升级一下，前面的数字都是几百几百的，和我们想要的公式不太一样，我们能不能把它们归一化一下，也就是说，把每个数字都除以它们的总和？

这样就有：

石头a有0.4的石头（100/250）
石头b有0.2的石头

……

桥A需要0.4的石头（100/250）

……

这样带来一个好处，我们发现它从数值上和概率值很像了：

首先这些值非0
其次它们的加和为1
当然还满足一些我们一般不关注的性质（次可数可加性）

嗯，专业来说这个就可以想象成概率测度函数了，我们完成了一个关键的变化，此时我们需要变换一下符号：

s(s)变成 $\mu(s)$ ，表示对所有石头的“概率测度”，它的空间是a,b,c三处的石头

t(t)变成 $\upsilon(t)$ ，表示对所头桥的“概率测度”，它的空间是A,B,C三处的桥

那么m(s,t)呢？看上去和我们学过的联合概率很像嘛，当然这里我们学术一点，管它叫积空间 $\Gamma$ ，积空间上的“概率测度”函数就是之前的m(s,t)，我们现在管它叫 $\gamma(s,t)$

好了，到这里，我们可以再看看我们对问题的描述了：

$min_{\gamma(s,t)} \sum_{(s,t) \in \Gamma} \gamma(s,t) * d(s,t)$

s.t.

$\sum_t\gamma(s,t)=\mu(s),\forall s$

$\sum_s \gamma(s,t)=\upsilon(t),\forall t$

嗯，感觉离最终想要的目标不远了。我们还发现了一个现象，如果把 $\gamma$ 想象成一个联合分布，那么它的两个边缘分布分别就是 $\mu(s)$ 和 $\upsilon(t)$ ，这样两个约束条件也可以用一句话来描述了。

升级2.0的问题

下面完成问题解释的最后一步，前面看到的问题都是离散问题，我们能不能把它表示成连续的问题？我们有一片石头上，每一处都有若干的石头，我们有一片区域都要建桥，每个点上都可能需要石头，于是前面提到的 $\mu(s)$ 、 $\upsilon(t)$ 和 $\gamma(s,t)$ 全部变成了连续分布，于是问题又变成了：

$min_{\gamma(s,t)} \int_{\Gamma}d(s,t)d\gamma(s,t)$