Introduction

原型网络的思路非常简单：对于分类问题，原型网络将其看做在语义空间中寻找每一类的原型中心。

原型中心：针对Few-shot的任务定义，原型网络训练时学习如何拟合中心。学习一个度量函数，该度量函数可以通过少量的几个样本找到所属类别在该度量空间的原型中心。

聚类中心：测试时，用支持集（Support Set）中的样本来计算新的类别的聚类中心，再利用最近邻分类器的思路进行预测。

本文主要针对Few-Show／Zero-Shot任务中过拟合的问题进行研究，将原型网络和聚类联系起来，和目前的一些方法进行比较，取得了不错的效果。

Related Work

本文主要提及了两类Few-Shot方法：

1. 匹配网络（Matching Network）：

可以理解为在embedding空间中的加权最近邻分类器。

模型在训练过程中通过对类标签和样本的二次采样来模仿Few-Shot任务的测试场景，学习一个匹配网络。

该网络只在训练集中的关系基础上训练，并且直接应用于测试集中的关系。原型网络也属于一种匹配网络。

2. Optimization-based meta-learning：

这种方法在训练的过程中的目标是学习如何通过少量样本更好的拟合数据，因此该类方法会针对测试数据集对网络进行调整。

例如，在训练过程中，利用LSTM的网络结构学习每个训练step所需要的学习率。

Model

在这里插入图片描述

每一个类的原型 $c_k$ 是支持集中的样本embedding的均值向量，其中 $S_k$ 为支持集中每个类的样本：
在这里插入图片描述

计算query instance和各个类原型间的距离，通过softmax得到分类概率分布：
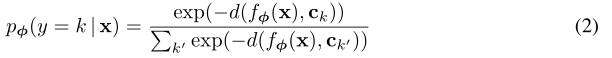
在这里插入图片描述

在训练时，作者结合episodes和mini-batch的思路模拟测试场景进行训练，伪代码如下：

接下来作者从几个角度对模型进行了理论上的分析：

原型网络的学习过程可以理解为混合概率估计。
对于距离的度量属于Bregman散度（https://www.zhihu.com/question/22426561/answer/209945856），其中就包括平方欧氏距离和Mahalanobis距离。

该文中正是利用了平方欧氏距离。在此距离度量的基础上，在support set上利用向量均值（文中公式1）所找到的则为最优的聚类中心。
将原型网络重新解释为线性模型，对应用欧式距离进行了分析。

在应用欧式距离时，上文的softmax相当于有特定参数的线性模型，带入

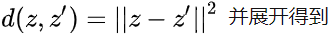
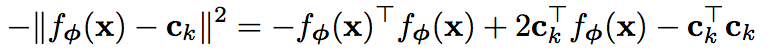
第一项相对于k来说是常量，不影响softmax的概率结果，对后两项展开写成线性形式：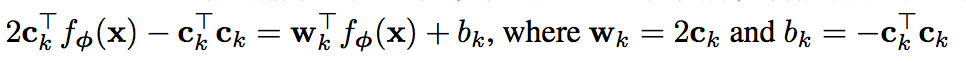

作者猜想embedding function内部已经学到了所需的非线性元素，使用欧式距离使得方法更加简单有效。
特别与匹配网络进行了比较

这两种方法在One-Shot情况下是等价的，匹配网络在给定支持集的情况下生成一个加权最近邻分类器；原型网络使用欧式距离生成一个线性分类器。

当支持集中每个类只有一个样本的时候， $c_k=x_k$ , 二者等价。目前的匹配网络有相对复杂的结构，比如去耦支持样本和qurey样本的embedding函数、用FCE等等，可以融合到原型网络中，但是却增加了参数。本文证明用简单的设计也能达到相当的效果
思考如果每个类的原型数目不是一个而是多个，则需要对支持集中样本额外分区。目前的方法都需要一个额外的分区阶段，和权重更新过程是相互独立的。而本文提出的方法只需要用简单的梯度下降方法去学习
Zero-Shot:

对于零样本学习任务，每个类的原型可以是事先知道的元数据向量 $v_k$ ，也可以通过学习来得到，（之前有研究通过纯文本来学习）。

这个时候class embedding和query embedding样本来自不同域，作者发现可用固定原型embedding的长度为单位长度，对query embedding不限制。