LeetCode 802. 找到最终的安全状态（逆向图+拓扑排序）

文章目录

- 1. 题目
- 2. 解题

1. 题目

在有向图中, 我们从某个节点和每个转向处开始, 沿着图的有向边走。
如果我们到达的节点是终点 (即它没有连出的有向边), 我们停止。

现在, 如果我们最后能走到终点，那么我们的起始节点是最终安全的。
更具体地说, 存在一个自然数 K, 无论选择从哪里开始行走, 我们走了不到 K 步后必能停止在一个终点。

哪些节点最终是安全的？结果返回一个有序的数组。

该有向图有 N 个节点，标签为 0, 1, …, N-1, 其中 N 是 graph 的节点数.
图以以下的形式给出: graph[i] 是节点 j 的一个列表，满足 (i, j) 是图的一条有向边。

示例：
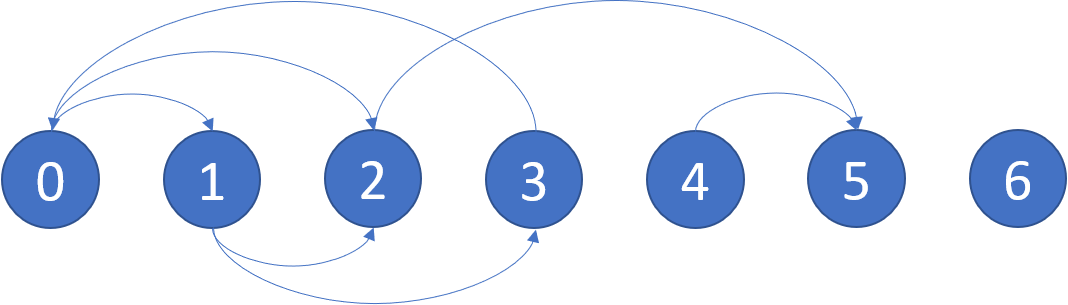
输入：graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出：[2,4,5,6]
这里是上图的示意图。

在这里插入图片描述

提示：
graph 节点数不超过 10000.
图的边数不会超过 32000.
每个 graph[i] 被排序为不同的整数列表， 在区间 [0, graph.length - 1] 中选取。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-eventual-safe-states
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

建立逆向图
拓扑排序，出度为0的入队

class Solution {
public:vector<int> eventualSafeNodes(vector<vector<int>>& graph) {int n = graph.size();vector<int> outdegree(n, 0);//出度vector<int> ans;queue<int> q;for(int i = 0; i < n; i++) {outdegree[i] = graph[i].size();if(outdegree[i]==0)//出度为0的是可以到达的终点q.push(i);}vector<vector<int>> rg(n);for(int i = 0; i < n; i++){for(int j : graph[i])rg[j].push_back(i);//建立逆向图}while(!q.empty()){int id = q.front();q.pop();for(auto nt : rg[id])//逆向图{if(--outdegree[nt] == 0)q.push(nt);}}for(int i = 0; i < n; ++i)if(outdegree[i]==0)ans.push_back(i);return ans;}
};