本文系 KDD2019 论文的解读:
Wang, Jingyuan, Ning Wu, Wayne Xin Zhao, Fanzhang Peng, and Xin Lin. "Empowering A* Search Algorithms with Neural Networks for Personalized Route Recommendation." InProceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 539-547. ACM, 2019.
作者:吴宁
研究动机
A* 算法因为它的高效和准确而被广泛应用于路径发现和图遍历等任务上。斯坦福的 Peter Hart, Nils Nilsson and Bertram Raphael(Nils Nilsson 老先生于 2019 年 4 月 23 日去世,哀悼)于 1968 年首次提出了 A* 算法。A* 算法在寻找最优路径的过程中,使用 f(n) 来评价所有候选节点的得分,每次要扩展结点的时候都会选择那个 f(n) 最小的节点:
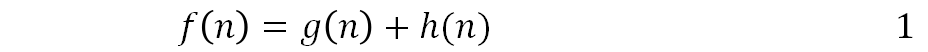
g(n) 是从出发点到 n 节点的费用值,而 h(n) 是一个被估计的从 n 到终点的费用值。不同于Dijkstra算法,A* 算法需要多考虑一个启发值 h(n),通过启发值的帮助,A* 算法可以大大减小搜索空间。
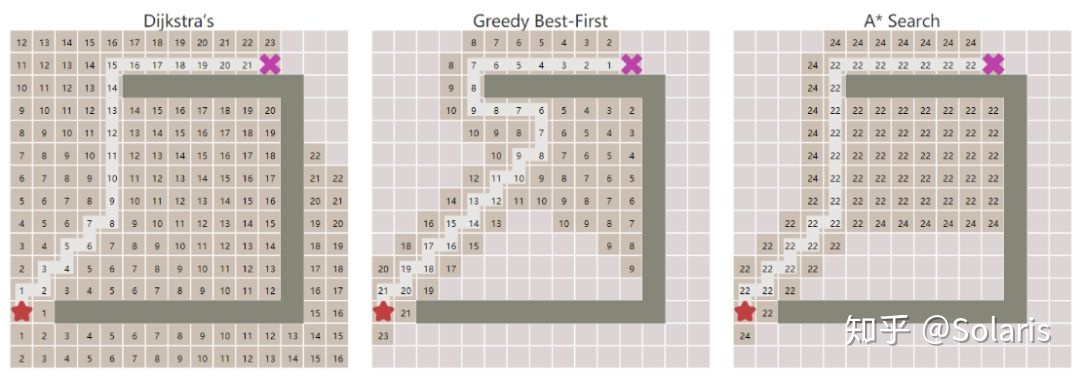
上图是三种搜索算法的对比,Dijkstra 算法只使用 g(n), 虽然可以找到最优路径,但是搜索空间巨大。贪心的最佳优先(Greedy Best-First)算法只使用 h(n),虽然减小了搜索空间,但是不能保证得到最优的结果。而 A* 算法可以保证得到最优路径,并且大大减小了搜索空间。
传统的 A* 算法使用一些比较简单的指标作为 g(n) 和 h(n),比如欧氏距离,用以解决最短路径等比较简单的问题,因此对于一些复杂的非线性问题的搜索求解并不适用。
在智能交通领域,一个非常典型的例子就是个性化的路径推荐。传统的 A* 算法对于“最短路径”、“最快路径”的搜索非常有效,但是对于“最喜欢的路径”搜索就很难发挥作用。
因为用户的偏好是一个非常复杂的非线性过程,无法用简单的欧氏距离进行度量。面对这样的问题,我们提出使用深度神经网络来学习 A* 算法的 g(n) 和 h(n) 值,以此来帮助 A* 算法解决更为复杂的问题。
研究思路
我们以个性化出行路径推荐为例子介绍神经网络是怎样与 A* 算法结合的。出行路径推荐是一个和我们平时生活息息相关的问题,也一直是各大地图应用的核心算法之一。一个好的路径推荐算法,可以提升人们的出行体验,为经济社会的发展带来价值。
出行路径推荐受到了学术界和工业界的广泛关注,最初的路径规划算法讨论的是怎样在路网上找到一条最短路径。随着时代的发展,基于历史轨迹数据的个性化的路径推荐任务也开始受到研究者们的关注。
过去的路径推荐方案大多以 A* 搜索为框架不同的费用函数对应于不同的搜索任务,比如说以移动距离为费用,那么搜索的便是最短路径,以用时为费用,那么搜索的便是最快路径,以用户的偏好为费用,那么便是个性化的路径推荐。
在现有工作中,大家往往以简单的统计或者浅层的模型来作为搜索的费用函数,但是用户的喜好往往是难以被如此简单地建模的,因此,我们提出用神经网络来学习 A* 搜索算法中的费用函数,以此为基础结合 A* 搜索算法来完成个性化的路径推荐。本文 Empowering A ∗ Search Algorithms with Neural Networks for Personalized Route Recommendation 已经被 KDD 2019 收录,可以通过https://arxiv.org/pdf/1907.08489.pdf 下载。
模型介绍
任务定义
路径推荐任务中,我们的模型接受一个历史轨迹数据集D,起点 ls,终点 ld,出发时间 b 和用户 u 作为输入,然后基于输入推荐个性化的轨迹 。形式化地来讲,我们需要找到一条条件概率最高的最优路径:

基于A*算法的解决方案
首先我们讨论传统 A* 算法在路径推荐上的应用。A* 算法是 Dijkstra 算法的扩展,在寻找最优路径的过程中,它每次扩展一个结点 n,然后使用 f(n) 来评价这个节点的得分:

g(n) 是从出发点到 n 节点的费用值,而 h(n) 是一个被估计的从 n 到终点的费用值。我们算法的关键部分就是 h(n) 的设计,它会大大影响算法的效果和性能。
前面已经说过了,我们的任务目标是最大化 Pr(p|q,u,D),它等同于最小化负对数 -logPr(p|q,u,D)。给出一条可能的路径
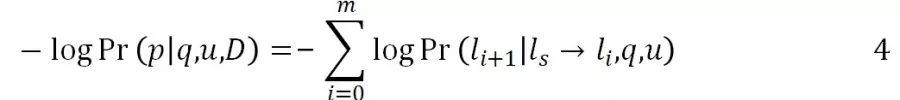
因此,对于一条路径

为了方便计算条件转移概率,在传统 A* 算法费用函数的计算中,一阶马尔可夫假设经常被使用,因此我们有
NASR模型结构

本文的网络主要分为两部分:g() 和 h(),分别对应于 A* 搜索算法中的两个 Cost:g 和 h。g() 学习的是从起点到候选位置的费用,我们称之为可观测费用,而 h() 学习的是从候选位置到终点的费用,我们称之为估计费用。在设计这两个网络的时候,需要满足一些要求:
1. 如何衡量已知路径的费用:怎样捕获用户的个性化偏好,时空特征以及路网限制呢? 用户的每一次的选择都会带来费用,这个费用跟用户的历史信息有关,跟时空信息也有关,并且还受到了路网邻接关系的影响。
2. 如何去衡量未来的费用:给定候选位置和终点,如何衡量这两个位置之间的费用呢? 类似于衡量路网上两个点的距离,在考虑用户偏好的前提下,怎样建模路网上两个位置之间潜在的费用是一个很重要的问题。
特征嵌入:
首先我们介绍多源输入信息的嵌入。通过词嵌入技术,我们将离散的用户信息嵌入到一个低维向量中,用 Vu 来表示。对于每一个位置,我们也使用相似的方法将这个位置嵌入到一个低维向量中,用 Vl 来表示。另外,我们又引入了时间信息,用 Vdi(b) 来表示天的向量,Vhi(b) 来表示小时的向量。最后这四者会被拼接起来成为循环神经网络的输入:

g网络的设计:
我们采用 GRU(门控循环单元)来建模轨迹:


在这里

上式中

上式中

上式中

最后我们采用交叉熵来进行优化:

h网络的设计:
对于 h 函数,我们使用图神经网络来建模。

上式中

在这里

我们将 A 个参数不同的注意力机制计算的结果拼接起来,


因此,h() 函数可以被以下式子近似,这个式子代表了未来奖励之和:

上式中,γ 是折扣因子,T 是到达终点时的时间步骤数,距离当前时间点越远,那么这个奖励就需要被打的折扣越多。进一步,通过时间差分法,我们可以将时间差分学习的标签写成如下形式。

预测误差可以被写成如下形式:
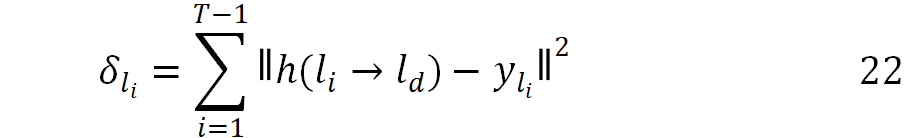
最终对于所有用户,所有轨迹的损失函数可以被定义成如下形式:

实验结果


表 2 是模型的性能,对比的都是经典或者最新的算法,可以看出本文的模型表现最佳。图 2 展示了注意力机制,图注意力神经网络以及时序差分学习对于性能的帮助。


图 3 展示了图注意力机制的有效性,我们可视化了路网上每个节点与起点和终点的相似度之和,可以发现,通过图注意力机制,我们的模型可以更多地关注那些可能经过的路网上的节点。而图 4 则展示了我们 h 网络的有效性,通过 h 网络,算法的搜索空间被大大减小了,避免了很多无谓的搜索。
总结
作者提出使用神经网络来学习 A* 搜索中的费用函数,并专门设计了两个网络。这两个网络建模了用户的偏好并充分利用了路网的结构信息,取得了非常好的效果。
按照本文的思路,未来可以尝试设计不同的神经网络来适应不同的路径规划任务,从而满足用户不同的需求。更多关于大数据与城市计算的论文以及相关代码数据请访问:https://www.bigscity.com/。





方面的Java封装,包含常用的一些处理方法,如滤波、信号变换等等。...)


__Python序列)








...)

