一、L1、L2 loss (分割中不常用,主要用于回归问题)
- L1 Loss
L1 Loss 主要用来计算 input x 和 target y 的逐元素间差值的平均绝对值.
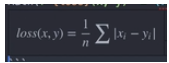
pytorch表示为:
- torch.nn.functional.l1_loss(input, target, size_average=True)
size_average主要是考虑到minibatch的情况下,需要求平均。

loss = nn.L1Loss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target) #是一个标量
output.backward()
# 求这个标量loss对每个input元素的梯度 可以用input.grad显示出来L2 损失(MSE loss)L2 LossL2 loss
L2 Loss 主要用来计算 input x 和 target y 的逐元素间差值平方的平均值.
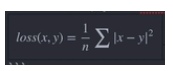
pytorch中表示为:
- torch.nn.functional.mse_loss(input, target, size_average=True)
具体应用不再介绍。
二、交叉熵损失
首先介绍一下交叉熵损失函数的由来,其中将介绍为什么交叉熵可以用于分类或分割,以及在one-hot多类别分类以及0-1编码二分类之间的区别;
1、从KL散度到交叉熵损失
如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x),我们可以使用 KL 散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异:
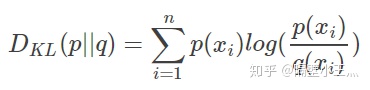
变形可以得到:
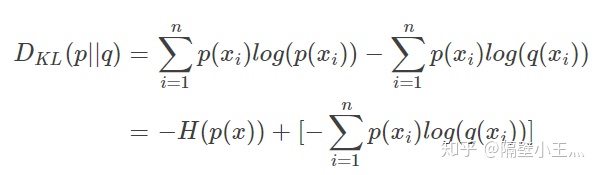
等式的前一部分恰巧就是p的熵,等式的后一部分,就是交叉熵:
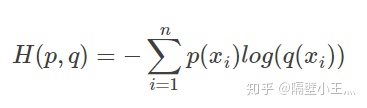
在一般的机器学习任务中,我们需要评估label和predicts之间的差距;上式中:P(x)代表label、q(x)代表predicts;由于label本身的熵是不变的,因此我们只需要关注后面的交叉熵就可以了。所以一般机器学习任务中直接使用交叉熵作为loss,用于评估模型。
2. 多分类任务中的one-hot编码下的交叉熵(当然one-hot也可以用于二分类)
首先介绍softmax操作,如图:
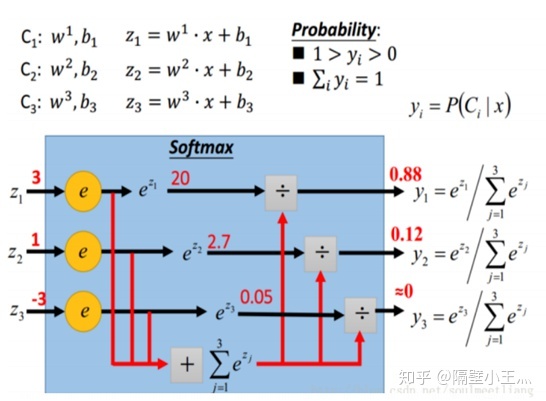
softmax的输出是一种归一化的分类概率,它将输出z首先经过指数级别进行差别放大,之后归一化到0到1之间。可以让大的数变得更大,小的数变得更小,最终所有的值归一化到0、1之间。
在数学上:

直观上看:
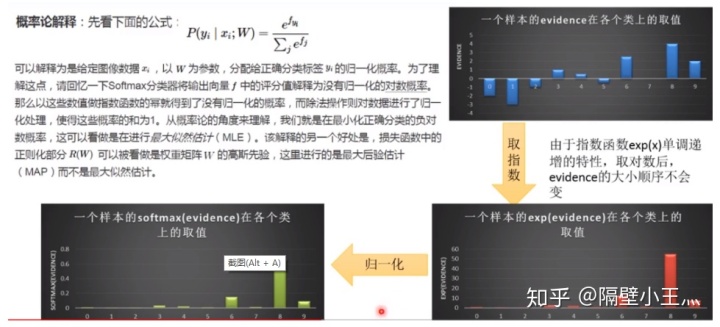
如何知道softmax的输出和真实label之间的差距呢?(计算交叉熵损失)
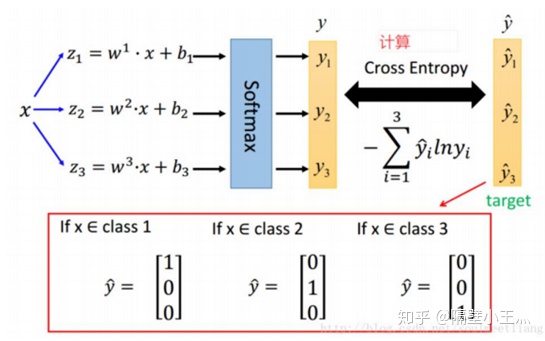
计算出来的y和y hat都是两个vector,和都是1,并且都相同的维度,可以理解为两个离散的概率分布。这样就可以衡量softmax输出的概率分布和label的one-hot分布之间的差距。使用交叉熵。
one-hot下的交叉熵表示为(上面z符号用x表示了哈):
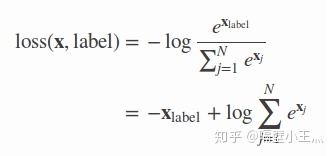
因为除了label位置对应的y hat为1,其余均是0;最终只剩一项
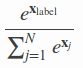
换个角度:对于这个loss,我们希望的是x label越来越大,其他x项越来越小;loss得到之后,更新都是原有的值减去lr*梯度;需要类别x label对应的梯度是负值,其他对应的梯度为正值。从loss可以很容易看出来哈!!!
pytorch中与Cross Entropy相关的loss Function(one-hot形式):
- CrossEntropyLoss: combines LogSoftMax and NLLLoss in one single class,也就是说我们的网络不需要在最后一层加任何输出层,该loss Function为我们打包好了;
- NLLLoss: 也就是negative log likelihood loss,如果需要得到log分布,则需要在网络的最后一层加上LogSoftmax
- NLLLoss2d: 二维的negative log likelihood loss,多用于分割问题(目前已经整合到NLLLoss)

3. 二分类0-1编码:output的编码不是one-hot,只是0代表1类,1代表一类;
真实的分布就是0和1;
预测的分布就是:如果是1的话就是f(x),0的话自然就是1-f(x);
我们希望这个loss损失达到最大值;

将上式进行归纳:

本质上就是交叉熵在伯努利分布上的表现形式,即:

二分类用的交叉熵,用的时候需要在该层前面加上 Sigmoid 函数。将输出值变到0到1之间;











)








