1. 题目

给你一个下标从 0 开始的二维整数数组 grid ，它的大小为 m x n ，表示一个商店中物品的分布图。数组中的整数含义为：

• 0 表示无法穿越的一堵墙。
• 1 表示可以自由通过的一个空格子。
• 所有其他正整数表示该格子内的一样物品的价格。你可以自由经过这些格子。

从一个格子走到上下左右相邻格子花费 1 步。

同时给你一个整数数组 pricing 和 start ，其中 pricing = [low, high] 且 start = [row, col] ，表示你开始位置为 (row, col) ，同时你只对物品价格在 闭区间 [low, high] 之内的物品感兴趣。同时给你一个整数 k 。

你想知道给定范围 内 且 排名最高 的 k 件物品的 位置 。排名按照优先级从高到低的以下规则制定：

• 距离：定义为从 start 到一件物品的最短路径需要的步数（较近 距离的排名更高）。
• 价格：较低 价格的物品有更高优先级，但只考虑在给定范围之内的价格。
• 行坐标：较小 行坐标的有更高优先级。
• 列坐标：较小 列坐标的有更高优先级。

请你返回给定价格内排名最高的 k 件物品的坐标，将它们按照排名排序后返回。
如果给定价格内少于 k 件物品，那么请将它们的坐标 全部 返回。

示例 1：

输入：grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], 
pricing = [2,5], start = [0,0], k = 3
输出：[[0,1],[1,1],[2,1]]
解释：起点为 (0,0) 。
价格范围为 [2,5] ，我们可以选择的物品坐标为 (0,1)，(1,1)，(2,1) 和 (2,2) 。
这些物品的排名为：
- (0,1) 距离为 1
- (1,1) 距离为 2
- (2,1) 距离为 3
- (2,2) 距离为 4
所以，给定价格范围内排名最高的 3 件物品的坐标为 (0,1)，(1,1) 和 (2,1) 。

示例 2：

输入：grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], 
pricing = [2,3], start = [2,3], k = 2
输出：[[2,1],[1,2]]
解释：起点为 (2,3) 。
价格范围为 [2,3] ，我们可以选择的物品坐标为 (0,1)，(1,1)，(1,2) 和 (2,1) 。
这些物品的排名为： 
- (2,1) 距离为 2 ，价格为 2
- (1,2) 距离为 2 ，价格为 3
- (1,1) 距离为 3
- (0,1) 距离为 4
所以，给定价格范围内排名最高的 2 件物品的坐标为 (2,1) 和 (1,2) 。

示例 3：

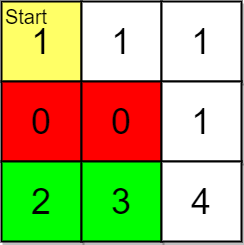
输入：grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3
输出：[[2,1],[2,0]]
解释：起点为 (0,0) 。
价格范围为 [2,3] ，我们可以选择的物品坐标为 (2,0) 和 (2,1) 。
这些物品的排名为：
- (2,1) 距离为 5
- (2,0) 距离为 6
所以，给定价格范围内排名最高的 2 件物品的坐标为 (2,1) 和 (2,0) 。
注意，k = 3 但给定价格范围内只有 2 件物品。提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 10^5
1 <= m * n <= 10^5
0 <= grid[i][j] <= 10^5
pricing.length == 2
2 <= low <= high <= 10^5
start.length == 2
0 <= row <= m - 1
0 <= col <= n - 1
grid[row][col] > 0
1 <= k <= m * n

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/k-highest-ranked-items-within-a-price-range
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

• BFS 遍历 地图，记录步数，价钱，横纵坐标
• 对答案进行排序输出

class Solution:from collections import dequedef highestRankedKItems(self, grid: List[List[int]], pricing: List[int], start: List[int], k: int) -> List[List[int]]:m, n = len(grid), len(grid[0])ans = []vis = [[False for _ in range(n)] for _ in range(m)]dir = [[1,0],[0,1],[-1,0],[0,-1]]q = deque([])q.append(start)vis[start[0]][start[1]] = Truestep = 0while len(q):size = len(q)for _ in range(size):x, y = q[0]q.popleft()if pricing[0] <= grid[x][y] <= pricing[1]:ans.append((step, grid[x][y], x, y))if grid[x][y] > 0:for d in range(4):nx = x+dir[d][0]ny = y+dir[d][1]if nx>=0 and nx<m and ny>=0 and ny<n and not vis[nx][ny]:q.append([nx, ny])vis[nx][ny] = Truestep += 1ans.sort(key=lambda x : [x[0],x[1],x[2],x[3]])return [[x[2],x[3]] for x in ans[:k]]

1056 ms 53.5 MB Python3

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！