一、思考：连续分配方式的缺点？

考虑支持多道程序的两种连续分配方式：

1. 固定分区分配：缺乏灵活性，会产生大量的内部碎片，内存的利用率很低。
2. 动态分区分配：会产生很多外部碎片，虽然可以用“紧凑”技术来处理，但是“紧凑”的时间代价很高。
   如果允许将一个进程分散地装入到许多不相邻的分区中，便可充分地利用内存，而无需再进行“紧凑”。基于这一思想，产生了“非连续分配方式”，或者称为“离散分配方式”。
   
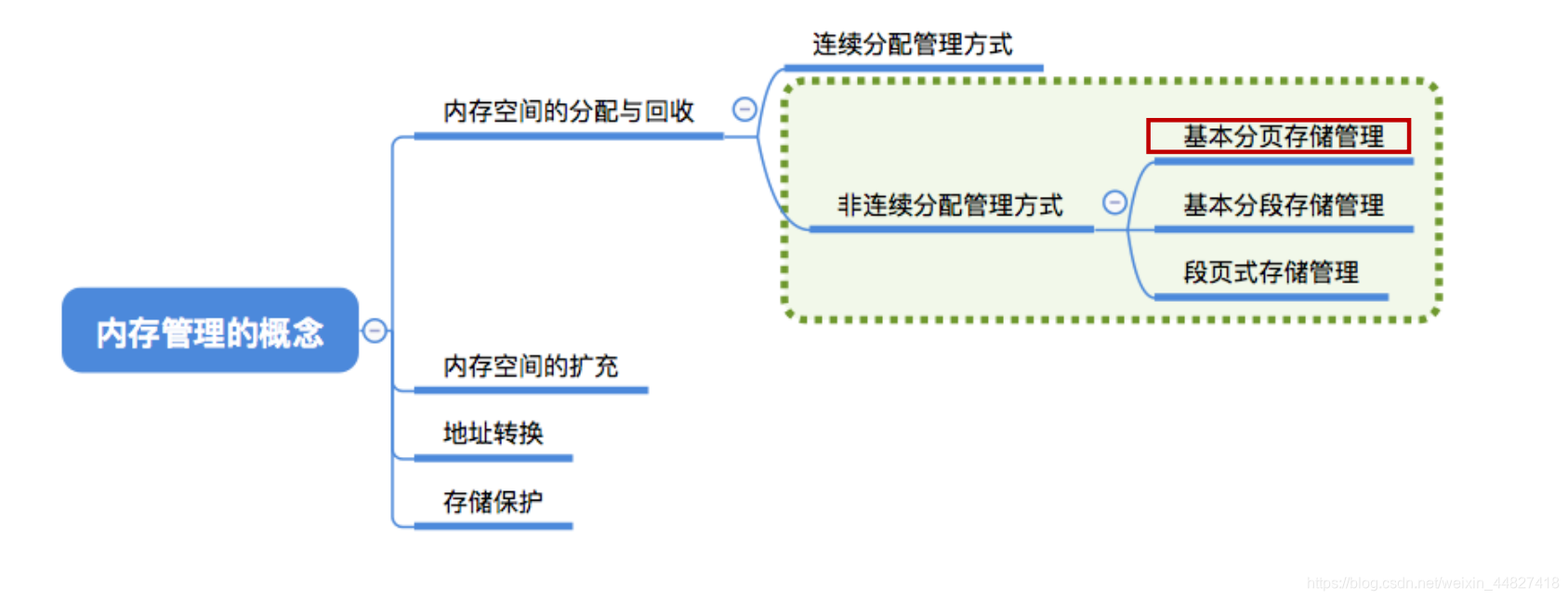
   连续分配：为用户进程分配的必须是一个连续的内存空间。
   非连续分配：为用户进程分配的可以是一些分散的内存空间。

二、把“固定分区分配”改造为“非连续分配版本”

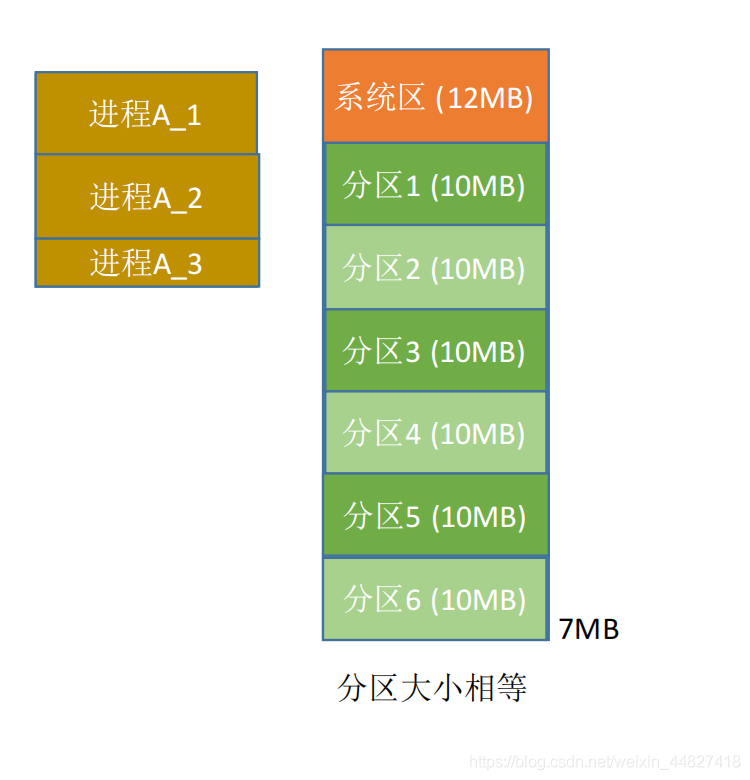
假设进程A大小为23MB，但是每个分区大小只有10MB，如果进程只能占用一个分区，那显然放不下。
解决思路：如果允许进程占用多个分区，那么可以把进程拆分成10MB+10MB+3MB三个部分，再把这三个部分分别放到三个分区中（这些分区不要求连续）。但是，进程A的最后一个部分是3MB，放入分区后会产生7MB的内部碎片。

如果每个分区大小为2MB，那么进程A可以拆分成11*2MB+1MB共12个部分，只有最后一部分1MB占不满分区，会产生1MB的内部碎片。
显然，如果把分区大小设置的更小一些，内部碎片会更小，内存利用率会更高。
基本分页存储管理的思想——把内存分为一个个相等的小分区，再按照分区大小把进程拆分成一个个小部分

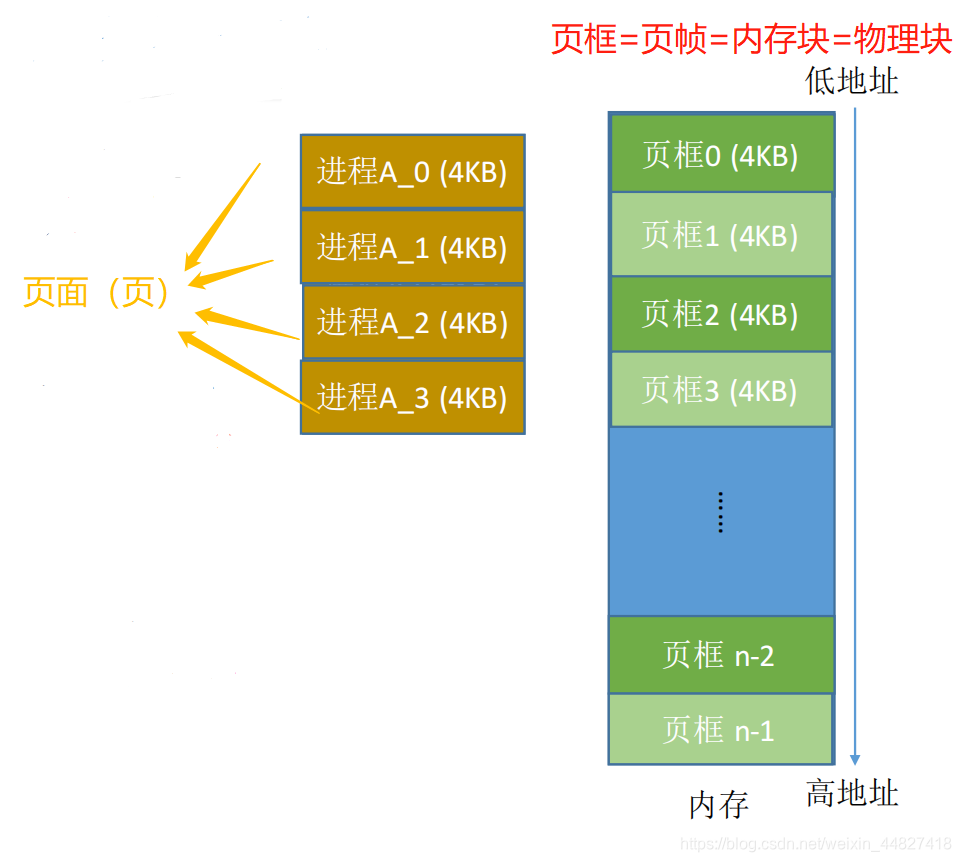
三、分页存储管理的基本概念

将内存空间分为一个个大小相等的分区（比如：每个分区4KB），每个分区就是一个“页框”，或称“页帧”、“内存块”、“物理块”。每个页框有一个编号，即“页框号”（或者“内存块号”、“页帧号”、“物理块号”）页框号从0开始。

将用户进程的地址空间也分为与页框大小相等的一个个区域，称为“页”或“页面”。每个页面也有一个编号，即“页号”，页号也是从0开始。
（注：进程的最后一个页面可能没有一个页框那么大。因此，页框不能太大，否则可能产生过大的内部碎片）

操作系统以页框为单位为各个进程分配内存空间。进程的每个页面分别放入一个页框中。也就是说，进程的页面与内存的页框有一一对应的关系。各个页面不必连续存放，也不必按先后顺序来，可以放到不相邻的各个页框中。

四、思考：如何实现地址的转换？

将进程地址空间分页之后，操作系统该如何实现逻辑地址到物理地址的转换？

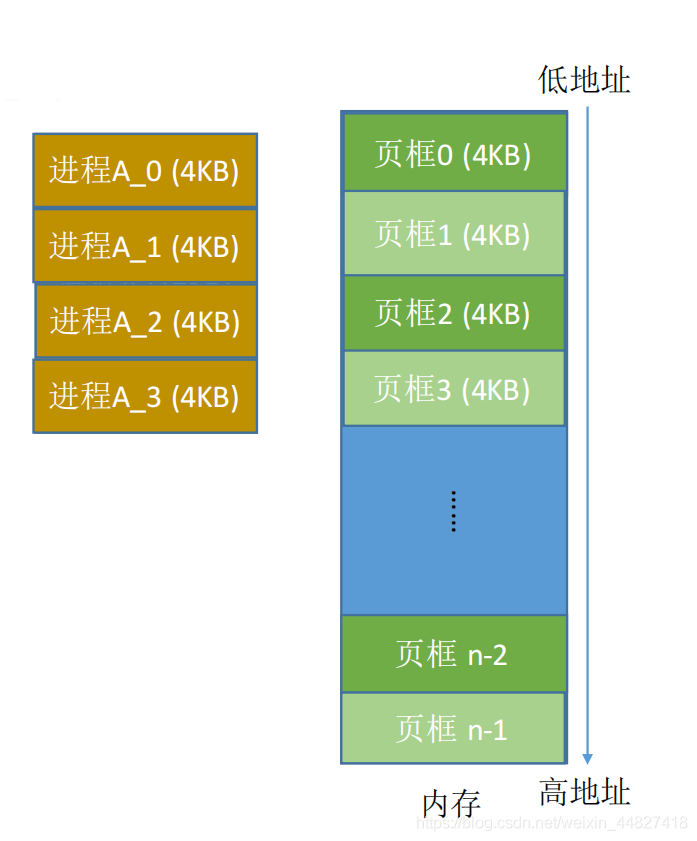
先回顾一下，进程在内存中连续存放时，操作系统是如何实现逻辑地址到物理地址的转换的？（采取动态重定位的方法）

五、如果采用分页技术，应该如何实现地址转换？

CPU执行指令1，需要访问逻辑地址为80的内存单元，如何转化为物理地址？

逻辑地址为80的内存单元：
应该在1号页，该页在内存中的起始位置为450，逻辑地址为80的内存单元相对于该页的起始地址而言，“偏移量”应该是30。
所以，实际物理地址=450+30=480

1. 要算出逻辑地址对应的页号
2. 要知道该页号对应页面在内存中的起始地址
3. 要算出逻辑地址在页面内的“偏移量”
4. 物理地址=页面始址+页内偏移量

如何计算：
页号=逻辑地址/页面长度（取除法的整数部分）
页内偏移量=逻辑地址%页面长度（取除法的余数部分）
页面在内存中的起始位置：操作系统需要用某种数据结构记录进程各个页面的起始位置。

页号=80/50=1
页内偏移量=80%50=30
1号页在内存中存放的起始位置450
注意：为了方便计算页号、页内偏移量，页面大小一般设为2的整数幂

结论：如果每个页面大小为2^K B，用二进制数表示逻辑地址，则末尾K位即为页内偏移量，其余部分就是页号
因此，如果让每个页面的大小为2的整数幂，计算机就可以很方便地得出一个逻辑地址对应的页号和页内偏移量。

六、逻辑地址结构

分页存储管理的逻辑地址结构如下所示：

地址结构包含两个部分：前一部分为页号，后一部分为页内偏移量W。在上图所示的例子中，地址长度为32位，其中0-11位为“页内偏移量”，或称“页内地址”；12-31位为“页号”。
如果有K位表示“页内偏移量”，则说明该系统中一个页面的大小是2^K个内存单元
如果有M位表示“页号”，则说明在该系统中，一个进程最多允许有2^M个页面

分页存储管理中，如何实现地址转换？

1. 要算出逻辑地址对应的页号
2. 要知道该页是对应页面在内存中的起始地址
3. 要算出逻辑地址在页面内的“偏移量”
4. 物理地址=页面始址+页内偏移量
   注：如果题目中是用十进制数表示逻辑地址，则页号=逻辑地址/页面长度（取除法的整数部分）页内偏移量=逻辑地址%页面长度（取除法的余数部分）

七、页表

为了能知道进程的每个页面在内存中存放的位置，操作系统要为每个进程建立一张页表。

为什么每个页表项的长度是相同的，页号是“隐含”的？
Eg：假设某系统物理内存大小为4GB，页面大小为4KB，则每个页表项至少应该为多少字节？
4GB=2^32B，
4KB=2^12B
因此4GB的内存总共会被分为2^32 / 2^12= 2^{20个内存块**，因此内存块号的范围应该是0~2}20-1因此至少要20个二进制位才能表示这么多的内存块号，因此至少要3个字节才够（每个字节8个二进制位，3个字节共24个二进制位）

各页表项会按顺序连续地存放在内存中。如果该页表在内存中存放的起始地址为x，则M号页对应的页表项一定是存放在内存地址为 X+3*M。因此，页表中的“页号”可以是“隐含”的。
只需要知道页表存放的起始地址和页表项长度**，即可找到各个页号对应的页表项存放的位置。在本例中，一个页表项占3B，如果进程由n个页面，则该进程的页表总共会占3*n个字节。

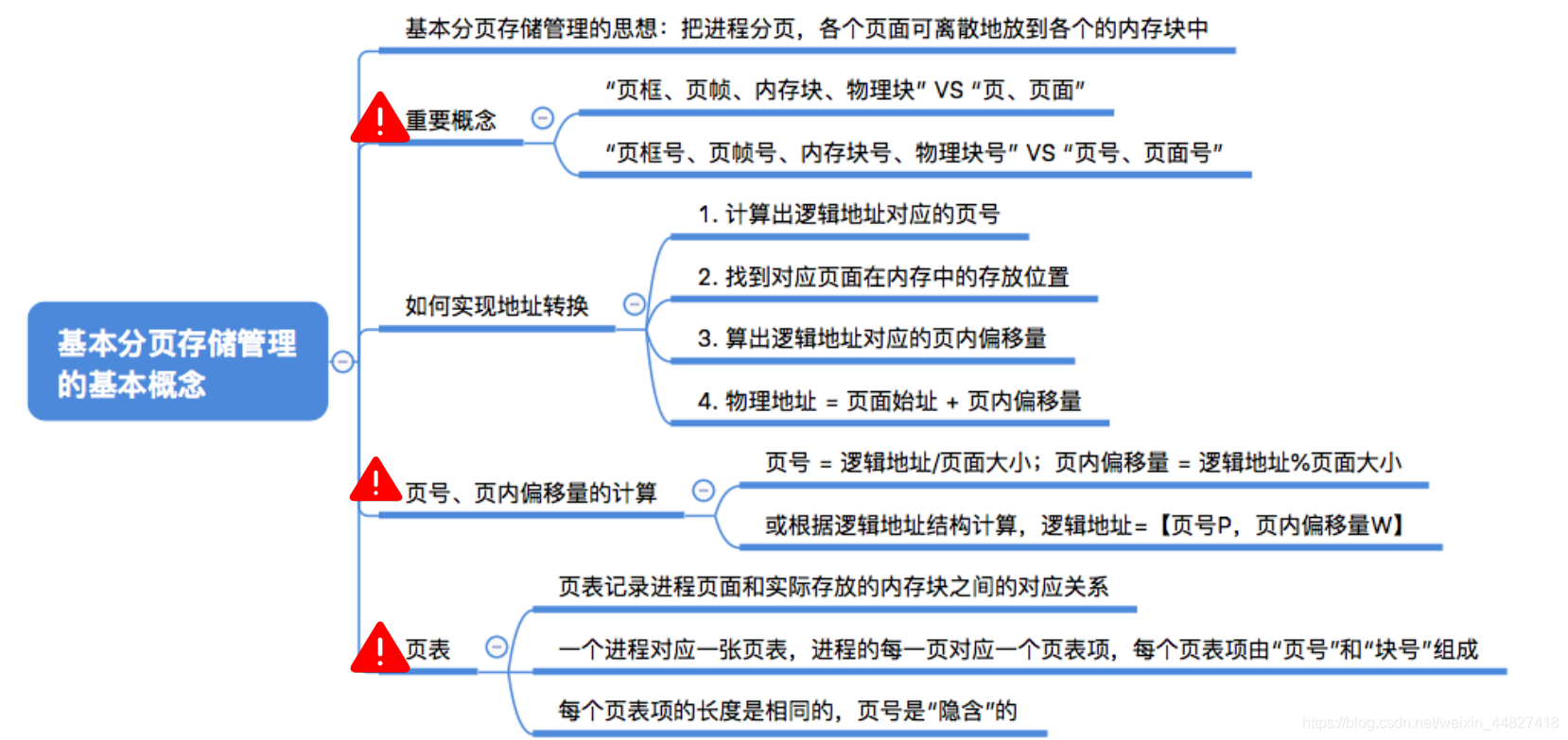
八、总结