1 概述

有背景音乐的短视频拼接时，如果两个视频的拼接点刚好在背景音乐的某个节拍点上，那么合成的视频看起来，听起来，都会非常舒服，这是短视频合成的一个加分项，这种视频也就是我们经常说的卡点视频。要做卡点视频的前提是找到背景音乐中可以卡的点，beats是其中一种可以卡的点，本文就是用大白话来讲讲论文Beat Tracking by Dynamic Programming是怎么找beats的。常用的音频信号处理库librosa中的librosa.beat.beat_track用的就是这种方法。这个任务的名字叫做beat tracking，下文中都将这样称呼。

2 总体框架

论文中介绍的beat tracking可以分为三个步骤：

（1）计算Onset Strength Envelope（Onset的能量包络）

（2）计算全局的Tempo

（3）基于动态规划计算beats

我第一次看到这三步，也是一头雾水，如果是专门做信号处理的人，可能已经知道怎么回事了，但这篇文章的的目标受众是像我一样，学过或者了解过信号处理却已经忘的差不多的小伙伴。所以，下面会针对这三个步骤详细解析。

如果只想知道怎么使用的话，librosa已经为我们包装好了一切，三行代码就搞定了。

import librosay, sr = librosa.load(“your/music/file/path”)
tempo, beats = librosa.beat.beat_track(y=y, sr=sr)

3. 计算Onset Strength Envelope

onset指的就是某个音符发出声音的起点，比如按下钢琴键的那个时刻，又比如拨动琴弦的那个时刻，下图示意了onset的位置。在这个环节中，就是要把一段音频中所有的onset的能量包络找出来。给到的音频可能是有鼓的音轨，钢琴的音轨，小提琴的音轨，人声的音轨等混合在一起的。不管哪个音轨的，都会被我们找出来。

图1：onset示意图

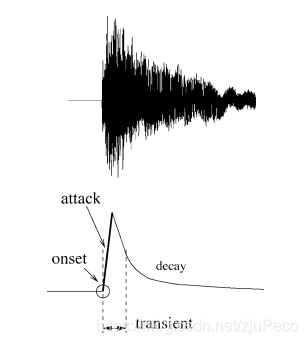
找onset能量包络的方法不是这篇论文提出来的，用的是一个已有的常用的方法，叫做crude perceptual model。其步骤如下所示：

（1）用8kHz的采样率读取音频文件。

（2）用32ms的window_size和4ms的step_size，进行短时傅立叶变换(STFT)，得到图2中最上方的图。

（3）将频谱图映射到梅尔频谱上，纵轴分为40个bands，得到图2中中间的图。

（4）沿时间轴对每个band做一阶差分，并把所有的负值置0，再把每个时间点的所有band差分后的正值累加。

（5）对（4）中得到的结果进行高通滤波，过滤掉0.4kHz以下的信息，使其局部零均值，再用window_size为20ms高斯窗做平滑处理，得到图2中最下方的图，也就是onset strength envelope，记作$O(t)$。

图2：频谱，梅尔频谱和onset strength envelope的对比图

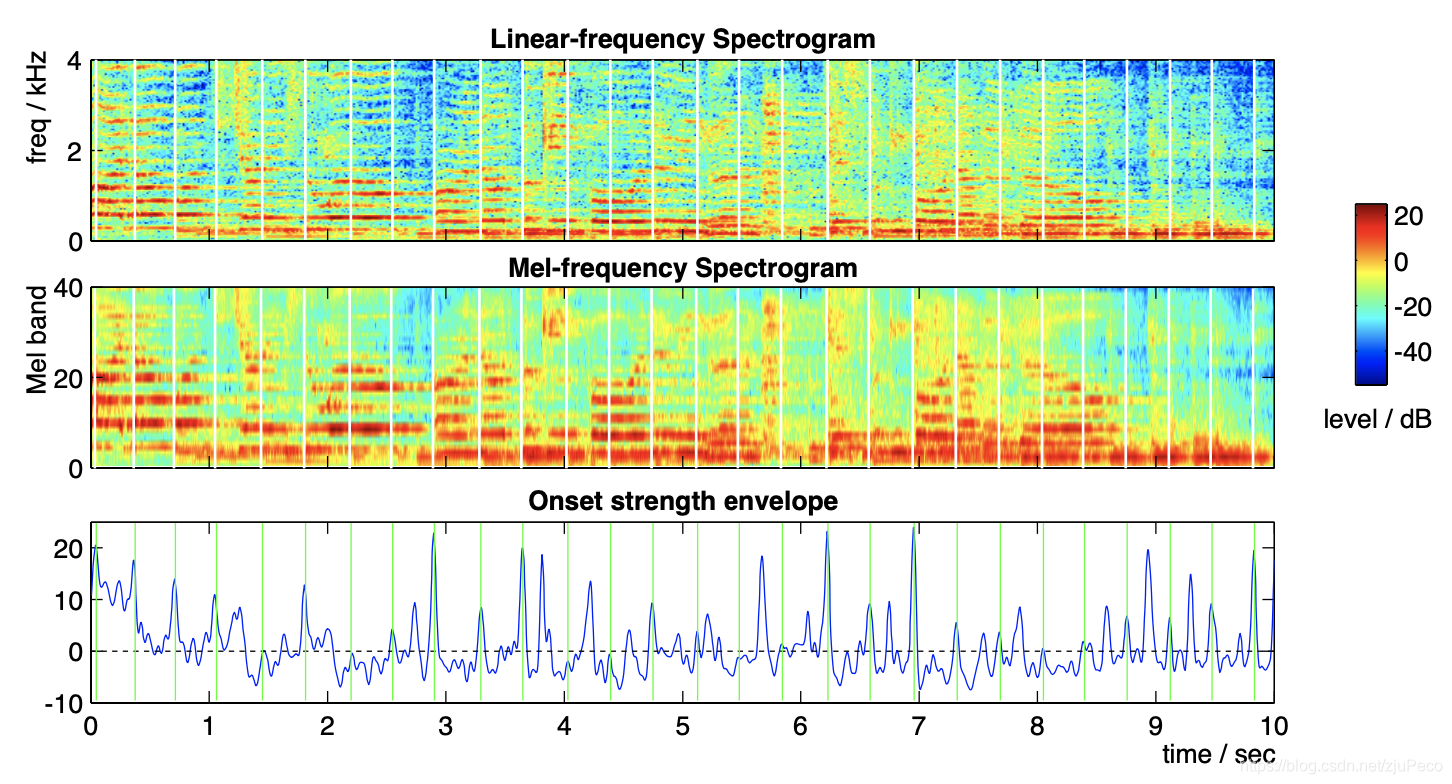
$O(t)$中的各个局部峰值就是能量突增的地方，为什么会能量变化剧烈？当然是因为有新的音符发声了。注意，这里的波峰我认为不是onsets的精确时间，而是onsets产生的波峰的时间。不过不同的文章中好像都是把这个onsets的候选了。不过我们不关心onsets具体到底在哪里，只要有$O(t)$就够了，所以不纠结定义问题了。

还有一个就是，我比较奇怪论文的作者为什么要用（5）这样的归一化方式，这样得到的$O(t)$就会有很多负值，但是这些负值我们是不要的。Tempo and Beat Tracking中的归一化方式我觉得更合理一些，直接减去local average，就可以了。下图3中的最上方红线就是local average，减去后得到的结果为图3中间的那个图，图3下方的图标出了局部峰值和onsets。

图3：onset strength envelope归一化处理

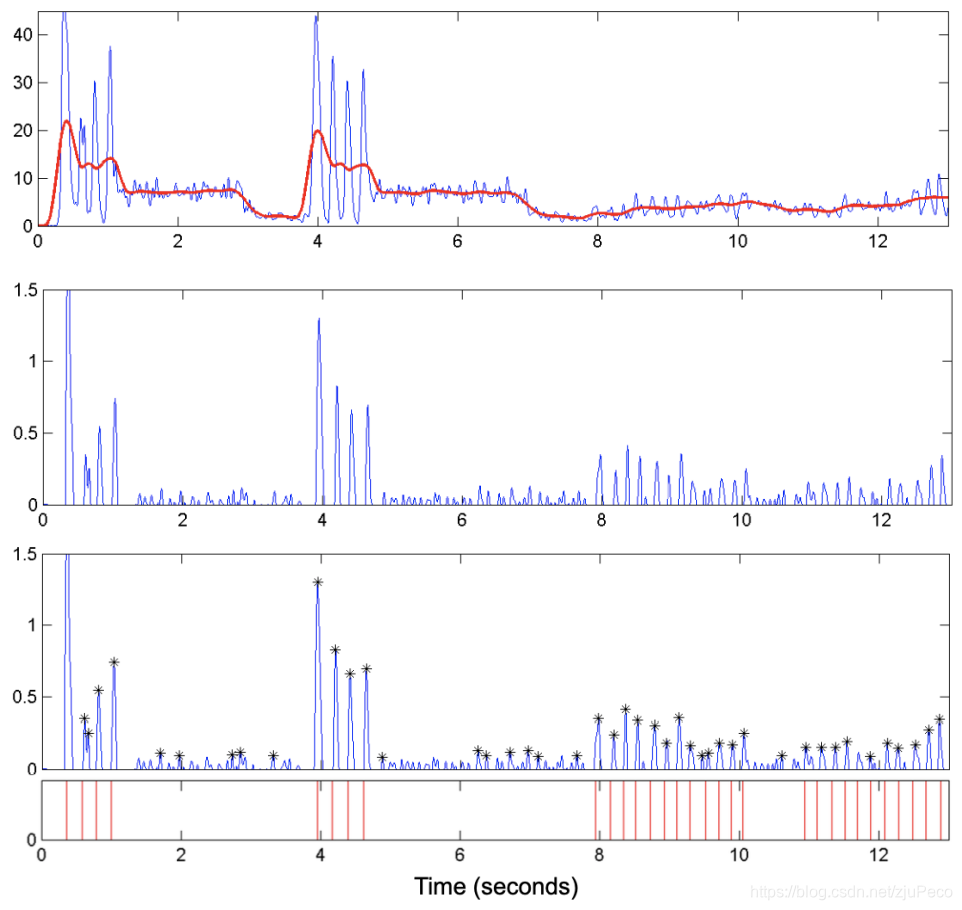
4 计算全局的Tempo

Tempo指的是音乐的节拍，通常用bpm(beats per minute)来度量，比如120bpm就表示一分钟有120个beats，拍子的周期为0.5s。本文中用拍子的周期来表示Tempo。一首音乐的Tempo有可能是随时间变化的，但这种情况很少，我们这里只讨论整个音频的tempo都保持一致的情况。变化的Tempo检测可以参见predominant local pulse，大致思想就是分段处理，这里不讨论。

节拍就是一个调子在不断循环，我们要找出这个循环的周期。自相关函数用来找周期是在适合不过的了，我们会计算不同延迟时间下$O(t)$的自相关函数值，值最高的对应的延迟时间就是一个beat的长度。

但是这里有一个问题，如图4的raw autocorrelation所示，周期函数的在他基周期的倍数上的自相关函数值都是很大的。为了解决这个问题，论文引入了一个权重系数，使得周期结果偏向于某个经验值。这个计算自相关系数的计算公式为

$$TPS(\tau )=W(\tau )\sum _{t}O(t)O(t-\tau )$$

其中，$\tau$是延迟的时间，TPS为Tempo Period Strength的缩写，是论文作为给这个自相关计算方法取的名字，使得$TPS(\tau )$最大的那个$\tau$，就是我们要找的周期。

$W(\tau )$是一个高斯权重系数，表示为

W(τ)=exp{−12(log2τ/τ0στ)2}W(\tau) = exp\{-\frac{1}{2}(\frac{log_2 \tau / \tau_0}{\sigma_\tau})^2\} W(τ)=exp{−21​(στ​log2​τ/τ0​​)2}

其中，${\tau }_0$就是默认偏向的周期大小，${\sigma }_{\tau }$是表示偏重程度的一个系数。${\tau }_0$和${\sigma }_{\tau }$都是经验值，论文从MIREX-06 Beat Tracking训练集中统计得来的。统计的方法是填入不同的${\tau }_0$和${\sigma }_{\tau }$，使得$TPS(\tau )$的得出的最大值和数据中标注的Tempo一致性最高的那组${\tau }_0$和${\sigma }_{\tau }$就是了。

最终得出的${\tau }_0$为0.5s，也就是120bpm，${\sigma }_{\tau }$为1.4。在该组参数下的$TPS(\tau )$如图4中最下方的图所示。图中的Primary Tempo Period就是最终的周期。

图4：onset strength envelope，原始自相关函数和TPS的对比图

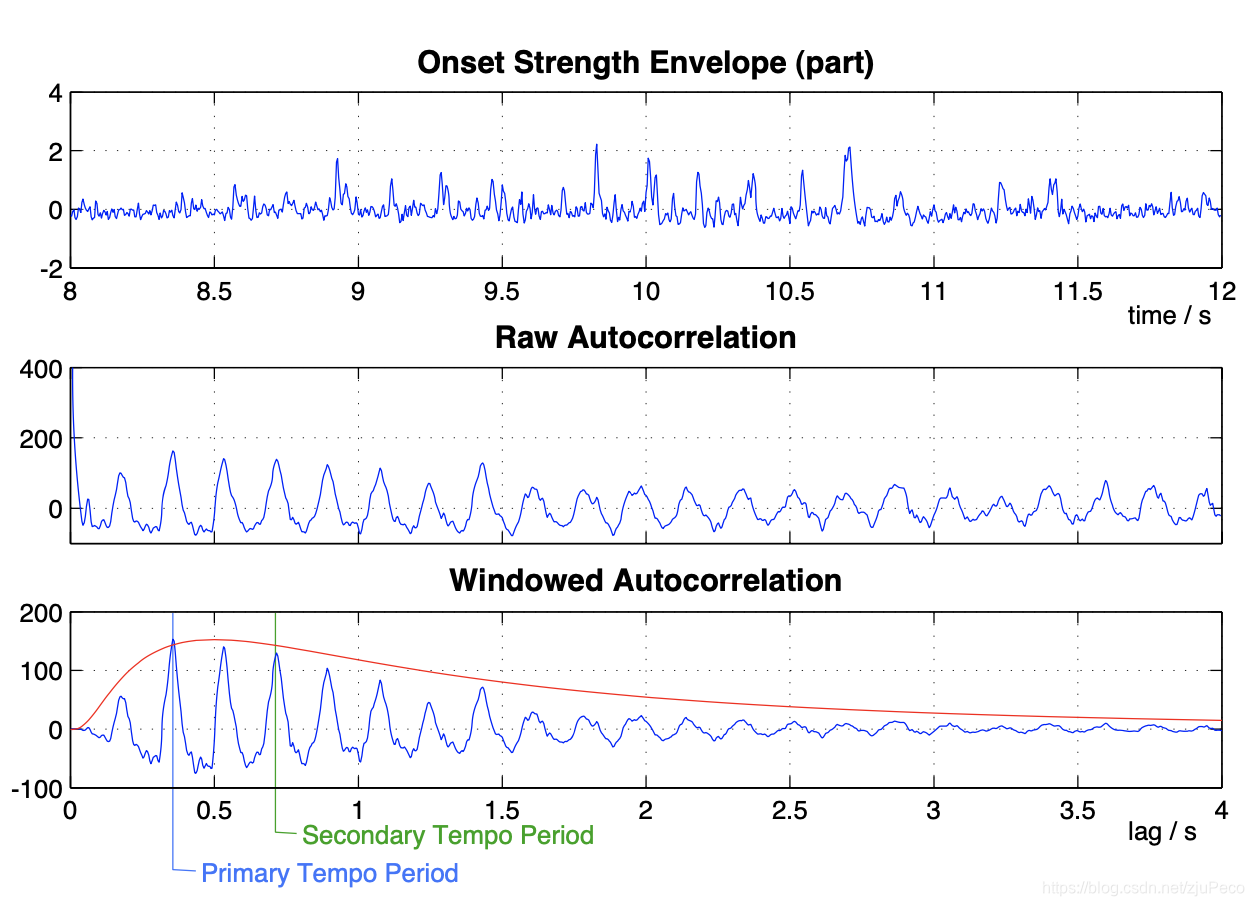
librosa.beat.beat_track中有一个输入参数为start_bpm，指的就是${\tau }_0$，可以人为传入修改，默认为120。

在实际的使用中，会对$TPS(\tau )$做一些优化，变成

$$TPS2(\tau )=TPS(\tau )+0.5TPS(2\tau )+0.25TPS(2\tau -1)+0.25TPS(2\tau +1)$$

或是

$$TPS3(\tau )=TPS(\tau )+0.33TPS(3\tau )+0.33TPS(3\tau -1)+0.33TPS(3\tau +1)$$

不管用哪种方法，$TPS(\tau )$的峰值对应的$\tau$就是我们要找的周期。

5 基于动态规划计算beats

论文以4ms一个步长（250Hz）将时间分段，利用了第3节和第4节的结果，设计了如下的目标函数：
C({ti})=∑i=1NO(t)+α∑i=2NF(ti−ti−1,τp)C(\{t_i\}) = \sum_{i=1}^N O(t) + \alpha \sum_{i=2}^N F(t_i - t_{i-1}, \tau_p) C({ti​})=i=1∑N​O(t)+αi=2∑N​F(ti​−ti−1​,τp​)

其中，{ti}\{t_i\}{ti​}为找到的$N$个beats；$O(t)$就是第3节中的Onset Strenghth Envelope；$\alpha$为平衡两个目标项的系数；${\tau }_p$就是第4节中得到的周期；$F(△t,{\tau }_p)$是用来衡量每两个相邻的beats的间距和${\tau }_p$的差距，这个可以自己定义，论文中表示为

$$F(△t,{\tau }_p)=-(log\frac{△t}{{\tau }_p}{)}^2$$

可见当$△t$和${\tau }_p$越接近，$F(△t,{\tau }_p)$越大，最大为0，否则越小。除此之外，该式是log对称的，比如$F(k{\tau }_p,{\tau }_p)=F({\tau }_p/k,{\tau }_p)$。

我们的目标是使得C({ti})C(\{t_i\})C({ti​})越大越好，分析一下，当$\alpha =0$时，把所有的时间点全部选上，C({ti})C(\{t_i\})C({ti​})就最大了；当$\alpha =+\infty$时，选择时间间隔为${\tau }_p$的一组点就可以使得C({ti})C(\{t_i\})C({ti​})最大了。不难看出，有了$\alpha$的平衡，最终得到的点列就是间隔在${\tau }_p$左右微调，且使得点落$O(t)$局部峰值附近的一组点。

论文用动态规划的方法，以线性的时间复杂度，解决了这个问题。首先定义了$C^{\ast }(t)$，表示只考虑时间点不大于时刻$t$时，以时刻$t$为一个beat的C({ti})C(\{t_i\})C({ti​})的最大值，这也就是动态规划中的状态转移函数，其表达式为：

C∗(t)=O(t)+max⁡τ=0...t−4ms{αF(t−τ,τp)+C∗(τ)}C^*(t) = O(t) + \max_{\tau=0...t-4ms} \{\alpha F(t-\tau, \tau_p) + C^*(\tau)\} C∗(t)=O(t)+τ=0...t−4msmax​{αF(t−τ,τp​)+C∗(τ)}

这个和标准的动态规划还是有点区别，要细细品味一下，这个地方我思考了挺久，这种做法可以避免在计算状态转移时，之前的最优beats序列发生变化。这个$C^{\ast }(t)$还有一个好处，就是可以用来找结尾，当$C^{\ast }(t)$的增量骤减时，就是音乐转弱，也就是结尾的地方了。

同时，也会记录使得$C^{\ast }(t)$最大的那个序列在$t$之前的那个beat为

P∗(t)=argmax⁡τ=0...t−4ms{αF(t−τ,τp)+C∗(τ)}P^*(t) = arg\max_{\tau=0...t-4ms} \{\alpha F(t-\tau, \tau_p) + C^*(\tau)\} P∗(t)=argτ=0...t−4msmax​{αF(t−τ,τp​)+C∗(τ)}

也就是说取的$\tau$是多少。通过$P^{\ast }(t)$可以回溯选择的beats路径，得到最终的beats序列。

在实际搜索$\tau$的时候，不会从0到t-4ms去做的，这样会计算很多不必要的情况。有F的惩罚在，我们只要搜索$\tau =t-2{\tau }_p...t-{\tau }_p/2$。

我们把从0到总时长，所有的时刻$t$对应的$C^{\ast }(t)$都算出来之后，取其中最大的那个$C^{\ast }(t_N)$，$t_N$就是最后一个beat点，然后$t_{N-1}=P^{\ast }(t_N)$，然后由此一直回溯出整条序列{ti}\{t_i\}{ti​}。有一点可以确定的是，$t_N$必然在$[总时长-{\tau }_p,总时长]$的范围内，不然就还可以再加入一个beat。

说到这里正文已经说完了。这里再简单说一下，为什么不能按标准的动态规划的做法，不然下次自己来看可能又要想半天。按标准的做法，会定义$C^{\ast }(t_j)$为时间点不大于时刻$t_j$时，C({ti})C(\{t_i\})C({ti​})的最大值。状态转移函数为

C∗(tj)=max⁡{O(tj)+max⁡τ=0...tj−1{αF(tj−P∗(τ),τp)+C∗(τ)},C∗(tj−1)}C^*(t_j) = \max \{ O(t_j) + \max_{\tau=0...t_{j-1}} \{\alpha F(t_j-P^*(\tau), \tau_p) + C^*(\tau)\}, C^*(t_{j-1}) \} C∗(tj​)=max{O(tj​)+τ=0...tj−1​max​{αF(tj​−P∗(τ),τp​)+C∗(τ)},C∗(tj−1​)}

解释一下就是，有两种选择，前一种是把$t_j$作为一个beat，另一种是不把$t_j$作为一个beat。问题就处在这个$P^{\ast }(\tau )$，当我们把$t_j$作为一个beat，使得$C^{\ast }(t_j)$尽可能大的前一个beat不一定是$P^{\ast }(\tau )$。换而言之，把$t_j$作为一个beat后，前面的最优beats可能会发生变化。如果按标准的做法来，会漏掉许多时间点作为beat的情况。细品，细品。

6 参考文献

[1] Beat Tracking by Dynamic Programming
[2] Tempo and Beat Tracking