文章目录
- 1 概述
- 2 信号预处理
- 3 分类神经网络
- 4 动态贝叶斯网络(HMM)
- 4.1 原始的bar pointer model
- 4.2 原始的bar pointer model的缺点
- 4.3 改进后的模型
- 5 预测
- 参考资料
1 概述
最近在做音乐卡点相关的项目,需要对音乐的基本特征进行理解,比如beats和downbeats就是最基本的特征。madmom是我找到的一个对beats和downbeats的检测都有实现的第三方库,于是就认真学习了一下,把其中用到的方法和自己的理解记录下来。
madmom中的beats和downbeats检测就是复现了Joint Beat and Downbeat Tracking with Recurrent Neural Networks这篇论文,其核心思想就是HMM,如果对HMM没有扎实的理解的话,建议先看我写的另一篇搞懂HMM。本文不会对HMM的基本概念做详细的说明。
在说论文之前,我先来说明一些音乐上的专用术语,对齐一些概念,便于后文的叙述。有些术语在本文中可能不会再次出现,但有助于理解音乐,就一并写上了。
| 名词 | 名词解释 |
|---|---|
| 拍子(beat) | 在音乐中,时间被分成均等的基本单位,每个单位叫做一个“拍子”或称一拍。 |
| 强拍(downbeat) | 音乐中的强拍。是beats的子集。一般是每个小节的起始beat |
| 小节(measure/bar) | 音乐是由强拍和弱拍交替进行的,是按照一定的规律构成最小的节拍组织一小节,然后以此为基础循环往复。一个小节一般有2拍,3拍,4拍或者6拍等等 |
| 节拍(meter) | beats per measure,一首歌的节拍,一般表示为1/4拍或者2/4拍或者3/8拍等等。比如3/4拍表示4分音符为1拍,每小节有3拍,节拍强度为强、弱、弱。 |
| 全局节奏(tempo) | 一般用bpm(beats per minute)来做单位,表示每分钟有多少个beats,用来衡量音乐的速度,一首音乐可以由不同的tempo演奏。 |
| 局部节奏(tempi) | 每两个相邻的beats之间可以是有不同的1/16音符,或是1/8音符,或是1/4等组成的,这个就是局部节奏 |
| onset | 一个音符被乐器或者人发出声音的那个时刻点。 |
| 峰值(peak) | onset包络图的峰值,具体可见peak_pick。 |
再说回这篇论文。这篇论文概括地说就是把信号切成多个frames,每个frame会在RNN网络之后对应一个概率输出,表示该frame是beat还是downbeat还是都不是。HMM会在发射概率的计算中借助于这个RNN结果,把frame在measure当中的相对位置和tempi作为隐变量,得到最佳的隐变量路径,并把该路径解码为beats和downbeats。
下面会分步骤说明一下每个步骤,着重是HMM和预测部分。这两部分理解起来有点绕。
2 信号预处理
这部分其实就是一个类似于MFCC提取语音信号特征的过程,作为RNN的输入,这里简单说下。先是用汉宁窗对信号做了有交叠的分割,分成了100fps(frame per second),并基于此做了短时傅里叶变换(STFT)。丢弃了相位特征,只保留幅值特征,因为人耳是听不出相位的。为了保证时域和频域的精度,做STFT时,分别用了1024,2048和4096三种窗口大小。把频段限制在了[30, 17000]Hz的的范围,并给每个八度分了3,6和12个频段,分别对应于1024,2048和4096三种窗口大小。同时也对频谱进行了一阶差分,也作为特征concat进去。最终,输入网络的特征维度为314。
3 分类神经网络
这部分用了由LSTM搭建而成的网络,目的是给每个frame进行分类,输出两个概率值,(是beat的概率,是downbeat的概率),取较大的作为该frame的分类。为了避免混淆,downbeat不属于beat。
同时,也设置了θ=0.05\theta=0.05θ=0.05的阈值,只有大于该阈值,才会被判为是beat或者downbeat。这是为了减小音乐头尾有空白的干扰。
既然每个frame是beat还是downbeat的概率都知道了,那我直接取每个frame最大概率的类别,两个概率都比较小的就认为既不是beat也不是downbeat,这事不就成了?
理想很美好,现实并非如此,不要被论文中的图片给误导了,来看下模型的实际输出是长啥样的。
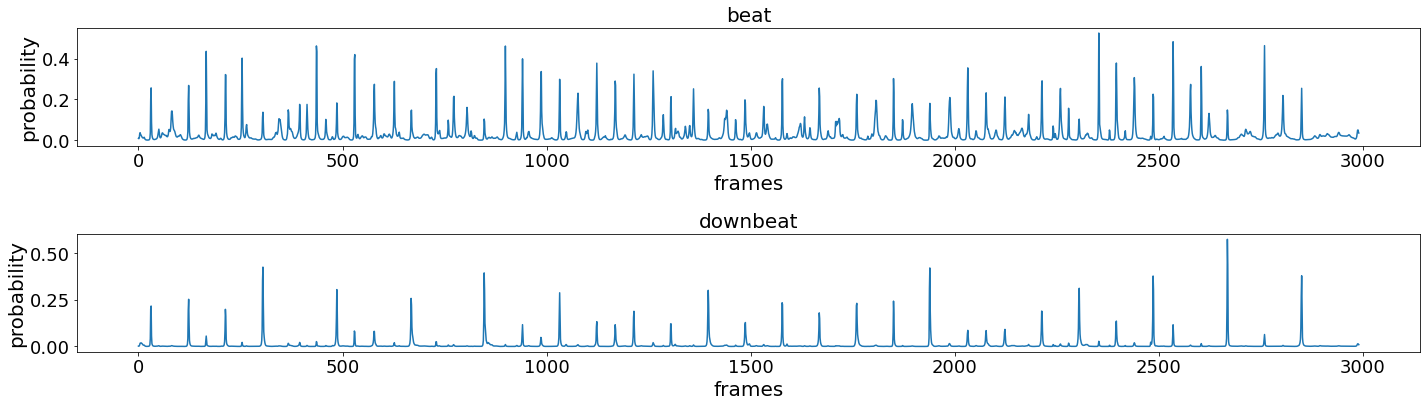
模型的输出如上图3-1所示,这个是一条30s左右的实际样例。上半个图是每个frame为beat的概率,下半个图是每个frame为downbeat的概率。只看downbeat这部分的话,不难看出概率比较高的frame之间的间距有长有短,而在一个小节(bar)当中,强拍(downbeat)应该只会出现一次,次强拍的出现会对其产生干扰。RNN不知道强拍的出现是有周期性的,所以需要HMM来判断究竟哪些位置是强拍,哪些位置是弱拍,哪些位置什么都不是。
从另一个角度来思考,RNN这里并不知道音乐的meter是几几拍,没有这个信息,要RNN直接判断强拍和弱拍的难度是很大的。下一节的HMM的作用就是根据RNN的结果,去选一组最优的beats和downbeats。
4 动态贝叶斯网络(HMM)
这是重点部分,我们来详细讲一下。Joint Beat and Downbeat Tracking with Recurrent Neural Networks对这部分的说明很不清晰,我们直接看它沿用的An Efficient State-Space Model for Joint Tempo and Meter Tracking中的说明即可。
4.1 原始的bar pointer model
早在2006年的时候,Bayesian Modelling of Temporal Structure in Musical Audio就提出过用HMM解决beat tracking问题的方法。现在的方法,就是在它的基础上优化的,我们先来看看最早版本的HMM是怎么设计的。
我们令第kkk个frame的隐变量为xk=[Φk,Φ˙k]\bold{x}_k=[\Phi_k, \dot{\Phi}_k]xk=[Φk,Φ˙k]。Φk∈{1,2,...,M}\Phi_k \in \{1,2,...,M\}Φk∈{1,2,...,M}表示第kkk个frame在某个小节(bar)中的相对位置,1表示起始位置,MMM表示结束位置,这个bar被分成了M个相对位置,一般是均分的。Φ˙k∈{Φ˙min,Φ˙min+1,...,Φ˙max}\dot{\Phi}_k \in \{\dot{\Phi}_{min}, \dot{\Phi}_{min} + 1, ..., \dot{\Phi}_{max}\}Φ˙k∈{Φ˙min,Φ˙min+1,...,Φ˙max}表示第kkk个frame的tempi,Φ˙min\dot{\Phi}_{min}Φ˙min和Φ˙max\dot{\Phi}_{max}Φ˙max是人为设置的上下界。说的通俗一点,把Φk\Phi_kΦk看成位移的话,Φ˙k\dot{\Phi}_kΦ˙k就是速度,k+1k+1k+1个frame的位置Φk+1\Phi_{k + 1}Φk+1就是Φk+Φ˙k\Phi_k + \dot{\Phi}_kΦk+Φ˙k。说的音乐一点,就是Φ˙k\dot{\Phi}_kΦ˙k表示了第kkk个frame是一个几分之几的音符,比如1/8音符,如果知道这首歌是4/4拍的话,第kkk个frame就走了(1/8)/(4∗1/4)=1/8(1/8) / (4*1/4) = 1/8(1/8)/(4∗1/4)=1/8个小节(bar),这里使用离散的MMM个数值来表示了。
观测变量就是我们的frames的特征序列,记为{y1,y2,...,yK}\{\bold{y}_1, \bold{y}_2, ..., \bold{y}_K\}{y1,y2,...,yK}。我们想要找到一串隐变量的序列x1:K∗={x1∗,x2∗,...,xK∗}\bold{x}_{1:K}^*=\{\bold{x}_1^*, \bold{x}_2^*, ..., \bold{x}_K^*\}x1:K∗={x1∗,x2∗,...,xK∗}使得
x1:K∗=argmaxx1:KP(x1:K∣y1:K)(4-1)\bold{x}_{1:K}^* = arg\max_{\bold{x}_{1:K}} P(\bold{x}_{1:K} | \bold{y}_{1:K}) \tag{4-1} x1:K∗=argx1:KmaxP(x1:K∣y1:K)(4-1)
式(4−1)(4-1)(4−1)可以用viterbi算法来解,不清楚的可以参看我的搞懂HMM。求解式(4−1)(4-1)(4−1)需要知道三个模型,一个是初始概率模型P(x1)P(\bold{x}_1)P(x1),第二个是状态转移模型P(xk∣xk−1)P(\bold{x}_k|\bold{x}_{k-1})P(xk∣xk−1),第三个是发射概率P(yk∣xk)P(\bold{y}_k|\bold{x}_k)P(yk∣xk)。
(1)初始概率
初始概率P(x1)P(\bold{x}_1)P(x1),作者用了均匀分布初始化,后面用数据学就行,没啥说的。
(2)转移概率
转移概率是个比较关键的概率,我们来仔细看下
P(xk∣xk−1)=P(Φk,Φ˙k∣Φk−1,Φ˙k−1)=P(Φk∣Φ˙k,Φk−1,Φ˙k−1)P(Φ˙k∣Φk−1,Φ˙k−1)\begin{aligned} P(\bold{x}_k | \bold{x}_{k-1}) &= P(\Phi_k, \dot{\Phi}_k | \Phi_{k-1}, \dot{\Phi}_{k-1}) \\ &=P(\Phi_k | \dot{\Phi}_k, \Phi_{k-1}, \dot{\Phi}_{k-1})P(\dot{\Phi}_k | \Phi_{k-1}, \dot{\Phi}_{k-1}) \end{aligned} P(xk∣xk−1)=P(Φk,Φ˙k∣Φk−1,Φ˙k−1)=P(Φk∣Φ˙k,Φk−1,Φ˙k−1)P(Φ˙k∣Φk−1,Φ˙k−1)
我们把Φk\Phi_kΦk理解成位移,Φ˙k\dot{\Phi}_kΦ˙k理解成速度,这应该也是为啥这两个变量的符号只差了一个一阶导的符号的原因。
Φk\Phi_kΦk是kkk时刻的位置,它由上一刻的位置Φk−1\Phi_{k-1}Φk−1和上一刻的速度Φ˙k−1\dot{\Phi}_{k-1}Φ˙k−1决定,与kkk时刻的速度无关,故有
P(Φk∣Φ˙k,Φk−1,Φ˙k−1)=P(Φk∣Φk−1,Φ˙k−1)P(\Phi_k | \dot{\Phi}_k, \Phi_{k-1}, \dot{\Phi}_{k-1}) = P(\Phi_k | \Phi_{k-1}, \dot{\Phi}_{k-1}) P(Φk∣Φ˙k,Φk−1,Φ˙k−1)=P(Φk∣Φk−1,Φ˙k−1)
Φ˙k\dot{\Phi}_kΦ˙k是kkk时刻的速度,它只与k−1k-1k−1时刻的速度有关,速度不太会突变,与位置无关,故有
P(Φ˙k∣Φk−1,Φ˙k−1)=P(Φ˙k∣Φ˙k−1)P(\dot{\Phi}_k | \Phi_{k-1}, \dot{\Phi}_{k-1}) = P(\dot{\Phi}_k | \dot{\Phi}_{k-1}) P(Φ˙k∣Φk−1,Φ˙k−1)=P(Φ˙k∣Φ˙k−1)
于是有
P(xk∣xk−1)=P(Φk∣Φk−1,Φ˙k−1)P(Φ˙k∣Φ˙k−1)(4-2)P(\bold{x}_k | \bold{x}_{k-1}) = P(\Phi_k | \Phi_{k-1}, \dot{\Phi}_{k-1})P(\dot{\Phi}_k | \dot{\Phi}_{k-1}) \tag{4-2} P(xk∣xk−1)=P(Φk∣Φk−1,Φ˙k−1)P(Φ˙k∣Φ˙k−1)(4-2)
P(Φk∣Φk−1,Φ˙k−1)P(\Phi_k | \Phi_{k-1}, \dot{\Phi}_{k-1})P(Φk∣Φk−1,Φ˙k−1)就是一个位移的计算,可以定义为
P(Φk∣Φk−1,Φ˙k−1)={1,if(Φk−1+Φ˙k−1−1)%M+10,otherwise(4-3)P(\Phi_k | \Phi_{k-1}, \dot{\Phi}_{k-1}) = \begin{cases} 1, &if \ (\Phi_{k-1} + \dot{\Phi}_{k-1} - 1) \% \ M + 1\\ 0, &otherwise \end{cases} \tag{4-3} P(Φk∣Φk−1,Φ˙k−1)={1,0,if (Φk−1+Φ˙k−1−1)% M+1otherwise(4-3)
也就是Φk=(Φk−1+Φ˙k−1−1)%M+1\Phi_k = (\Phi_{k-1} + \dot{\Phi}_{k-1} - 1) \% \ M + 1Φk=(Φk−1+Φ˙k−1−1)% M+1的意思。这里取余是为了在下一个bar中,位置重新计数。为啥要先减1再取余再加1?我猜测是为了避免产生Φk=0\Phi_k=0Φk=0的情况,使得Φk\Phi_kΦk的取值在{1,2,...,M}\{1,2,...,M\}{1,2,...,M},只是为了符号的统一。
P(Φ˙k∣Φ˙k−1)P(\dot{\Phi}_k | \dot{\Phi}_{k-1})P(Φ˙k∣Φ˙k−1)是一个速度变化的概率,定义为
P(Φ˙k∣Φ˙k−1)={1−p,Φ˙k=Φ˙k−1p2,Φ˙k=Φ˙k−1+1p2,Φ˙k=Φ˙k−1−1(4-4)P(\dot{\Phi}_k | \dot{\Phi}_{k-1}) = \begin{cases} 1 - p, & \dot{\Phi}_k=\dot{\Phi}_{k-1} \\ \frac{p}{2}, & \dot{\Phi}_k=\dot{\Phi}_{k-1} + 1 \\ \frac{p}{2}, & \dot{\Phi}_k=\dot{\Phi}_{k-1} - 1 \end{cases} \tag{4-4} P(Φ˙k∣Φ˙k−1)=⎩⎪⎨⎪⎧1−p,2p,2p,Φ˙k=Φ˙k−1Φ˙k=Φ˙k−1+1Φ˙k=Φ˙k−1−1(4-4)
ppp是速度发生变化的一个概率,我们人为限制了速度只能在距离为1的速度上转移或者保持不变。在边界Φ˙min\dot{\Phi}_{min}Φ˙min和Φ˙max\dot{\Phi}_{max}Φ˙max上,略有不同,保持速度不超界即可。ppp是需要学习得到的。
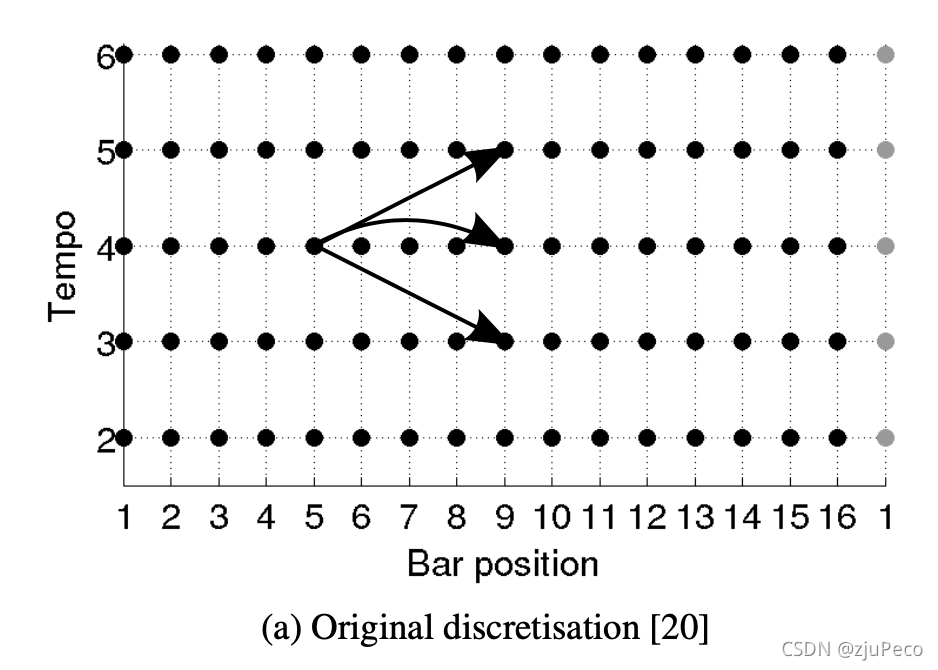
原始状态转移示意图如图4-1所示,可以很明显滴看出位置和速度的关系。
(3)发射概率
这里是结合RNN的结果的地方。我们假设第kkk个frame为beat的概率是bkb_kbk,为downbeat的概率是dkd_kdk,既不是beat也不是downbeat的概率为nkn_knk。那么发射概率就为
P(yk∣xk)={bk,sk∈Bdk,bk∈Dnkλ0−1,otherwise(4-5)P(\bold{y}_k | \bold{x}_k) = \begin{cases} b_k, &s_k \in B \\ d_k, &b_k \in D \\ \frac{n_k}{\lambda_0 - 1}, & otherwise \end{cases} \tag{4-5} P(yk∣xk)=⎩⎪⎨⎪⎧bk,dk,λ0−1nk,sk∈Bbk∈Dotherwise(4-5)
BBB表示xkx_kxk被认为是beat的集合,DDD表示xkx_kxk被认为是downbeat的集合。怎么样的xkx_kxk会被认为是beat或是downbeat呢?这点论文中没有细说,我看了A Multi-model Approach to Beat Tracking Considering Heterogeneous Music Styles中的做法,大概猜测了一下,是将位置在小节等分点附近的states作为beat或者downbeat,每个小节的第一个等分点附近为downbeat(每小节的第一拍为强拍),其他的等分点附近为beat。这个附近有多近,其实是个可以人为设置的范围。按几等份算,则是一个用户需要提前输入的参数,比如一首歌是3/4拍的,那每个小节就有3拍,就三等分,又比如一首歌是6/8拍的,那每个小节就有6拍,就六等份。如果不知道是几几拍的音乐的话,就一个个算过去,取概率最大的,这个在下一节会讲。
λ0\lambda_0λ0是个超参数,论文中取λ0=16\lambda_0=16λ0=16得到了最好的实验结果。BBB和DDD的范围和λ0\lambda_0λ0相关。
4.2 原始的bar pointer model的缺点
(1)位置(时间)分辨率
原文中说是时间分辨率,我这里直接说成位置分辨率了,这样比较方便理解。作者认为不同的速度下,需要的位置分辨率是不同的。速度快的,每次都大步大步跨,需要的位置分辨率很低;速度慢的,每次跨的步幅小,需要的位置分辨率就高了。一句话说,就是不同的速度条件下,要不同的位置分辨率。
(2)速度分辨率
原文中的tempo就是我这里的速度。作者认为人耳对于速度的变化感知,在不同的速度下是不一样。比如在速度为1的时候,速度加个1,变成2,听起来就变化很明显了。但是在速度为10的时候,速度价格1,变成11,听起来都没什么变化。也就是人耳的听觉不是linear的,而是log linear的。
(3)速度的稳定性
使用HMM时,有一个齐次马尔科夫假设,认为Φk\Phi_kΦk只依赖于Φ˙k\dot{\Phi}_kΦ˙k,这可能会导致同一个beat里,速度经过几个frames之后就产生比较大的变化,也就是速度的稳定性无法保证。
4.3 改进后的模型
论文针对4.2中提出的三点对模型进行了改进,改进都是针对状态转移的计算的。改进后的状态转移示意图,如下图4-2所示。
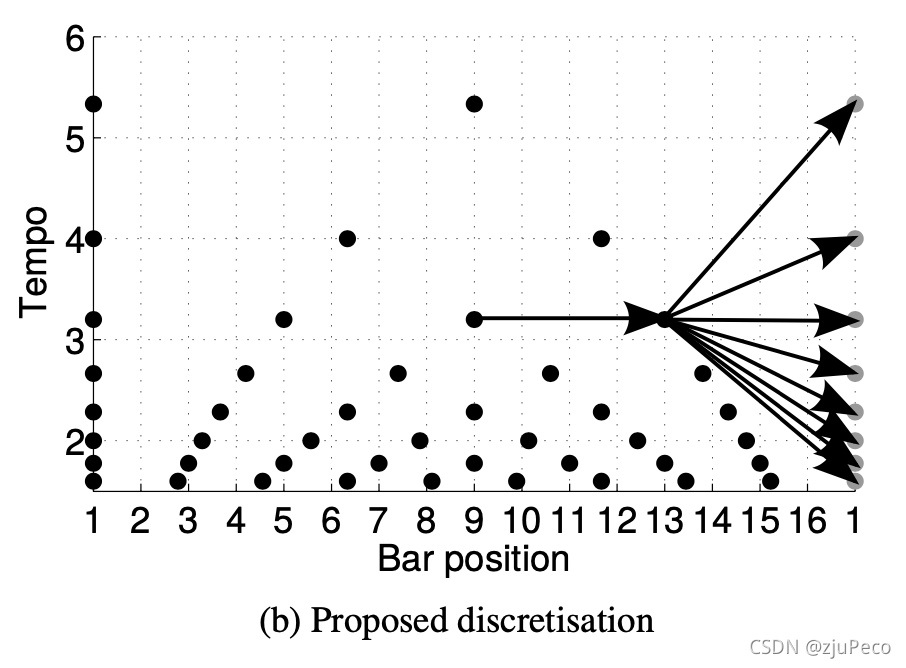
(1)位置分辨率的改进
这里说白了就是根据速度来调整一个bar要被分成几份。从图4-2中的横向可以看出,tempo越大的,bar position就被分的越稀疏,反之越密。划分方式我们从具体madmom的实现来看,不看论文里说的,论文里说的有些模糊。
"""
max_bpm:用户输入,表示最大的beats per minute,默认为215
min_bpm:用户输入,表示最小的beats per minute,默认为55
fps:用户输入,frame per secondmin_interval:计算得到,最小的frame per beat
max_interval:计算得到,最大的frame per beat
"""
# convert timing information to construct a beat state space
min_interval = 60. * fps / max_bpm # second per beat * frame per second = frame per beat
max_interval = 60. * fps / min_bpm
上面代码片中的min_interval和max_interval就是由最大的bpm和最小的bpm确定的每个beat被分为多少个frames。一个bar有多少个beats也是用户输入的,所以一个bar的bar positions也就根据速度的不同确定了。
(2)速度分辨率的改进
速度在min_bpm和max_bpm的范围内,按log linear的方式进行了划分。具体的实现可以看这一段https://github.com/CPJKU/madmom/blob/master/madmom/features/beats_hmm.py#L66。应该说实现中,没有速度这个东西,都转变成了位置。不同bpm下有不同的位置点,log linear的对象是位置。
(3)速度稳定性
作者为了保证速度的稳定性,速度只能在每个beat的位置上发生改变,改变时依赖于一个分布,这个分布是在实验中试了几个得到的。
当Φk∈B\Phi_k \in BΦk∈B时
P(Φ˙k∣Φ˙k−1)=f(Φ˙k,Φ˙k−1)(4-6)P(\dot{\Phi}_k | \dot{\Phi}_{k-1}) = f(\dot{\Phi}_k, \dot{\Phi}_{k-1}) \tag{4-6} P(Φ˙k∣Φ˙k−1)=f(Φ˙k,Φ˙k−1)(4-6)
其中f(Φ˙k,Φ˙k−1)f(\dot{\Phi}_k, \dot{\Phi}_{k-1})f(Φ˙k,Φ˙k−1)可以是各种各样的函数,效果比较好的是
f(Φ˙k,Φ˙k−1)=exp(−λ×∣Φ˙kΦ˙k−1−1∣)(4-7)f(\dot{\Phi}_k, \dot{\Phi}_{k-1}) = exp(-\lambda \times |\frac{\dot{\Phi}_k}{\dot{\Phi}_{k-1}} - 1|) \tag{4-7} f(Φ˙k,Φ˙k−1)=exp(−λ×∣Φ˙k−1Φ˙k−1∣)(4-7)
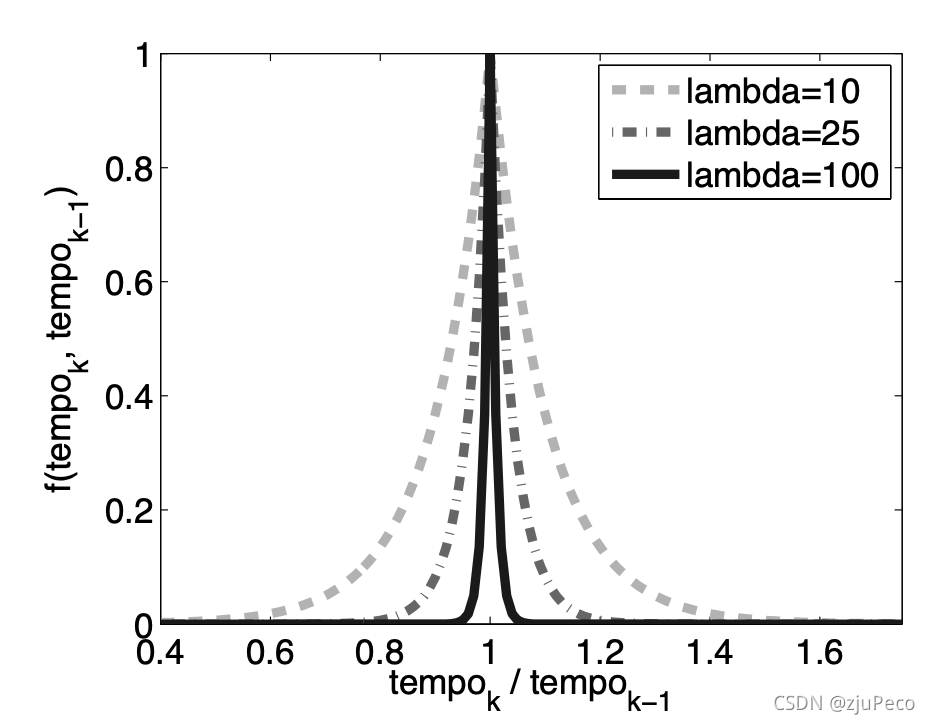
不难看出,当Φ˙k−1=Φ˙k\dot{\Phi}_{k-1} = \dot{\Phi}_kΦ˙k−1=Φ˙k时概率最大。λ∈[1,300]\lambda \in [1, 300]λ∈[1,300]是一个超参数,不同λ\lambdaλ下f(Φ˙k,Φ˙k−1)f(\dot{\Phi}_k, \dot{\Phi}_{k-1})f(Φ˙k,Φ˙k−1)的结果如下图4-3所示。
当Φk∉B\Phi_k \notin BΦk∈/B时
P(Φ˙k∣Φ˙k−1)={1,Φ˙k=Φ˙k−10,otherwise(4-8)P(\dot{\Phi}_k | \dot{\Phi}_{k-1}) = \begin{cases} 1, & \dot{\Phi}_k = \dot{\Phi}_{k-1} \\ 0, & otherwise \end{cases} \tag{4-8} P(Φ˙k∣Φ˙k−1)={1,0,Φ˙k=Φ˙k−1otherwise(4-8)
表示速度不变。
5 预测
madmom很清晰地把整个模型分成了两块,DBNDownBeatTrackingProcessor和RNNDownBeatProcessor。RNNDownBeatProcessor就是我们的RNN网络,DBNDownBeatTrackingProcessor是HMM的部分。从宏观上讲,beats和downbeats的位置是由RNN大致确定,然后由HMM根据周期性这个条件去决定最后的位置的。RNN可以理解为是针对局部的理解,HMM是针对全局的决策。
在预测的时候,我们会告诉模型这首歌每个bar的beat有几个,如果不确定的话,就把beats_per_bar=[2,3,4,6]全填上,让模型每个跑一边,然后取概率最大的就行了。
在每个beats_per_bar下,我们算一个最佳的隐变量路径
x1:K∗=argmaxx1:K(x1:K∣y1:K)(5-1)\bold{x}_{1:K}^* = arg\max_{x_{1:K}}(\bold{x}_{1:K} | \bold{y}_{1:K}) \tag{5-1} x1:K∗=argx1:Kmax(x1:K∣y1:K)(5-1)
解这个用viterbi算法就可以了。
最终的结果就是
B∗={k:xk∗∈B}(5-2)B^* = \{k : \bold{x}_k^* \in B\} \tag{5-2} B∗={k:xk∗∈B}(5-2)
D∗={k:xk∗∈D}(5-2)D^* = \{k : \bold{x}_k^* \in D\} \tag{5-2} D∗={k:xk∗∈D}(5-2)
确定了B∗B^*B∗和D∗D^*D∗之后,还会根据RNN的结果,把点修正到附近的概率峰值点上。
验证模型的时候,把误差在70ms以内的点都认为是正确的。madmom的效果还是很不错的。
参考资料
[1] madmom implementation
[2] Joint Beat and Downbeat Tracking with Recurrent Neural Networks
[3] An Efficient State-Space Model for Joint Tempo and Meter Tracking
[4] 百度百科-音乐节拍
[5] Bayesian Modelling of Temporal Structure in Musical Audio
[6] A Multi-model Approach to Beat Tracking Considering Heterogeneous Music Styles



)



)











