1 概述

Vision Transformer是transformer应用到图像领域的一个里程碑，它将CNN完全剔除，只使用了transformer来完成网络的搭建，并且在图像分类任务中取得了state-of-art的效果。

Swin Transformer则更进一步，引入了一些inductive biases，将CNN的结构和transformer结合在了一起，使得transformer在图像全领域都取得了state of art的效果。Swin Transformer中也有用到CNN，但是并不是把CNN当做CNN来用的，只是用CNN的模块来写代码比较方便。所以，也可以认为是完全没有使用CNN。

网上关于Swin Transformer的解读多的不得了，这里来说说Swin Transformer在视频领域的应用，也就是Video Swin Transformer。如果非常熟悉Swin Transformer的话，那这篇文章就非常容易读懂了，只是多了一个时间的维度，做attention和构建window的时候略有区别。本文的参考资料也大多是Swin Transformer的。

这篇文章会从视频的角度来解读Swin Transformer。

2 模型介绍

2.1 整体架构

2.1.1 backbone

Video Swin Transformer的backbone的整体架构和Swin Transformer大同小异，多了一个时间维度$T$，在做Patch Partition的时候会有个时间维度的patch size。

图2-1 tiny video swin tranformer架构

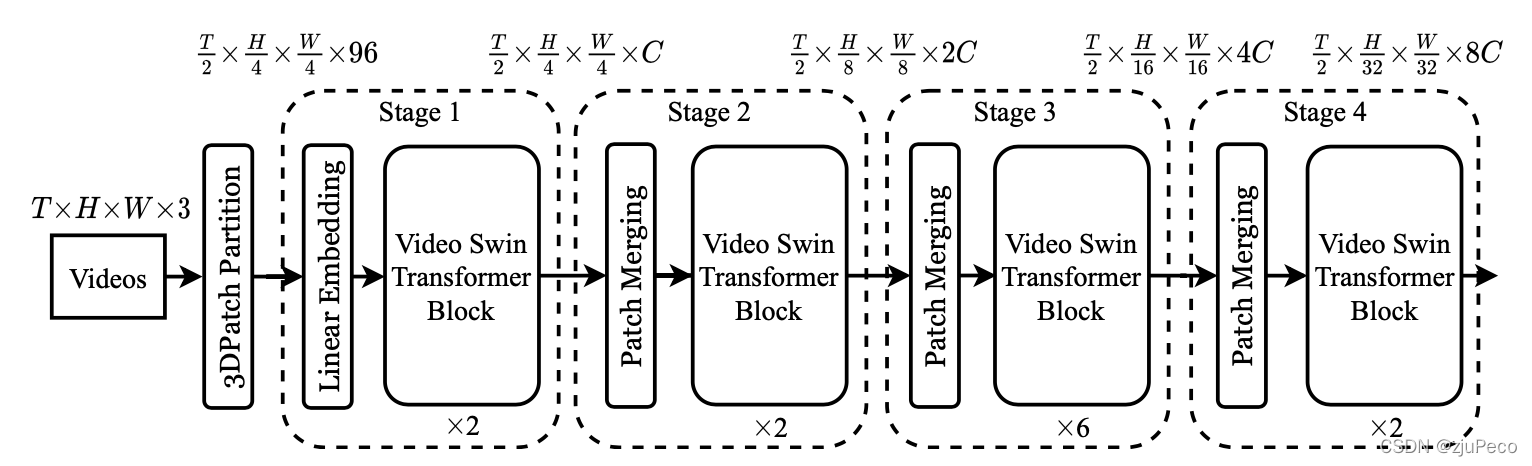
以图2-1为例，输入为一个尺寸为$T\times H\times W\times 3$的视频，通常还会有个batch size，这里省略掉了。$T$一般设置为32，表示从视频的所有帧中采样得到32帧，采样的方法可以自行选择，不同任务可能会有不同的采样方法，一般为等间隔采样。这里其实也就天然限制了模型不能处理和训练数据时长相差太多的视频。通常视频分类任务的视频会在10s左右，太长的视频也很难分到一个类别里。

输入经过Patch Partition之后会变成一个$\frac{T}{2}\times \frac{H}{4}\times \frac{W}{4}\times 96$的向量。这是因为patch size在这里为$(2,4,4)$，分别是时间，高度和宽度三个维度的尺寸，其中$96$是因为$2\times 4\times 4\times 3=96$，也就是一个patch内的所有像素点的rgb三个通道的值。Patch Partition会在2.2中详述。

Patch Partiion之后会紧跟一个Linear Embedding，这两个模块在代码中是写在一起的，可以参见PatchEmbed3D，就是直接用一个3D的卷积，用这个卷积充当全连接。如果embedding的dim为96，那么经过embedding之后的尺寸还是$2\times 4\times 4\times 3=96$。

之后分别会经过多个video swin transformer block和patch merging。video swin transformer是利用attention同一个window内的特征进行特征融合的模块；patch merging则是用来改变特征的shape，可以当作CNN模型当中的pooling，不过规则不同，而且patch merging还会改变特征的dim，也就是$C$改变。整个过程模仿了CNN模块中的下采样过程，这也是为了让模型可以针对不同尺度生成特征。浅层可以看到小物体，深层则着重关注大物体。

video swin transformer block的结构如下图2-2所示。

图2-2 video swin transformer block结构

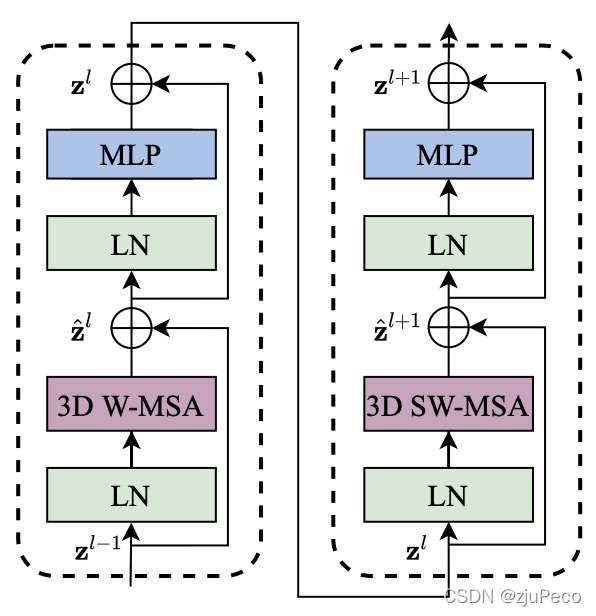
图2-2的左和右是两个不同的blocks，需要连在一起搭配使用。在图2-1中的video swin tranformer block下方有$\times 2$或是$\times 6$这样的符号，表示有几个blocks，这必定是个偶数，比如$\times 2$就表示图2-2这样1组blocks，$\times 6$就表示图2-2这样3组blocks相连。

不难看出，有两种blocks，每个block都是先过一个LN(LayerNorm)，再过一个MSA(multi-head self-attention)，再过一个LN，最后过一个MLP(multilayer perceptron)，其中有两处使用了残差模块。残差块主要是为了缓解梯度弥散。

两种blocks的区别在于前者的MSA是window MSA，后者是shifted-window MSA。前者是为了window内的信息交流（局部），后者是为了window间的信息交流（全局）。这个会在2.2中进行详述。

2.1.2 head

backbone的作用是提取视频的特征，真正来做分类的还是接在backbone后面的head，这个部分就很简单了，就是一层全连接，代码中使用的是I3DHead。顺便还带了AdaptiveAvgPool3d，这是用来将输入变成适合全连接的shape的。这部分就不说了，没啥说的。

2.2 模块详述

2.2.1 Patch Partition

下图2-3是一段视频中的8帧，每帧都被分成了$8\times 8=64$个网格，假设每个网格的像素为$4\times 4$，那么当patch size为$(1,4,4)$时，每个小网格就是一个patch；当patch size为$(2,4,4)$时，每相邻两帧的同一个位置的网格组成一个patch。这里和vision tranformer中的划分方式相同，只不过多了时间的概念。

图2-3 Patch Partition示意图

2.2.2 3D Patch Merging

3D Patch Merging这一块直接看代码会比较好理解，它和swin transformer中的2D patch merging一模一样，3D Patch Merging虽然多了时间维度，但是并没有对时间维度做merging的操作，也就是输出的时间维度不变。

x0 = x[:, :, 0::2, 0::2, :]  # B T H/2 W/2 C
x1 = x[:, :, 1::2, 0::2, :]  # B T H/2 W/2 C
x2 = x[:, :, 0::2, 1::2, :]  # B T H/2 W/2 C
x3 = x[:, :, 1::2, 1::2, :]  # B T H/2 W/2 C
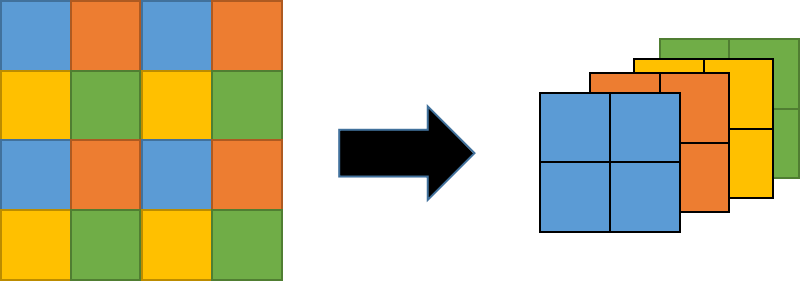
x = torch.cat([x0, x1, x2, x3], -1)  # B T H/2 W/2 4*C

看代码再结合图就更好理解了。图中每个颜色都是一个patch。

图2-4 Patch Merging示意图

2.2.3 W-MSA

MSA(multihead self attention)的原理这里就不说了，不懂的可以参见搞懂Transformer，这里主要来说一说这个window。W-MSA(window based MSA)相比于MSA多了一个window的概念，相比于vision transformer引入window的目的是减小计算复杂度，使得复杂度和输入图片的尺寸成线性关系。这里不推导复杂度的计算，有兴趣的可以看Swin Transformer论文精读，这里有很详细的推导，3D和2D的复杂度计算方法是一致的。

图2-5 W-MSA示意图

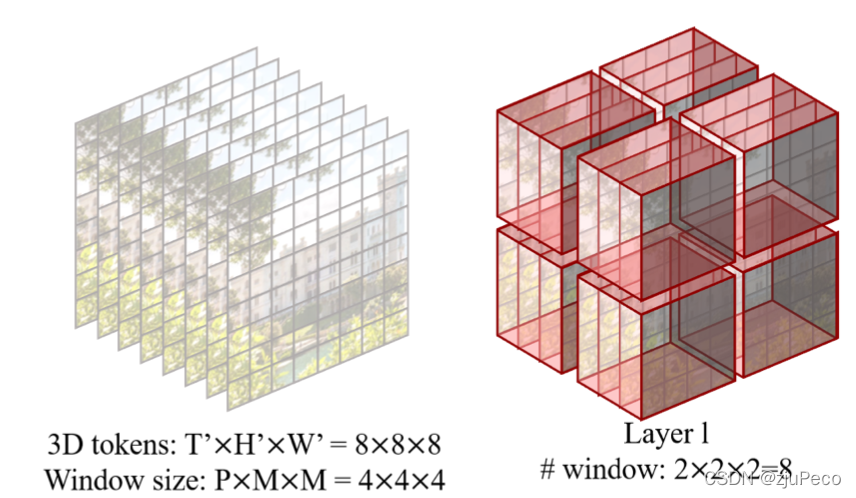
窗口的划分方式如图2-5所示，每个窗口的大小由window size决定。图2-5的window size为$(4,4,4)$就表示在时间，高度和宽度的window尺寸都是4个patch，划分后的结果如图2-5右半所示。之后的attention每个window单独做，window之间不互相干扰。

2.2.4 SW-MSA

由于W-MSA的attention是局部的，作者就提出了SW-MSA(shifted window based MSA)。

图2-6 SW-MSA示意图

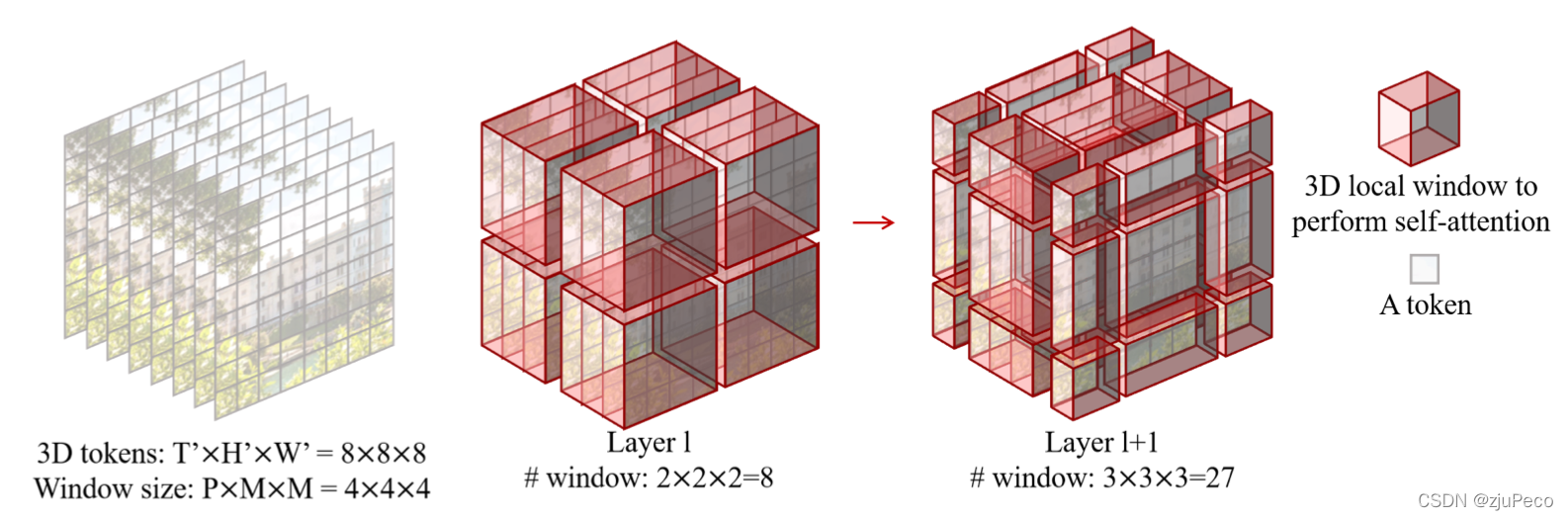
SW-MSA如图2-6所示，图中shift size为$(2,2,2)$，一般shift size都是window size的一半，也就是$(\frac{P}{2},\frac{M}{2},\frac{M}{2})$。shift了之后，window会往前，往右，往下分别移动对应的size，目的是让patch可以和不同window的patch做特征的融合，这样多过几层之后，也就相当于做了全局的特征融合。

不过这里有一个问题，shift了之后，window的数量从原来的$2\times 2\times 2=8$变成了$3\times 3\times 3=27$。这带来的弊端就是计算时窗口不统一会比较麻烦。为了解决这个问题，作者引入了mask，并将窗口的位置进行了移动，使得进行shift和不进行shift的MSA计算方式相同，只不过mask不同。

图2-7 shift window示意图

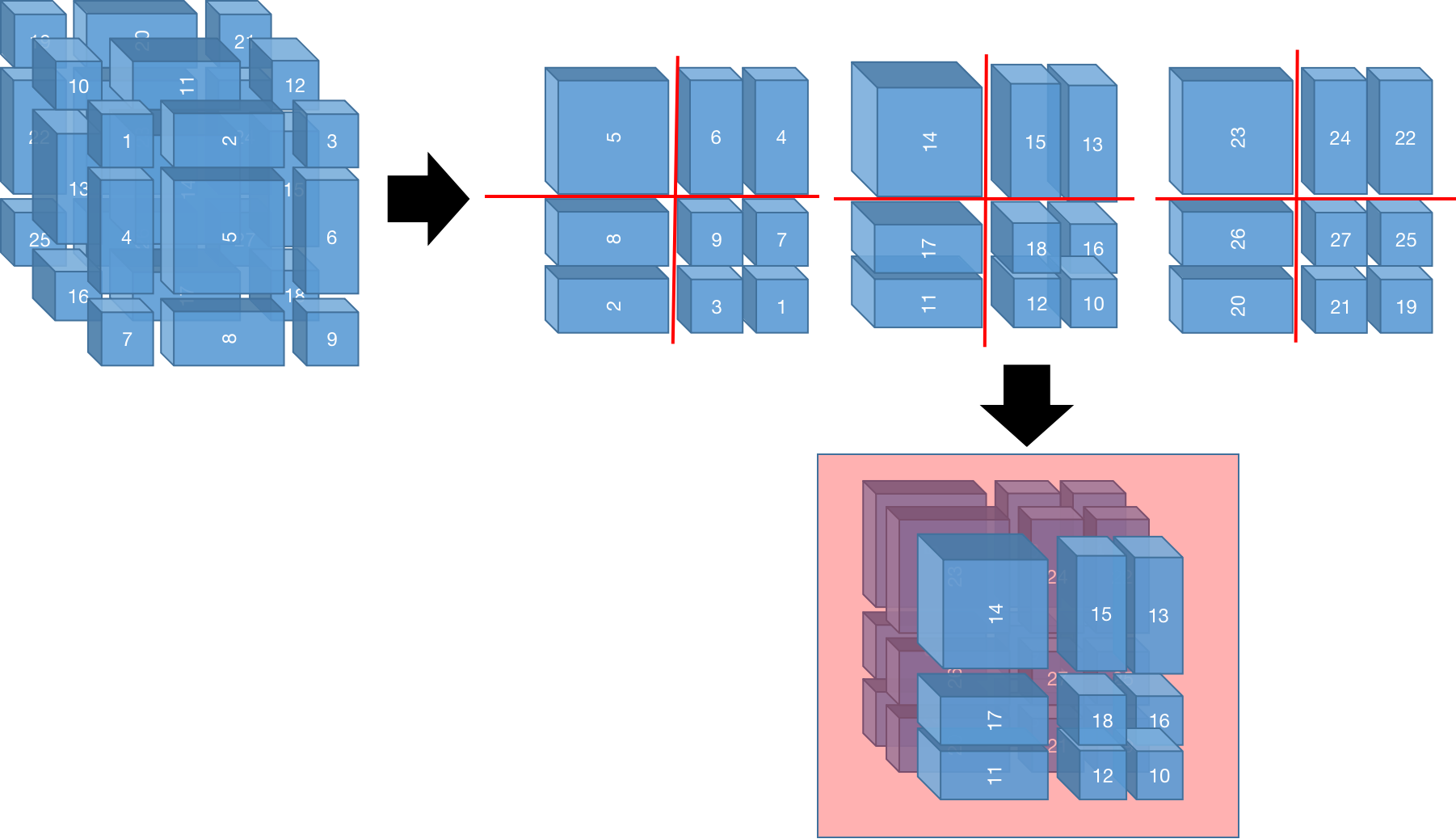
我用PPT画了一下shift的过程，画图能力有限，能看懂就好。我们的目的是把图2-6中最右侧的27个windows变成和图2-6中间那样的8个window。我给每个window都标了序号，标序号的方式是从前往后，从上往下，从左往右。shift window的方法就是把左上角的移到右下角，把前面的移到后面。这样一来，比如$[27,25,21,19,9,7,3,1]$就组成了1个window，$[18,16,12,10]$就组成了1个window，依此类推，一共有8个windows。平移的方式可以和上述的不同，只要保证可以把27个windows变成和8个windows的计算方式一样即可。

这样在每个window做self-attention的时候，需要加一层mask，可以说是引入了inductive bias。因为在组合而成的window内，各个小window我们不希望他们交换信息，因为这不是图像原有的位置，比如17和11经过shift之后，会在同一个window内做attention，但是11是从上面移下来的，只是为了计算的统一，并不是物理意义上的同一个window。有了mask就不一样了，mask的目的是告诉17号窗口内的每一个patch，只和17号窗口内的patches做attention，不和11号窗口内的做attention，依此类推其他。

mask的生成方法可以参见源码，这里不细讲，主要思路是就像图2-7这样，给每个patch一个window的编号，编号相同的patch之间mask为0，否则为-100。

def compute_mask(D, H, W, window_size, shift_size, device):img_mask = torch.zeros((1, D, H, W, 1), device=device)  # 1 Dp Hp Wp 1cnt = 0for d in slice(-window_size[0]), slice(-window_size[0], -shift_size[0]), slice(-shift_size[0],None):for h in slice(-window_size[1]), slice(-window_size[1], -shift_size[1]), slice(-shift_size[1],None):for w in slice(-window_size[2]), slice(-window_size[2], -shift_size[2]), slice(-shift_size[2],None):img_mask[:, d, h, w, :] = cntcnt += 1mask_windows = window_partition(img_mask, window_size)  # nW, ws[0]*ws[1]*ws[2], 1mask_windows = mask_windows.squeeze(-1)  # nW, ws[0]*ws[1]*ws[2]attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))return attn_mask

如果window的大小为图2-6中的$(P,M,M)$的话，attention mask就是一个$(P\times M\times M，P\times M\times M)$的矩阵，这是一个对称矩阵，第$i$行第$j$列就表示window中的第$i$个patch和第$j$个patch的window编号是否是相同的，相同则为0，不同则为-100。对角线上的元素必为0。

有人认为浅层的网络需要SW-MSA，深层的就不需要了，因为浅层已经讲全局的信息都交流了，深层不需要进一步交流了。这种说法的确有一定的道理，但也要看网络的深度和shift的尺寸。

2.2.5 Relative Position Bias

在上述的所有内容中，都没有涉及到位置的概念，也就是模型并不知道每个patch在图片中和其他patches的位置关系是怎么样的，最有也就是知道某几个patch是在同一个window内的，但window内的具体位置也是不知道的，因此就有了Relative Position Bias。它是加在attention的部分的，下式$(2-1)$中的$B$就是Relative Position Bias。

$$Attention(Q,K,V)=Softmax(Q{K}^T/\sqrt{d}+B)V\text{\hspace{1em}(2-1)}$$

很多swin tranformer的文章都会将这个$B$是如何得到的，但是却没有讲为什么要这样生成$B$。其实只要知道了设计这个$B$的目的，就可以不用管是如何生成的了，甚至自己设计一种生成的方法都行。

$B$是为了表示一个windows内，每个patch的相对位置，给每个相对位置一个特殊的embedding值。其实也正是因为这个$B$的存在，SW-MSA才必须要有mask，因为SW-MSA内的patches可能来自于多个windows，相对位置不能按照这个方法给，如果$B$可以表示全图的相对位置，那就不用这个mask了。

这个B和mask的shape是一致的，也是$(P\times M\times M，P\times M\times M)$的矩阵，第$i$行第$j$列就表示window中的第$j$个patch相对于第$i$个patch的位置。

下图2-8是我画的一个示意图，即使是一个$(2,2,2)$的window，我也感到工作量太大，矩阵没填满，画了几个示意了一下。如果window size为$(P,M,M)$的话，那么相对位置状态就会有$(2P-1)\times (2M-1)\times (2M-1)$种状态，我把$(2,2,2)$的window的27种相对位置状态全都在图2-8上写出来了。

图2-8 Relative Position Bias示意图

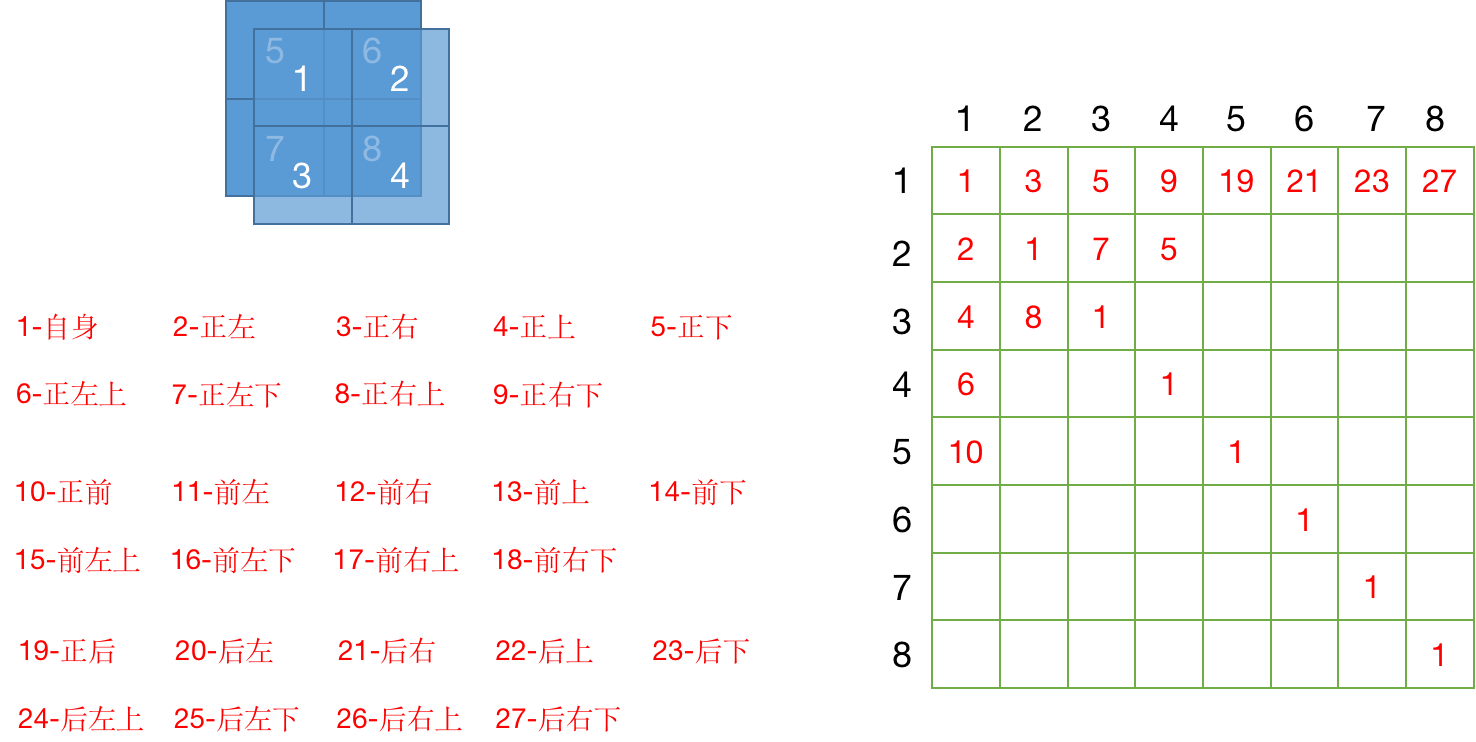
有了状态之后，就只需要在$B$这个矩阵中将相对位置的状态对号入座即可。这就是很多其他博客写的相对位置坐标相减，然后加个偏置，再乘个系数的地方。理解了为什么要这么做，看那些操作也就不会觉得奇怪了。

但最终使用的不是状态，而是状态对应的embedding值，这就需要有一个table来根据状态查找embedding，这个embedding是模型训练出来的。

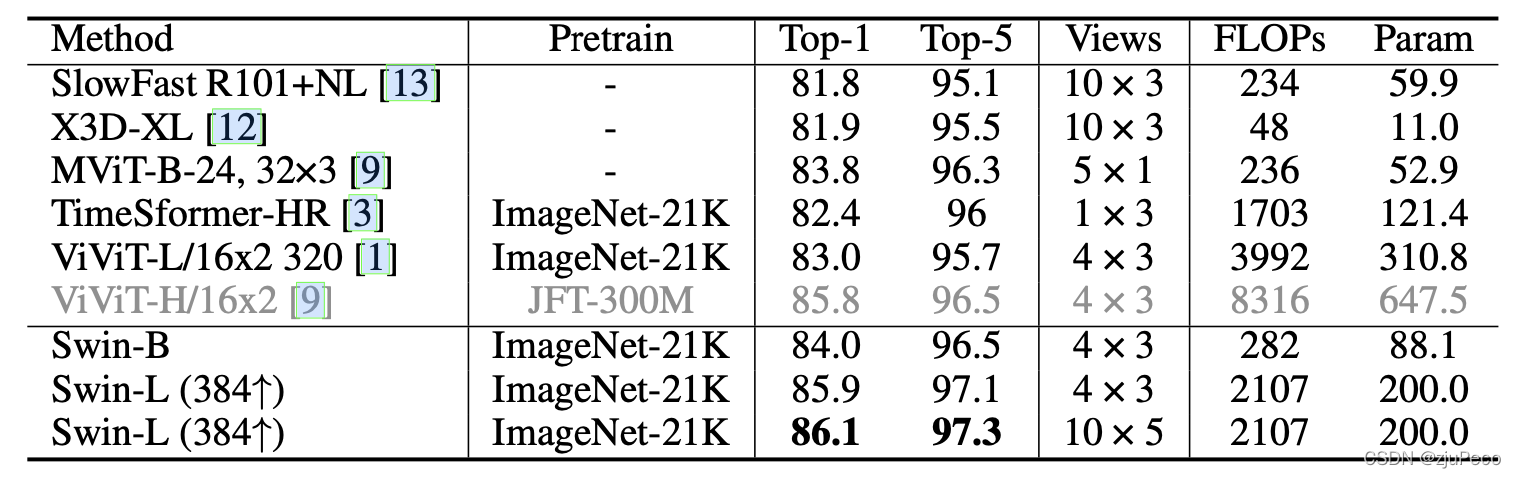
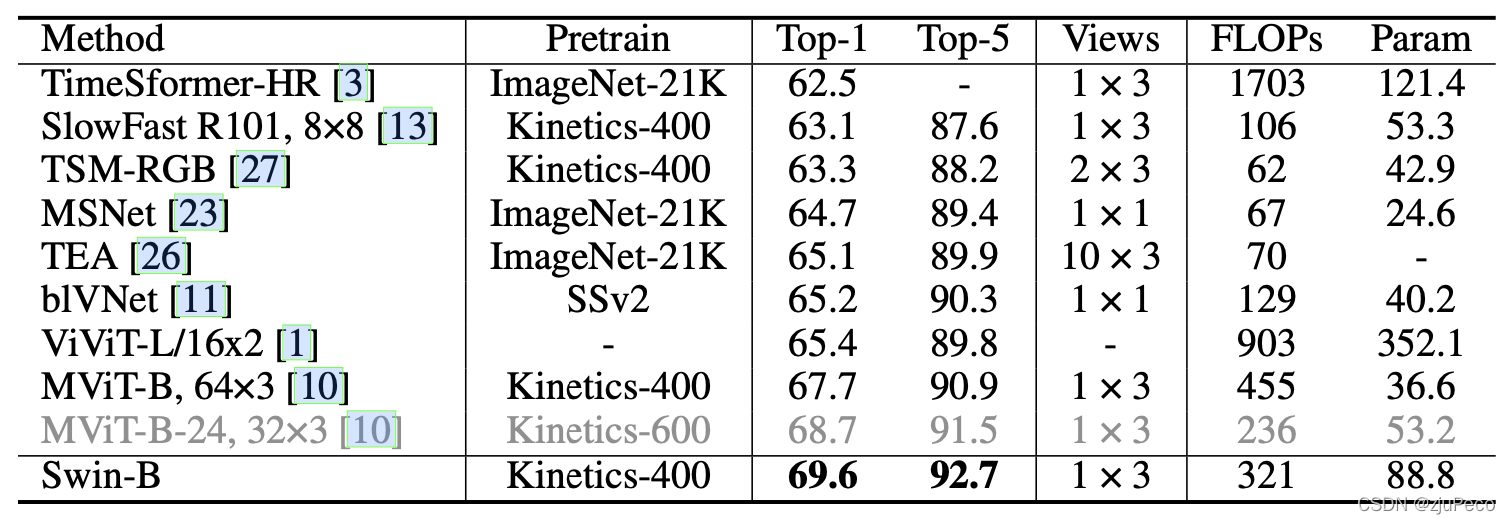
3 模型效果

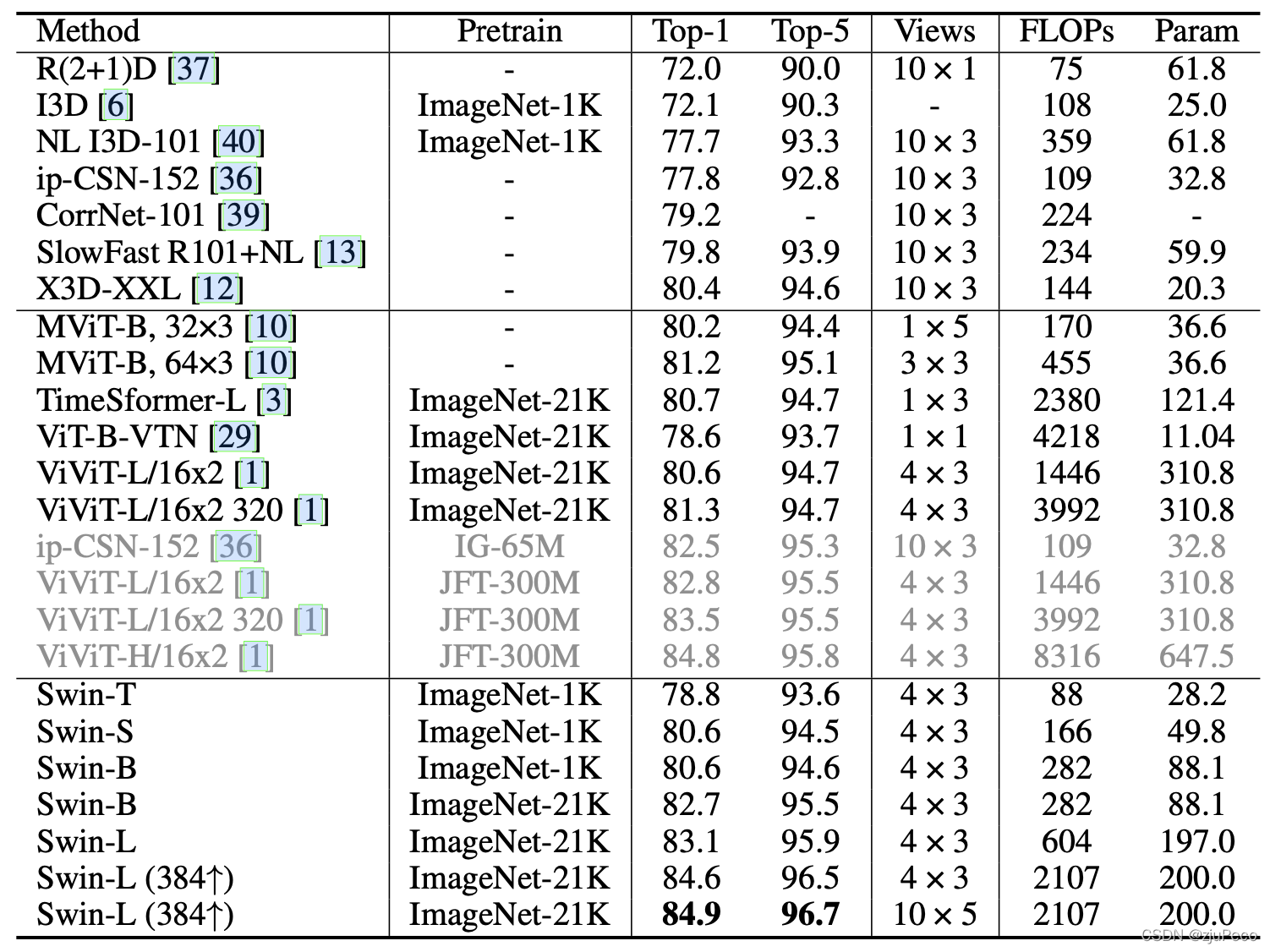
作者在三个数据集上进行了测试，分别是kinetics-400，kinetics-600和something-something v2。每个数据集上都有着state-of-art的表现。

表3-1 kinetics-400模型对比指标

表3-2 kinetics-600模型对比指标

表3-3 something-something v2模型对比指标

参考资料

[1] Video Swin Transformer
[2] Swin-Transformer网络结构详解
[3] Swin Transformer论文精读
[4] Swin Transformer从零详细解读
[5] https://github.com/SwinTransformer/Video-Swin-Transformer