2.1 线性回归算法模型表示

让我们通过一个例子来开始：这个例子是预测住房价格的，我们要使用一个数据集，数据集包含俄勒冈州波特兰市的住房价格。在这里，我要根据不同房屋尺寸所售出的价格，画出我的数据集。比方说，如果你朋友的房子是1250平方尺大小，你要告诉他们这房子能卖多少钱。那么，你可以做的一件事就是构建一个模型，也许是条直线，从这个数据模型上来看，也许你可以告诉你的朋友，他能以大约220000(美元)左右的价格卖掉这个房子。这就是监督学习算法的一个例子。

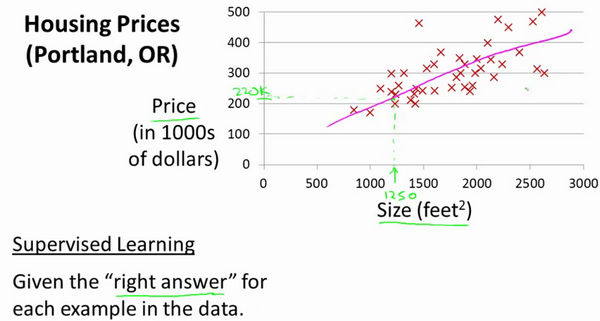
它被称作监督学习是因为对于每个数据来说，我们给出了“正确的答案”，即告诉我们：根据我们的数据来说，房子实际的价格是多少，这是一个回归问题。回归指的是，我们根据之前的数据预测出一个准确的输出值，对于这个例子就是价格，同时，还有另一种最常见的监督学习方式，叫做分类问题，当我们想要预测离散的输出值，例如，我们正在寻找癌症肿瘤，并想要确定肿瘤是良性的还是恶性的，这就是0/1离散输出的问题。

更进一步来说，在监督学习中我们有一个数据集，这个数据集被称训练集。

我将在整个课程中用小写的来表示训练样本的数目。

以之前的房屋交易问题为例，假使我们回归问题的训练集（Training Set）如下表所示：

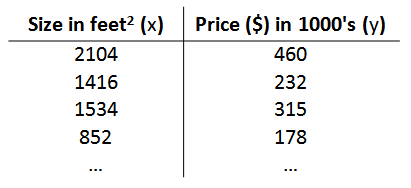
我们将要用来描述这个回归问题的标记如下:

m 代表训练集中实例的数量

 x 代表特征/输入变量

 y 代表目标变量/输出变量

 (x,y)代表训练集中的实例

 (x(i),y(i))代表第i个观察实例

 h代表学习算法的解决方案或函数也称为假设（hypothesis）

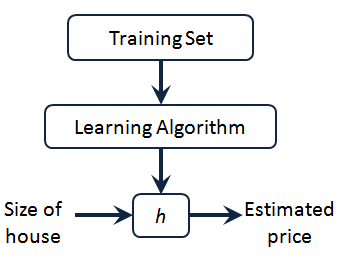
监督学习算法的工作方式，通过将数据集中的训练集传入线性模型算法中，即可输出一个

我们可以看到这里有我们的训练集里房屋价格 我们把它喂给我们的学习算法，学习算法的工作了，然后输出一个函数，通常表示为小写 h表示。 代表hypothesis(假设)，表示一个函数，输入是房屋尺寸大小，就像你朋友想出售的房屋，因此 h根据输入的x值来得出y值，y值对应房子的价格 因此，h是一个从x到y的函数映射。

我将选择最初的使用规则代表hypothesis，因而，要解决房价预测问题，我们实际上是要将训练集“喂”给我们的学习算法，进而学习得到一个假设，然后将我们要预测的房屋的尺寸作为输入变量输入给，预测出该房屋的交易价格作为输出变量输出为结果。那么，对于我们的房价预测问题，我们该如何表达 ？

一种可能的表达方式为：

因为只含有一个特征/输入变量，因此这样的问题叫作单变量线性回归问题。

2.2 代价函数

代价函数的概念有助于理解如何把最有可能的直线与数据相拟合。

如图：

在线性回归中我们有一个像这样的训练集，代表了训练样本的数量，比如 m=47。而我们的假设函数，也就是用来进行预测的函数，是这样的线性函数形式：

接下来我们会引入一些术语我们现在要做的便是为我们的模型选择合适的参数θ0和θ1 ，在房价问题这个例子中便是直线的斜率和在y轴上的截距。

我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度，模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指）就是建模误差（modeling error）。

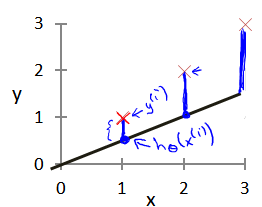
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价函数

 最小。

我们绘制一个等高线图，三个坐标分别为和θ0、θ1和J(θ0,θ1)：

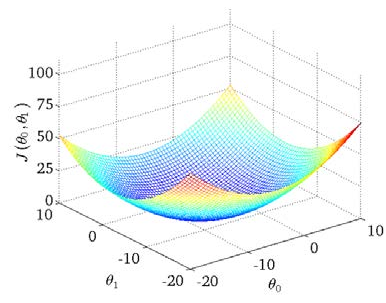
则可以看出在三维空间中存在一个使得J(θ0,θ1)最小的点。

代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题，都是一个合理的选择。还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用的手段了。

---

通过穷举法实现实现寻找最低点or最小误差

数据集设计

问题：如图一某校学生在A课程中每周投入时间y与最终成绩的数值x，因此设y=wx，设计算法求w的权重的最佳拟合数值。 

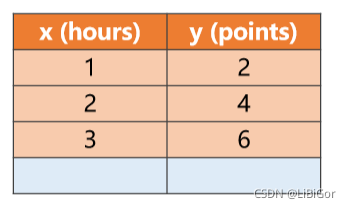
 代码：

import numpy as np
import matplotlib.pyplot as plt#数据集
x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]#构建 y = w * x ===>预测值
def forward(x):return x*w#计算loss 即 loss 公式如上图，预测值减去原始数据求误差
def loss(x,y):y_pred=forward(x)return (y_pred-y)*(y_pred-y)
#权重w的列表
w_list=[]
#损失loss的列表
mse_list=[]#对w使用穷举法，计算机y=w*x的最佳拟合值
for w in np.arange(0.0,4.1,0.1):print(w)l_sum=0#zip()当传递参数长度不一样时候，以短的为标准for x_val,y_val in zip(x_data,y_data):#计算新的预测值y_pred_val=forward(x_val)#新预测值与loss_val=loss(x_val,y_val)l_sum= l_sum+loss_valprint(x_val,y_val,y_pred_val,loss_val)#除以样本数，即平均误差MSR=l_sum/3w_list.append(w)mse_list.append(MSR)
#绘制损失loss与权重w之间的函数图像
plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

运行结果：可知当w为2时loss的损失最小

---

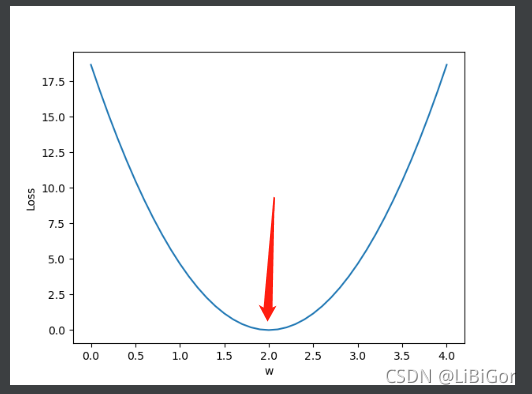
问题2

作业题目：实现线性模型（y=wx+b）并输出loss的3D图像。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D#数据集
x_data = [1.0,2.0,3.0]
y_data = [5.0,8.0,11.0]# 数据集长度
m=len(x_data)# 权值
W=np.arange(0.0,4.0,0.1)
B=np.arange(-2.0,2.0,0.1)
[w,b]=np.meshgrid(W,B)
#即三维坐标下 W做X周 B做Y周，在绘图时候一定要用小写，因为小写是N×N的二维数组，大写是一维N个数组成的数组# 注意矩阵的运算
def farword(x):return x * w+bdef loss(y_test,y):return (y_test-y)*(y_test-y)total_loss = 0
for x_val,y_val in zip(x_data,y_data):y_test=farword(x_val)total_loss=(total_loss+loss(y_test,y_val))/mfig = plt.figure()# MatplotlibDeprecationWarning: Calling gca() with keyword arguments was deprecated in Matplotlib 3.4. Starting two minor releases later, gca() will take no keyword arguments. The gca() function should only be used to get the current axes, or if no axes exist, create new axes with default keyword arguments. To create a new axes with non-default arguments, use plt.axes() or plt.subplot().
# ax = fig.gca(projection='3d') 改为
# ax = fig.add_subplot(projection='3d')
ax = Axes3D(fig)print(W.shape) #(40,)
print(W)
print(w.shape)#(40,40)
print(w)# ax.plot_surface(W,B,total_loss)
ax.plot_surface(w,b,total_loss)
plt.show()

效果图

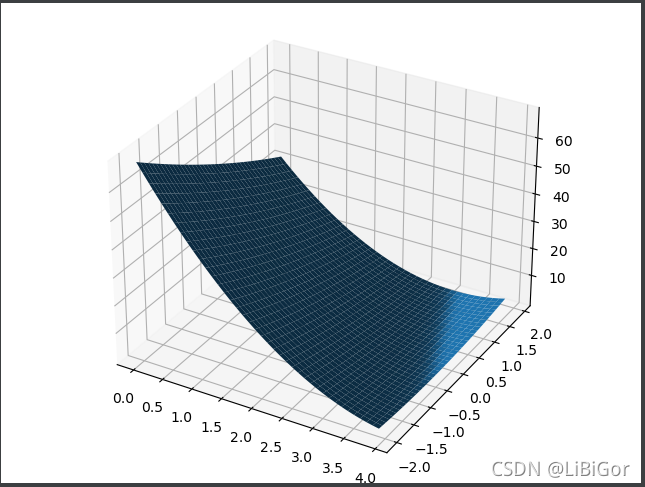
 numpy.meshgrid()理解

numpy.meshgrid()理解_lllxxq141592654的博客-CSDN博客https://blog.csdn.net/lllxxq141592654/article/details/81532855