无向图的深度优先遍历非递归_LeetCode0429: N叉树的层序遍历

题目介绍

描述：

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

例如，给定一个 3叉树 :

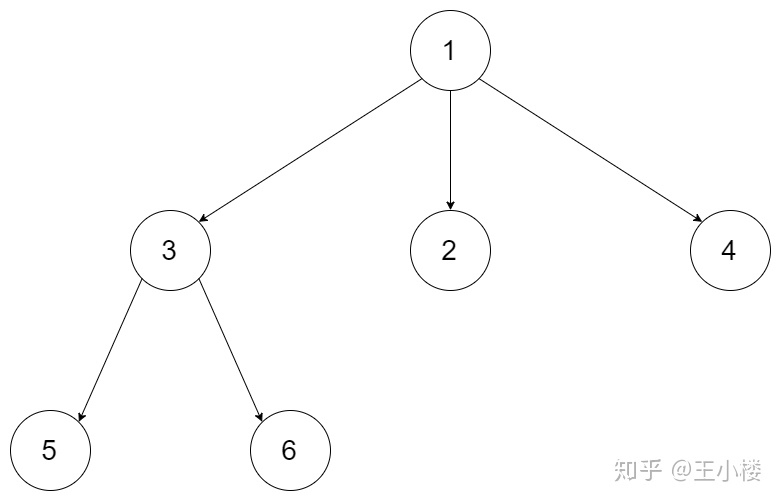
返回其层序遍历:[[1],[3,2,4],[5,6]
]说明:树的深度不会超过 1000。
树的节点总数不会超过 5000。

解题思路：

★ 递归算法的关键是要明确函数的「定义」是什么，然后相信这个定义，利用这个定义推导最终结果。
”
★ 写树相关的算法，简单说就是，先搞清楚当前 root 节点该做什么，然后根据函数定义递归调用子节点，递归调用会让孩子节点做相同的事情。
”
★ 二叉树题目的一个难点在于如何通过题目的要求思考出每一个节点需要做什么
”

二叉树解题策略

一递归二队列 + 迭代（层次遍历）三栈 + 迭代（非递归遍历）四其它

三种基本的遍历方式，都可以用递归来实现。写递归算法的时候，需要注意递归退出条件以及递归操作的表达。

自己的解法实现

def levelOrder4(self, root):from collections import dequeif not root: return []queue, res = deque([(root)]), []while queue:level = []for _ in range(len(queue)):node = queue.popleft()level.append(node.val)if node.children:queue.extend(node.children)res.append(level)return res

网上比较优秀的解法

解法一

方法一：利用队列实现广度优先搜索我们要构造一个 sub-lists 列表，其中每个 sub-list 是树中一行的值。行应该按从上到下的顺序排列。

因为我们从根节点开始遍历树，然后向下搜索最接近根节点的节点，这是广度优先搜索。我们使用队列来进行广度优先搜索，队列具有先进先出的特性。

在这里使用栈是错误的选择，栈应用于深度优先搜索。用一个列表存放节点值，队列存放节点。首先将根节点放到队列中，当队列不为空时，则在队列取出一个节点，并将其子节点添加到队列中。

def levelOrder(self, root):from collections import dequeif not root: return []queue = deque([(root)])res = []while queue:level = []for _ in range(len(queue)):node = queue.popleft()level.append(node.val)queue.extend(node.children)res.append(level)return res

解法二

广度优先

def levelOrder2(self, root):if not root: return []res = []pre_layer = [root]while pre_layer:cur_layer = []res.append([])for node in pre_layer:res[-1].append(node.val)cur_layer.extend(node.children)pre_layer = cur_layerreturn res

解法三

方法三：递归算法：我们可以使用递归来解决这个问题，通常我们不能使用递归进行广度优先搜索。这是因为广度优先搜索基于队列，而递归运行时使用堆栈，适合深度优先搜索。但是在本题中，我们可以以不同的顺序添加到最终列表中，只要我们知道节点在哪一层并确保在那一层的列表顺序正确就可以了。

def levelOrder3(self, root):def traverse(node, level):if len(res) == level:res.append([])res[level].append(node.val)for child in node.children:traverse(child, level + 1)res = []if root:traverse(root, 0)return res

解法四

首先判断root是否有内容，如果没有则输出[] 设置两个列表queue,res，前者存放节点，后者存放值开始循环，通过for循环将queue里面的值分离出来一次性加入res中， queue队列通过两个for循环，前面一个取出queue的节点，后一个将取出的节点再取子节点，然后得到queue 最后循环结束输出res

if not root: return []stack, res = [root], []while stack:res.append(node.val for node in stack)stack = [child for node in stack for child in node.children]return res