这门课是CS100.1x的后续课,看课程名字就知道这门课主要讲机器学习。难度也会比上一门课大一点。如果你对这门课感兴趣,可以看看我这篇博客,如果对PySpark感兴趣,可以看我分析作业的博客。
Course Software Setup
这门课的环境配置和上一门一模一样,参考我的这篇博客CS100.1x Introduction to Big Data with Apache Spark。
Lecture 1 Course Overview and Introduction to Machine Learning
这一章主要是背景介绍和一些基本概念的介绍。现在的数据越来越多,单一的机器处理这些数据的时候会很慢,所以产生了分布式计算,但是分布式计算本身很复杂,所以出现了Spark来简化分布式计算,特别是Spark MLlib,对解决机器学习问题非常好用。
紧接着介绍了机器学习的概念,包括机器学习的分类,机器学习的相关术语,机器学习的处理流程,处理垃圾邮件的具体例子,线性代数基础知识和衡量时间和空间复杂度的Big O。
这里每个内容都很广,所以不在这里赘述。有兴趣的可以搜搜其他博客。
Lecture 2 Big Data, Hardware Trends, and Apache Spark
这章内容和上一门课的lecture3和lecture4一模一样。参考我的这篇博客CS100.1x Introduction to Big Data with Apache Spark。
Lecture 3 Linear Regression and Distributed ML Principles
这一章干活很多。首先介绍了线性回归和最小二乘法,线性回归在工业中应用非常广,因为算法简单,效果好,而且可以通过增加特征来提高模型复杂度。当模型复杂度高时,容易过拟合,Rideg regression是个很好的选择。
这一章还给出了一个预测歌曲年代的例子,通过这个例子简单介绍了机器学习的处理流程。后面的作业会详细的解决这个问题。
这一章解释了如何用分布式来解决线性回归的问题。我们都知道,在解决线性回归的问题时,有一个closed form solution,如下图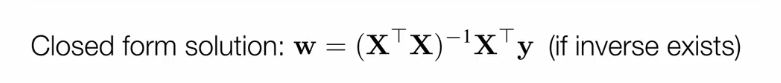
我们得到时间复杂度和空间复杂度
我们发现当数据量很大时,n一般很大,而d表示特征的多少,相比较n,显得很小。所以计算和存储的瓶颈就在于如何存储X和如何计算X的转置乘以X(原谅我懒得打公式)。因为这两项涉及到n。
第一个问题很好解决,因为我们这里就是讲分布式系统,直接把数据分布式存储就行。
第二个问题需要一些技巧,如下图,我们把矩阵的乘法从inner product变成outer product。

现在的时间和空间复杂度为
通过这些步骤,还有一个问题就是,时间和空间的复杂度里仍然有平方项,当d很大时,本地计算d*d也够呛。所以最好有一个复杂度为线性实现的方法。
第一个思路是利用数据的稀疏性,稀疏矩阵在实际问题中很常见,我们可以利用PCA降维,来把d变小;第二个思路就是换个算法,比如梯度下降。
梯度下降的定义和过程我们就不多说了,这里说说梯度下降在分布式里的应用和代码实现。

通过上面的步骤,也解释了三个经验法则。
Lecture 4 Logistic Regression and Click-through Rate Prediction
这一章主要讲逻辑回归和其应用——点击预测。点击预测主要用于在线广告,而且有很多难点,比如影响点击的因素太多太乱、数据量太大。然后介绍了监督学习的概念,并从线性回归到逻辑回归。然后介绍了FP,FN定义和用ROC plot来觉得阈值。接着介绍了如何处理类别型特征(label encoding和one-hot encoding)。当对特征这样处理后,整个矩阵可能会很稀疏,这时候用sparse representation会节省存储空间和计算量。
当one-hot encoding处理后特征太多时,最好不要丢特征,因为虽然矩阵很稀疏,不代表没有信息量;另外一个选择是用feature hashing。
Lecture 5 Principal Component Analysis and Neuroimaging
这一章主要讲PCA和神经科学。。我没太明白为什么讲神经科学,难道是和作业有关系么。然后介绍了无监督学习,从而引出了PCA。介绍PCA的博客太多了,这里不赘述。
这里重点讲讲PCA在分布式上的实现。分两种情况。
第一种情况是Big n和small d,分为4步。


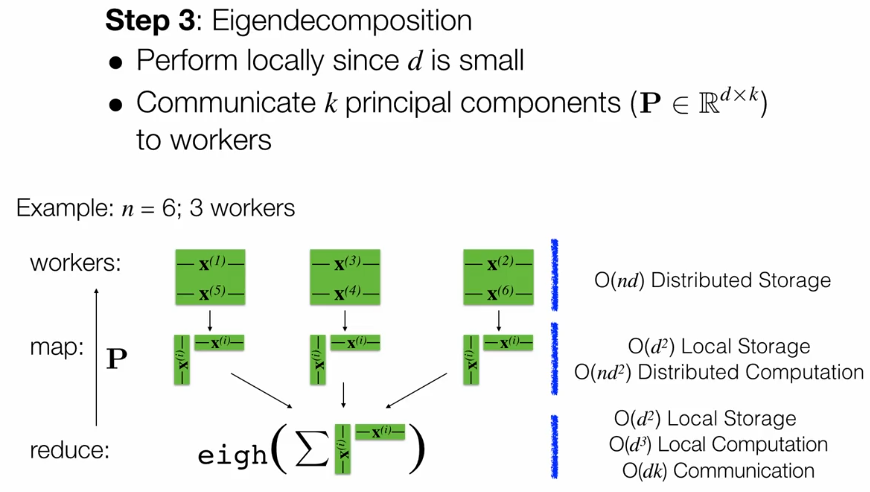
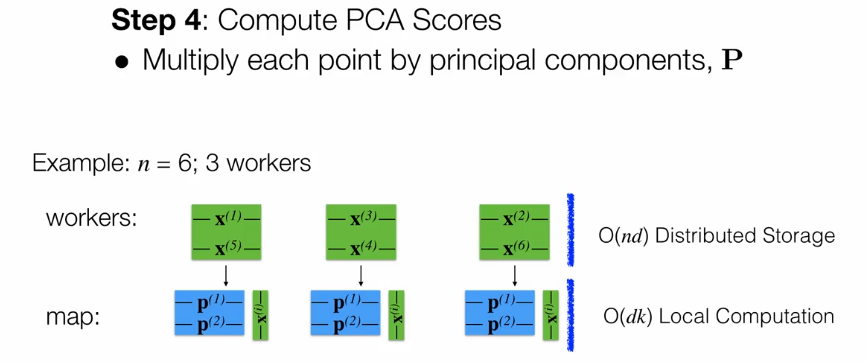
第二种情况是big n和big d。主要用迭代的方法。


)







 += test.o,这一类的是什么意思?)




)

![[LeetCode] [C++] 206 Reverse Linked List 反转单项链表](http://pic.xiahunao.cn/[LeetCode] [C++] 206 Reverse Linked List 反转单项链表)


---2017-04-24)
