哈夫曼编码的设计与应用
问题需求分析
用哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码(有时也称为霍夫曼编码)。
霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和，记为WPL=（W1L1+W2L2+W3L3+…+WnLn），N个权值Wi（i=1,2,…n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,…n）。
数据结构的定义
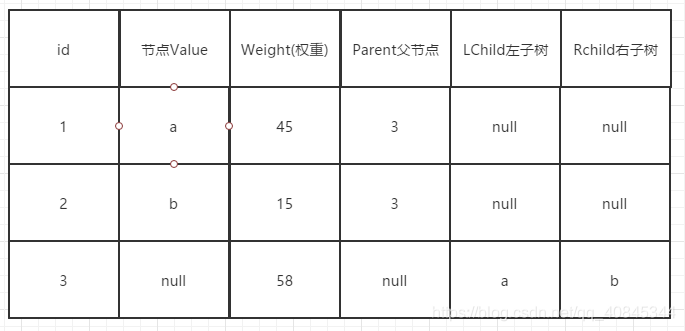
哈夫曼树结构体包含如下内容：节点权重，当前节点的父节点，左右子树，节点信息。
哈夫曼编码结构体包含如下内容：存编码的数组，编码数组的开始标志。
功能详细设计
构建哈夫曼树：使用一维数组，每个节点存储权重，父节点，左子树，右子树，以及数值的信息。遍历整个数组，根据每个节点的权重去找到最小以及第二小的节点，然后对各自的父节点，左右子树赋值，建立两个节点的联系将他们的联系填入该结构体数组中。
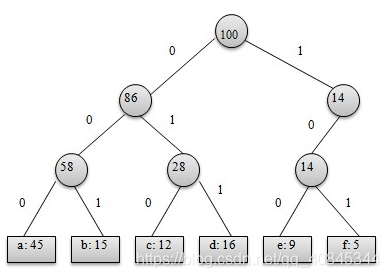
哈夫曼树如下图:
a权重45; b权重15; c权重12; d权重16; e权重9; f权重5
哈夫曼树结构体数组如下图(使用a, b, 58举例):
根据哈夫曼树建立哈夫曼编码：从树的根节点开始，根据每个叶子节点与父节点之间的联系，使用哈夫曼编码结构体中的编码数组储存树种每个叶子节点的编码, 往左边遍历是0, 往右边遍历是1, 举例: a, 由建立好的哈夫曼树可得, 当遍历查找到a的时候, a到root的路径是: 100->86->58->a, 所以可得编码就是000;
根据哈夫曼编码将指定的编码转化为字符串：读取到哈夫曼编码后，当编码为0表示节点是左子树，当编码为1的时候表示右子树，根据已经建立好的哈夫曼树，利用顺序遍历的方式，根据左0右1，寻找哈夫曼树中的叶子节点，当某一节点在哈夫曼树中左右子树都为空的时候，表示该节点即使叶子节点，然后输出对应叶子节点在哈夫曼编码数组中的位置, 其原理与编码的方式恰恰相符, 而是根据01数字查找对应的叶子节点.
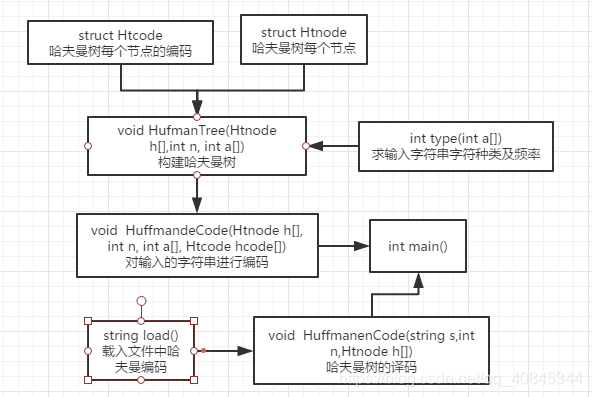
函数调用图:
编写代码体会
遇到的问题是数组下标没有弄好,导致建立哈夫曼树时出现各种错误, 进行编码过程没有将lchild与rchild的”变化写在一起”导致出现错误,其实最大的问题是:没有将代码的逻辑思路考虑清楚,还有边界条件值,最蠢的是没有打一下草稿,写一下伪代码,把程序的思想理解,导致编程的过程中出现各种问题,以后写代码之前还是把逻辑理清楚再动手写代码,最后再将代码写到电脑上测试。
完整代码
#include<iostream>
#include<string>
#include<fstream>
using namespace std;
struct Htnode{int weight,parent,lchild,rchild;char c;
};
struct Htcode{int bit[25],start;
};
int type(int a[]){string s;int sum = 0; cout<<"输入需要编码的字符串"<<endl;cin>>s;for(int i = 0; i < s.size(); i++){a[s[i]-'a']++;}cout<<"出现的字母种类以及频率:"<<endl; for(int i = 0; i < 26; i++){if(a[i] != 0){char c = char(i+'a');cout<<"i:"<<i<<" c:"<<c<<":"<<a[i]/(s.size()*1.0)<<endl;sum++; }}return sum;
}
//通过数组的方式构建哈夫曼树
void HufmanTree(Htnode h[],int n, int a[]){int i,j,max1,max2,x1,x2;for(i=0;i<2*n;i++){h[i].weight=0;h[i].parent=-1;h[i].lchild=-1;h[i].rchild=-1;h[i].c='\0';}for(i=0;i<26;i++){if(a[i] != 0){h[i].c = i + 'a';h[i].weight = a[i]; }}for(i=0;i<n-1;i++){max1=1000,max2=1000;x1=-1,x2=-1; for(j=0;j<n+i;j++){if(h[j].weight<max1 && h[j].parent==-1){max2=max1;x2=x1;max1=h[j].weight;x1=j;}else if(h[j].weight<max2 && h[j].parent==-1){max2=h[j].weight;x2=j;}}//根据每个节点信息, 将其信息存储到节点数组中h[x1].parent=n+i; h[x2].parent=n+i; h[n+i].weight=h[x1].weight+h[x2].weight;h[n+i].lchild=x1;h[n+i].rchild=x2;}for (i=0;i<2*n-1;i++){cout<<h[i].weight<<" "<<h[i].parent<<" "<<h[i].lchild<<" "<<h[i].rchild<<" "<<h[i].c<<endl; }
}
//哈夫曼编码
//根据叶子节点的位置, 将其path路径01数字填充到编码数组中
void HuffmandeCode(Htnode h[], int n, int a[], Htcode hcode[]){HufmanTree(h, n, a);ofstream out;out.open("HuffmandeCode.txt", ios::out);int i,j;for(i=0;i<n;i++){j=0;int parent=h[i].parent;//记录当前节点的父亲 int c=i;while(c!=-1){//parent造成根节点不会被访问 hcode[i].bit[j++]=h[parent].lchild==c?0:1;//从叶子节点到根节点, 应该使用栈结构 c=parent;parent=h[parent].parent;}hcode[i].start=j-1;}for(i=0;i<n;i++){cout<<h[i].c<<":";for(j=hcode[i].start-1;j>=0;j--){cout<<hcode[i].bit[j];out<<hcode[i].bit[j];}cout<<endl;}out.close();
}
string load(){ifstream in("HuffmandeCode.txt");string str;char buffer[256];if(!in.is_open()){cout<<"加载文件错误"<<endl; return NULL;} cout << "载入编码文件" << endl;in.getline(buffer, 100, ' ');return string(buffer);
}//哈夫曼译码
void HuffmanenCode(string s,int n,Htnode h[]){int i=0,j=0,lchild=2*n-2,rchild=2*n-2;while(s[i]!='\0'){if(s[i]=='0'){//出现的问题是,最初将lchild,rchild分开计算,导致在左右子树间相互变化出现//lchild,rchild不同同时表示同一个节点,最后想到lchild=rchild就能解决问题lchild=h[lchild].lchild;rchild=j=lchild;}if(s[i]=='1'){rchild=h[rchild].rchild;lchild=j=rchild;}if(h[lchild].lchild==-1 && h[rchild].rchild==-1){cout<<h[j].c;lchild=rchild=2*n-2;j=0;}i++;}
}
int main(){Htnode h[30];Htcode hcode[10];int a[26]={0};string s;int n = type(a);cout<<"n:"<<n<<endl;HuffmandeCode(h, n, a, hcode);HuffmanenCode(load(),n,h);return 0;
}
