自底向上分析之算符优先分析法
说明:以老师PPT为标准,借鉴部分教材内容,AlvinZH学习笔记。
基本过程
1. 一般方法:采用自左向右地扫描和分析输入串,从输入符号串开始,通过反复查找当前句型的句柄(最左简单短语),并利用有关规则进行规约。
分析过程如下,关键步骤是第一点!
- 找出当前句型的句柄 x (或句柄的变形);
- 找出以 x 为右部的规则 X::= x ;
- 把 x 规约为X,产生语法树的一枝。
2. 自底向上分析也叫作移进-规约分析,简单的例子中,识别句柄的过程,主要看栈顶符号串是否形成规则的右部。这种做法形式上正确,但实际上不一定正确。原因:不能认为对于句型xuy,若有U::=u,就断定u是简单短语或者u是句柄,也就是说这是一个必要不充分条件。
算符优先分析(OPP)
1. OPP:简单直观,广为使用的自底向上分析方法,易手工实现。可用于一大类上下文无关文法。
分析器的结构:符号栈、优先关系矩阵、分析程序。
2. 特点:预先规定相邻终结符之间的优先关系,利用优先关系确定句型的“句柄”并进行规约。
注意:
- 这里的“句柄”有可能不是真正的句柄,这种规约也未必是严格的最左规约。(后续解释)
- 对于二义性文法,如 \(E ::= E+E | E-E | E*E | E/E | (E) | i\),可以通过定义优先关系和左结合原则,OPP可分析之。
3. 终结符之间优先关系定义
- a = b:a的优先级等于b
- a < b:a的优先级小于b
- a > b:a的优先级大于b
注意: 这个关系是单方面的,也就是说这里的 “a<b” 并不意味着 “b>a”,同样的,“a=b” 也不意味着 “b=a”。
4. 优先关系举矩阵:左终结符(栈内)、右终结符(栈外),值为优先关系,空表示两个终结符不能相邻。
使用方法:当栈顶项(或次栈顶项) 终结符的优先级大于栈外的终结符的优先级则进行规约,否则移进。
出错情况:
- 相邻终结符之间无优先关系。
- 对双目运算符进行规约时,符号栈中无足够项。
- 非正常结束状态。
5. 优先函数:文法终结符之间的优先关系可以不用矩阵表示,而是采用两个邮箱函数来表示:f(x)表示栈内优先函数,g(x)表示栈外优先函数。把优先关系的比较转换成数值的比较。
特点:优先函数值不唯一,只要相互之间数值大小表示优先关系就行。
优点:节省内存空间,易于比较(数值比较)
缺点:可能掩盖错误,由于优先关系变为数值,原先可能不存在的优先关系现在也可比较了。可以通过特判避免这个问题。
OG与OPG定义
1. 算符文法(OG):若文法G中没有形如 \(U ::= ···VW···\) 的规则(V,W∈Vn),则称G为算符文法。
直观理解:算符文法不允许两个非终结符相邻!
2. 优先关系定义:设嗡文法G是一个OG文法,a,b∈Vt,U,V,W∈Vn。
a = b: iff 文法中有形如 \(U∷=…ab…\) 或 \(U∷=…aVb…\) 的规则。
a < b: iff 文法中有形如 \(U∷=…aW…\) 的规则,其中 \(W =+> b…\) 或 \(W =+> Vb…\)。
a > b: iff 文法中有形如 \(U∷=…Wb…\) 的规则,其中 \(W =+> …a\) 或 \(W =+>…aV\)。
TIP:只是定义,第二第三条实际用起来真的难用,还是继续看下去,用FIRSTVT和LASTVT高级操作吧!
3. 算符优先文法(OPG):设有一OG文法,如果在任意两个终结符之间,至多只有上述关系中的一种,则称该文法为算符优先文法(OPG)。
构造优先关系矩阵
1. 通过检查每一条规则,'=' 优先关系很容易求得,但是 '>' 和 '<' 就复杂了,需要引入两个集合辅助:FIRSTVT、LASTVT。
FIRSTVT( U ) = { b | U =+> b…或U =+> Vb…, b∈Vt , V∈Vn}
LASTVT( U ) = { a | U =+> …a 或U =+> …aV, a∈Vt , V∈Vn}
若文法有规则形如 \(W∷= ...a U...\),对任何 b∈FIRSTVT( U ),则有: a < b。
若文法有规则形如 \(W∷= ...U b...\),对任何 a∈LASTVT( U ),则有: a > b。
2.构造FIRSTVT集合
- 若有规则 U∷= b… 或 U∷= V b…,则 b∈FIRSTVT(U);
- 若有规则 U∷= V… 且 b∈FIRSTVT(V), 则 b∈FIRSTVT(U)。
3.构造LASTVT集合
- 若有规则 U::=…a 或 U::=…aV,则 a∈LASTVT(U);
- 若有规则 U::=…V,且 a∈LASTVT(V) ,则 a∈LASTVT(U)。
4.构造算符优先矩阵
FOR 每条规则U::= x1 x2…xn DOFOR i:=1 TO n-1 DOBEGINIF xi和xi+1均为终结符, THEN 置 xi=xi+1IF i≤n-2,且xi和xi+2都为终结符号但xi+1为非终结符号 THEN 置 xi=xi+2IF xi为终结符号xi+1为非终结符号 THENFOR FIRSTVT(xi+1)中的每个b DO 置xi<bIF xi为非终结符号xi+1为终结符号 THENFOR LASTVT(xi)中的每个a DO 置a>xi+1END5. 举个例子
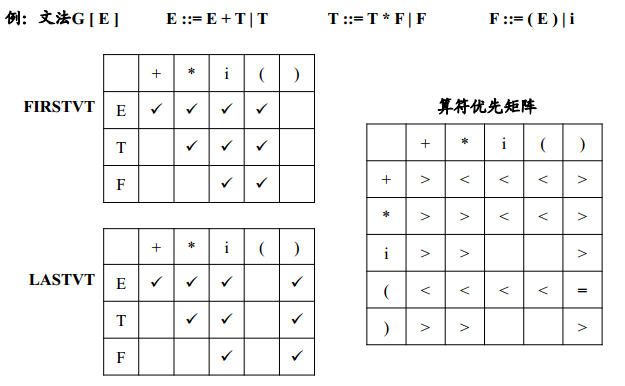
分析句子 \(i*(i+i)\)。

分析算符优先分析法
1. 提出问题:这种分析算法并不是严格的最左规约,也就是说,每次规约的未必是当前句型的句柄。那它规约的是什么?
答案:最左素短语。
先给出分析过程的特点(不予证明):
- 每次规约的最左子串,确实是当前句型的最左素短语;
- 规约的不都是真正的句柄(有时候是只是偶然);
- 没有完全按规则进行规约,因为素短语不一定是简单短语(有时候是只是偶然)
2. 素短语:句型的素短语是一个短语,它至少包含有一个终结符号,并且除它自身以外不再包含其它素短语。
例如:对于句型T+TF+i,通过语法树可以轻易找到所有短语:① T + T F + i;② T + T * F;③ T;④ T * F;⑤ i。①包含其它短语②包含其它短语③不包含终结符④是素短语⑤是素短语。最后最左素短语就是④T*F。然而该句型的句柄确实③T。
3. 形式化寻找最左素短语:设有OPG文法句型:#N1 a1 N2 a2…Nn an Nn+1 #,其中Ni为非终结符(可以为空),ai为终结符。
定理:一个OPG句型的最左素短语是满足下列条件的最左子串:Nj aj … Ni ai Ni+1,其中aj-1 < aj ,aj = a . . . . j+1 , aj+1 = aj+2 , … , ai-2 = ai-1 , ai-1 = ai, ai.> ai+1。
4. 实现算符优先分析法:找句型的最左子串(最左素短语)并进行规约。
具体实现:当栈内终结符的优先级<或=栈外终结符的优先级时,移进;当栈内终结符的优先级>栈外终结符的优先级时,表明找到了素短语的尾,再往前找其头,并进行规约。
引用说明
- 邵老师课堂PDF
- 《编译原理级编译程序构造》




)






)






