一、PCSS回顾

上一篇我们说了如何用PCSS是实现软阴影，这个过程是没有任何问题的，但是有一个速度的问题，因为PCSS涉及到非常多次对纹理特定某一块区域遍历的操作（工业界一般都是用在该区域采样的方式，会因此产生噪声，但是后续会再做图像空间降噪，包括时间累积和滤波），这节我们将讲解如何把比较慢的第一步的Blocker search和第三步的Percentage Closer Filtering变快。

二、VSSM/VSM—Variance Soft Shadow Mapping

1.VSSM的基本思想

VSSM就是为了针对性解决第一步和第三步速度慢的问题而提出的，先回忆一下我们在第三步干了什么，我们在Shadow map上一块区域内找有多少个texel上记录的深度是小于/大于该着色点的，然后得出一堆非0即1，再做(加权)平均。这里GAMES202里闫老师做了个类比，这个问题非常像你在一场考试中拿了多少分，而此时你想知道你排百分之几，而如果把所有的同学成绩都看一遍这就相当于我们前面PCSS所做的事情，这太慢了，所以我们想提出另外一种方法。

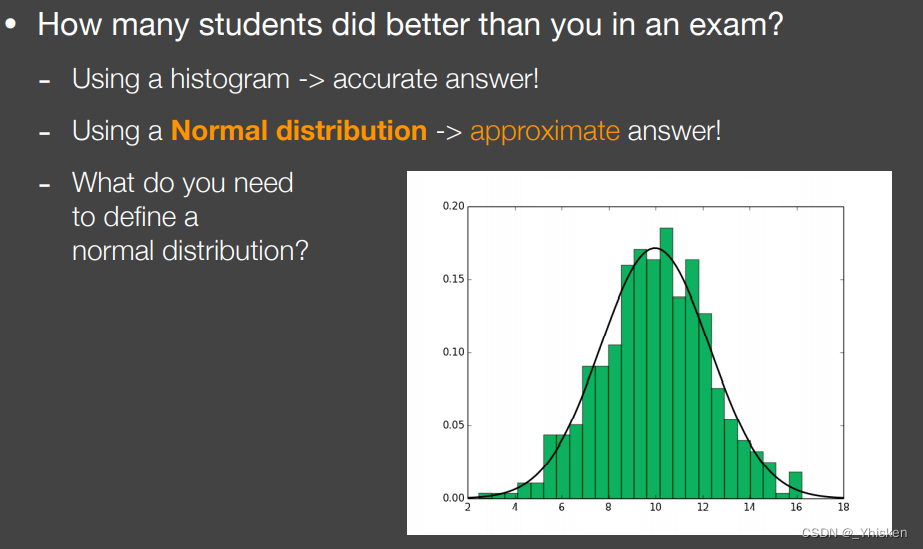
相对来说比较好的方法是如果我们有一个直方图，直方图又比较详细，那我们很轻易的就知道我们排百分之多少，那如果再不准一点呢？我们可以直接把它当成正态分布，这样我们直接就可以根据我们的成绩来估计我们排在前百分之多少了。

那么正态分布我们定义它的时候需要什么呢？只需要均值(期望)和方差即可。

也就是说VSSM的思想就是快速的计拿到范围内的均值和方差求出当前区域内深度的正态分布，以此来得出我们当前的着色点的深度在当前范围内的texel的深度中排名百分之多少。

而框出一片区域想快速得到均值这种方法我们在GAMES101中讲过，也就是Mipmap，但是我们需要注意Mipmap其实是不准的，而且只针对正方形。能够更精准的在2D上矩形中求均值的数据结构叫做Summed Area Tables，简称SAT。

至于方差，我们可以用概率论与统计中一个非常经典的公式来求得，如上图。但于此同时，我们需要在原本的Shadow Map基础上多记录一个通道，它用来储存深度的平方。(我们不需要多生成一张Texture记录深度的平方，只需要在RGB三个通道中多一个通道顺手记录深度平方即可)

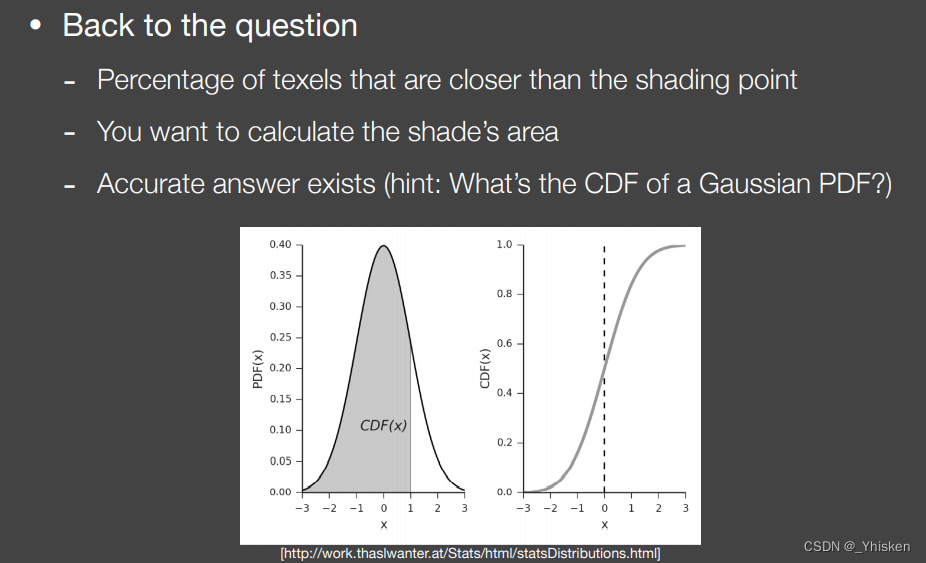
而事实上在概率论中，我们想求得东西也就是上图中阴影区域的面积，也就是CDF。CDF(x)代表了有多少值小于x，也就是上图中右边的曲线。至于如何求出这个面积，可以通过高斯分布的查表或者error function的解析解，但我们这里不采用这种形式因为很麻烦，VSSM采用了切比雪夫不等式来近似。

2.切比雪夫不等式—Chebychev’s inequality

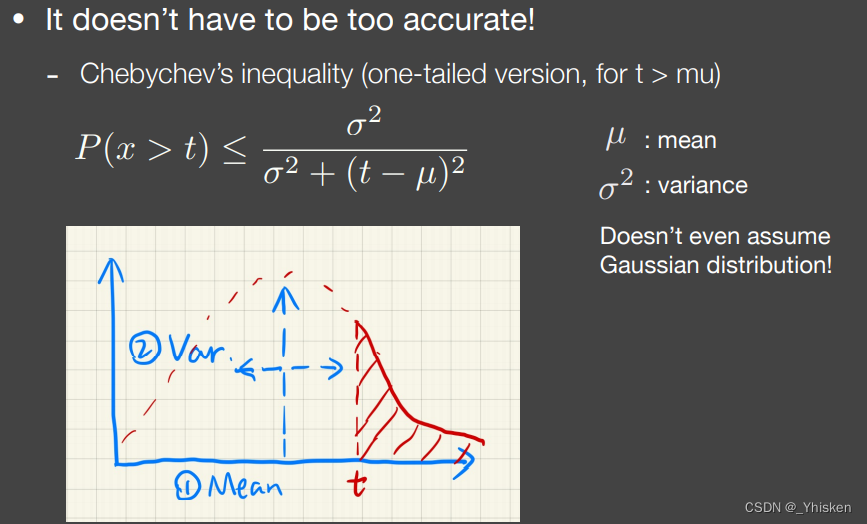
切比雪夫不等式可以在我们不知道随机变量满足的分布是什么样子的情况下，告诉我们一个随机变量超过某一个值的概率，它只需要知道这个分布的期望和方差即可。如上图，我们不知道上图的分布具体信息，但是我们知道它的方差和期望，如果真的给了我们一个值t(t值必须大于均值)，我们通过不等式可以知道随机变量大于t的概率，也就是上图中红色的面积不会超过不等式右边那一大堆东西。同时上一篇我们提到，在实时渲染中，我们通常会把不等式当成约等式使用，也就是说切比雪夫不等式在这里给了我们对这片红色面积的一个不错的估计。

因此我们就可以用更简便的方法计算上面提到的CDF。实际上VSSM在实际操作过程中由于切比雪夫不等式的缘故，故根本不涉及到正态分布以及任何其它分布的定义和计算。

3.回到Blocker search

解决完了第三步我们再回头看第一步的操作，在第一步也就是Blocker search中我们对比区域内的所有texel的深度z和着色点的深度t，如果z<t，则该texel为遮挡物，否则则不是，然后计算遮挡物的平均深度Zocc和非遮挡物的平均深度Zunocc。但显然这太慢了。

我们观察一下上面的等式，很容易理解，因为非遮挡物的比例+遮挡物的比例=1。我们最终的目的是知道Zocc，N我们知道，Zavg我们由SAT或Mipmap也可以很快拿到，N1可以由前面提到的切比雪夫不等式得到，N2则为1-N1，那么只剩下了Zunocc，那么Zunocc怎么得到呢？

这里VSSM做了个更大胆的假设，Zunocc就等于t，也就是上面红色数字的平均深度值就假设为着色点的深度。当然这个假设过后，如果接受阴影的不是平面或者阴影接收面和光源不平行的时候就会出现一些问题。

4.SAT—Summed Area Tables

给定矩形范围内的查询，我们最先想到的是GAMES101里面提到的Mipmap，但是它的特性是近似，快速，正方形 ，也就有局限性，近似代表不准确，并且层与层之间要进行插值，而正方形则是自身限制。

因为Mipmap范围查询的诸多问题，我们提出一种新的数据结构来进行精确的范围查询，也就是SAT。SAT和前缀和算法是紧密结合的。并且由于范围求平均和范围内求平均是一样的，我们只需要快速求和即可。

看上图中的一维数组，蓝色数组是我们查询的对象，如图如果我们正常求上面的sum，那么时间复杂度是O(n)，我们想避免它。于是我们使用了SAT，SAT实际上就是一次预计算的处理，我们在数组之外生成的SAT每个SAT的第n个元素记录数组前n个元素的和。而此时，当我们想求sum的时候，只需要用SAT[5]减去SAT[2]就可以了。

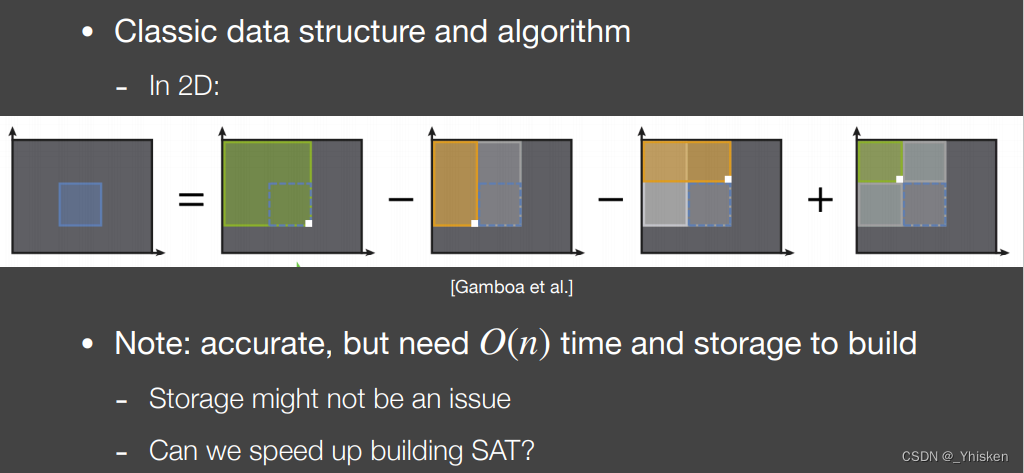
理解了一维我们再来看二维，如图如果我们要查询上图中蓝色区域的和，那么如图所示步骤，我们可以通过最左上角坐标和蓝色方形右下角的点组成绿色大方形，然后减去两个橙色方形，而因为多减了一个小方形，我们最后再加一个小的方形就可以得到蓝色区域内的和了。

橙色方形和小绿色方形的坐标都可以由左上角坐标和蓝色方形的右下，右上，左上角坐标得到。

这样我们看到我们只需查询4次SAT就可以得到任意一块矩形区域内数值的和了。同时因为GPU的并行度行列计算并行，构建SAT的时间复杂度O(m*n)可以一定程度减小。

5.VSSM的问题

1.分布假设问题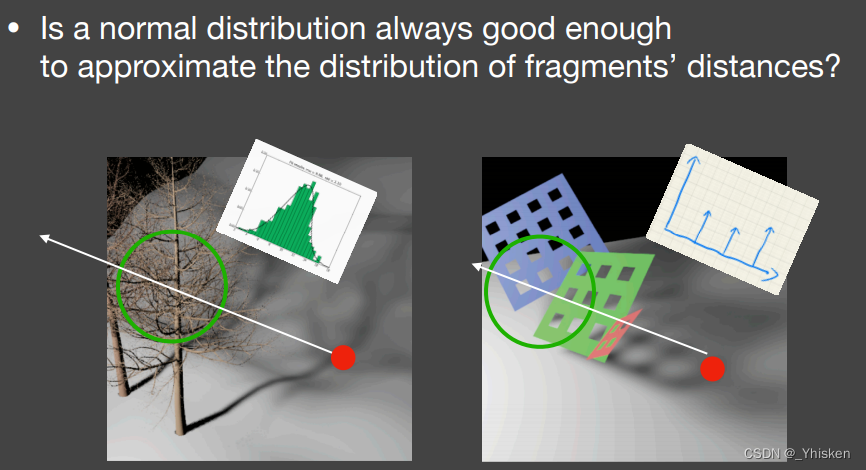

我们之前说过使用切比雪夫不等式的时候也好还是最开始假设的时候也好，我们都假设遮挡关系符合一个类似正态分布，但实际上如果是上图中右图的情况，反而不能这样假设，而它的分布是尖锐的峰值。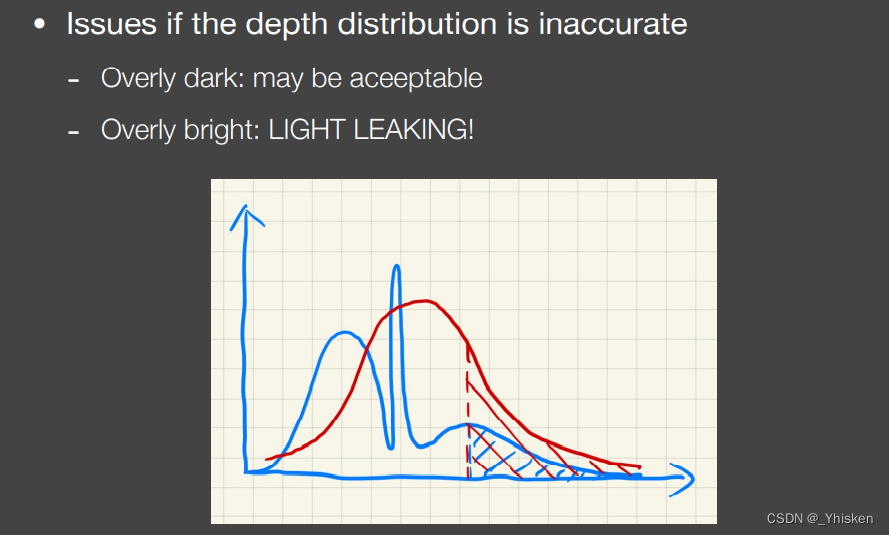

同时，在某些情况，因为分布估计不仅可能完全准确符合实际分布，实际计算出的阴影可能在某些地方突然变黑，但这种情况人们可以一定程度上接受，但人们无法接受有时因为分布估计的误差导致阴影突然变白，也就是漏光，如下图的车子阴影。

2.阴影接收物非平面 

其次是阴影接收物不是平面的问题，因为我们在Blocker search的时候把Zunocc直接当成了着色点的深度t，因此非平面会导致阴影断裂如上图的蓝黄色的平面渲染图。

3.切比雪夫不等式自身局限

其次，切比雪夫不等式自己的问题，我们的着色点深度t必须大于分布的期望值。

 

三、MSM—Moment Shadow Mapping

Moment Shadow Mapping只解决了我们VSSM中的第一个问题，也就是深度值分布描述不准的问题，它采用的方法是使用更高阶的Moments，也就是更高阶的矩。

这里的矩简单理解，我们记录一个数的1次方，2次方，3次方，最后记录到几次方就是保留了前几阶的矩。

我们回忆VSSM干了什么事，我们只采用了前两阶的矩，然后来计算它的方差。由此我们想到，那自然阶数越多，得到的越准确。

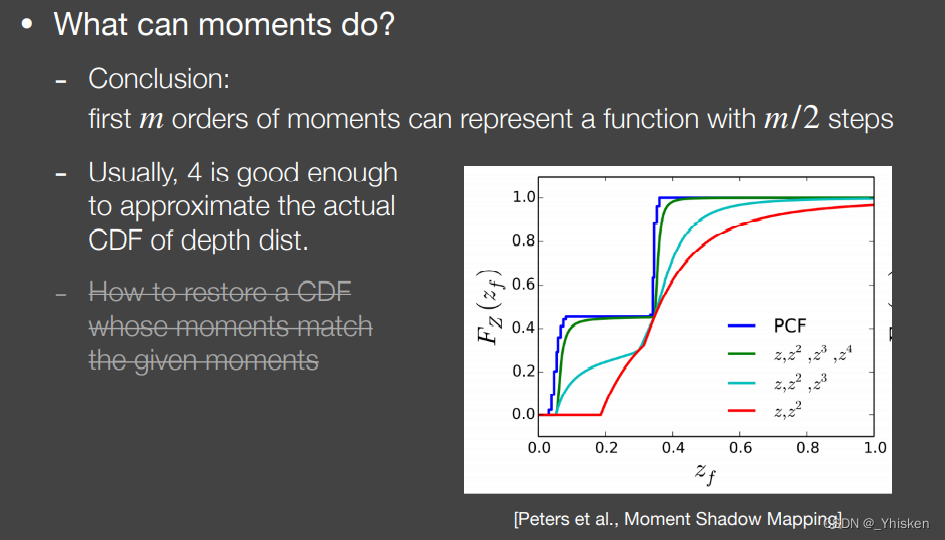
如果保留前m阶的矩，我们就可以表示一个由一系列阶跃函数组成的函数，并且可以表示的台阶为m/2个台阶，如上图中深绿色的函数，保留了4阶矩，于是有两个台阶，于是就可以更好的还原蓝色的线，也就是CDF，类似于某种展开。正常情况下，用四阶的矩已经足够了。

至于如何根据前四阶的矩，我们怎么得到这条绿色的线，这是非常非常复杂的，这里就不说了，有兴趣的朋友自行搜索。

在工业界中有一些存储的小细节，比如4阶的矩，我们如果想用float32存储，可以把float32拆成四个8位的来存储，也就是packing打包，使用的时候再解包也就是unpacking，只不过这样做了之后我们就无法插值了。

最后可以看到，MSM的效果比VSSM效果好很多，没有漏光现象，如上图。

参考

Lecture4 Real-time Shadows 2_哔哩哔哩_bilibili

GAMES202_Lecture_04 (ucsb.edu)